A 2000 februári A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 230. Határozzuk meg azokat az a egész számokat, amelyekre

(1)    

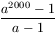
négyzetszám.

Megoldásvázlat. Ha a<-1, akkor (1) negatív, tehát nem lehet négyzetszám. Ha a=-1 vagy a=0, akkor (1) értéke 0 illetve 1, vagyis négyzetszám. Ha a=1, akkor a nevező 0, és (1) nem értelmes. A továbbiakban feltételezzük, hogy a2.

A három tényezőt rendre A, B, C-vel jelölve B és C osztója A-2=(a¹⁰⁰⁰-1)-nek, továbbá C osztója B-2=(a⁵⁰⁰-1)-nek. Ebből következik, hogy az A, B és C közül bármelyik kettő legnagyobb közös osztója legfeljebb 2.

Három ilyen szám szorzata csak úgy lehet négyzetszám, ha külön-külön is mindegyikük négyzetszám vagy négyzetszám kétszerese. Az A és a B éppen 1-gyel nagyobbak az a¹⁰⁰⁰ illetve a⁵⁰⁰ pozitív négyzetszámoknál, ezért nem lehetnek négyzetszámok.

Ha A és B is egy-egy négyzetszám kétszerese, akkor 4AB=4a¹⁵⁰⁰+4a¹⁰⁰⁰+4a⁵⁰⁰+4 négyzetszám. Ez azonban ellentmondás, mert

4a¹⁵⁰⁰+4a¹⁰⁰⁰+4a⁵⁰⁰+4>4a¹⁵⁰⁰+4a¹⁰⁰⁰+a⁵⁰⁰=(2a⁷⁵⁰+a²⁵⁰)²

és

4a¹⁵⁰⁰+4a¹⁰⁰⁰+4a⁵⁰⁰+4<4a¹⁵⁰⁰+4a¹⁰⁰⁰+4a⁷⁵⁰+a⁵⁰⁰+2a²⁵⁰+1=(2a⁷⁵⁰+a²⁵⁰+1)²,

vagyis 4AB is két szomszédos négyzetszám közé esik.

Az a>1 esetben tehát (1) nem lehet négyzetszám. Összesen két megoldás van tehát: a=-1 és a=0.

Több dolgozat alapján

Megjegyzés. Azt, hogy a¹⁰⁰⁰+1 és a⁵⁰⁰+1 nem lehet egyszerre egy-egy négyzetszám kétszerese, másképpen is bizonyíthatjuk. Tegyük fel, hogy a¹⁰⁰⁰+1=2x² és a⁵⁰⁰+1=2y². Ekkor

Mivel egész számokról van szó, ebből következik, hogy

Négyzetre emelés és rendezés azt kapjuk, hogy a⁵⁰⁰<<0.

Varjú Péter 11. o. (Szeged, Radnóti M. Gimn.)

A. 231. Bizonyítsuk be, hogy ha egy összefüggő egyszerű gráfban minden csúcs foka legalább 3, akkor tartalmaz olyan kört, amelynek éleit elhagyva a gráf összefüggő marad.

Javasolta: Kiss Tamás, Budapest

Megoldásvázlat. A következő, erősebb állítást bizonyítjuk be.

Ha egy összefüggő egyszerű gráfban minden csúcs foka legalább 3, és egy tetszőleges éle pirosra van festve, akkor a gráf tartalmaz olyan kört, amelyet elhagyva a gráf összefüggő marad, és a kör nem tartalmazza a pirosra festett élt.

Először minden 3-nál magasabb fokú csúcsot cseréljünk ki kisebb fokszámú csúcsokra:

Ezután a gráfnak mindegyik csúcsa pontosan harmadfokú lesz. Azt is feltételezhetjük, hogy a piros él legalább egy körnek éle. Ha nem lenne, akkor színezzük ki helyette egy kör valamelyik élét pirosra. (Mivel minden pont foka legalább 2, a gráf tartalmaz kört.)

A bizonyítás további részét a csúcsok száma szerinti teljes indukcióval végezzük. Ha a gráfnak csak 4 pontja van (kevesebb nem lehet), akkor az a teljes 4-pontú gráf, ebből két olyan háromszög is kiválasztható, amelyik nem tartalmazza a piros élt.

Ha a gráfnak 4-nél több csúcsa van, akkor a következő eseteket vizsgáljuk.

I. eset. A gráfban van 4 pont, amelyek két, élben szomszédos háromszög csúcsai, és a piros él ezek egyikéből indul ki.

Ha a két további szomszédos pont különböző és nincs közöttük él, akkor a háromszögeket alkotó 4 pontot és 7 élt kicserélhetjök egyetlen piros élre:

Az így kapott gráf az indukciós feltevés szerint tartalmaz egy kört, amit elhagyva a gráf összefüggő marad, és ez a kör nem tartalmazza az új piros élt. A kör az eredeti gráfban is megfelelő lesz.

Ha a két szomszédos pont egybeesik vagy él fut közöttük, akkor a két háromszög valamelyikét elhagyva a gráf összefüggő marad. Ezért csak azt az esetet kell megvizsgálnunk, amikor a piros él a két háromszög közös éle:

II. eset. Van olyan háromszög, aminek egyik csúcsából indul ki a piros él, de ez a háromszög nem szomszédos más háromszöggel.

A háromszög csúcsainak még egy-egy, egymástól különböző szomszédja van. Ebben az esetben húzzuk össze a háromszöget egyetlen ponttá:

III. eset. A gráf nem tartalmaz olyan háromszöget, aminek van közös éle a piros éllel.

A piros él két végpontjának 4 különböző szomszédja van. Ebben az esetben a következő egyszerűsítést hajtsuk végre:

(A gráf összefüggő marad, mert a piros él legalább egy körnek éle.)

A kapott, kevesebb csúcsú gráfban van olyan kör, amit elhagyva az összefüggőség megmarad, és a kör nem tartalmazza a piros élt. Könnyen ellenőrizhető, hogy ebből a körből egy megfelelő kör nyerhető az eredeti gráfban is.

A. 232. Mutassunk példát olyan konvex poliéderre, amelynek legalább 2000 csúcsa van, nincs 1/2-nél rövidebb éle, ugyanakkor belefér egy egységnyi sugarú gömbbe.

Megoldásvázlat. Legyen A=(0;0;0), B=(;0;0). Legyen továbbá tetszőleges 1n2000 páratlan egész szám esetén C_n=(;x_n;y_n), páros n esetén pedig C_n=(1;x_n;y_n), ahol az x₁, ..., x₂₀₀₀ és y₁, ..., y₂₀₀₀ számokat később definiáljuk.

A cél egy olyan konvex test konstruálása, amelynek lapjai az ABC₁ és ABC₂₀₀₀, valamint az AC_2n-1C_2n (n=1,2,...,1000) és BC_2nC_2n+1 (n=1,2,999) háromszögek.

Ha az x₁, ..., x₂₀₀₀ számokat úgy választjuk, hogy x_n+1<x_n legyen, akkor a pontok vetületei az x-y síkra az ábrán látható módon helyezkednek el, tehát C_n+1 vetülete az ABC_n háromszög vetületének belsejébe esik. A továbbiakban legyen

x_n= ()ⁿ.

Egy kis számolással ellenőrizhető, hogy a z-tengely pozitív irányából nézve

A C_nC_n+1 él akkor konvex, ha y_n+1<y_n;

Páratlan n-re az AC_n+1, páros n-re a BC_n+1 él akkor konvex, ha y_n+1<y_n+y_n+2;

Páros n-re az AC_n+1, páratlan n-re a BC_n+1 él akkor konvex, ha y_n+1<y_n+y_n+2.

Mindezek teljesülnek az

y_n= ()ⁿ

választással.

A megadott test belefér az ABC₁ háromszög köré írt gömbbe, amelynek sugara kisebb, mint 1 egység. Minden él hossza legalább , mert a csúcsok az y=0, y= y=1 és y= síkokban helyezkednek el, és egyik síkon belül sincs éle a testnek.