Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A 2000. februári B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaLban folyamatosan közöljük.

B. 3342. Határozzuk meg azokat a pozitív egész számokat, amelyekre n2-19n-99 négyzetszám. (3 pont)

Amerikai feladat

Megoldásvázlat. Legyen n2-19n-99=x2, ahol x nemneagtív egész szám.

4n2-76n+361-4x2=757;

(2n-19-2x)(2n-19+2x)=757.

A 757 prímszám. Mivel a második tényező nagyobb az elsőnél, két eset lehetséges:

a) 2n-19-2x=1 és 2n-19+2x=757. Ezt az egyenletrendszert megoldva n=199 és x=189.

b) 2n-19-2x=-757 és 2n-19+2x=-1. Ebben az esetben n=-180 és x=189 adódik, ami nem megoldás.

B. 3343. Az ABC háromszög AB oldalának felezőpontja F. Az AFC háromszög súlypontja S1, a BFC háromszög súlypontja S2. Az AS1 egyenes a BC oldalt a P1 pontban, a BS2 egyenes az AC oldalt a P2 pontban metszi. Igazoljuk, hogy az S1S2P1P2 négyszög paralelogramma. (3 pont)

Megoldásvázlat. Legyen a CF szakasz felezőpontja G, az AC szakaszé H. Az AFC háromszögben az AG és FH szakaszok súlyvonalak, tehát átmennek az S1 súlyponton. Továbbá az AS1 egyenes azonos az AG súlyvonallal, tehát P1 is erre az egyenesre illeszkedik.

Az ABC háromszögben FH a BC oldalhoz tartozó középvonal, tehát párhuzamos BC-vel. Az FP1G CS1G háromzögek egybevágóak, mert megfelelő oldalaik egy egyenesre illeszkednek illetve párhuzamosak, továbbá FG=CG. Ebből következik, hogy P1G= S1G.

Hasonlóan kapjuk, hogy P2G= S2G. Az S1S2P1P2 négyszög S1P1 és S2P2 átlói a G pontban felezik egymást, tehát a négyszög paralelogramma.

B. 3344. Tekintsük azokat a természetes számokat, amelyek osztóinak számát megkapjuk úgy, hogy a prímtényezős felbontásukban szereplő prímszámok szorzatából kivonjuk a hatványkitevők szorzatát. Ilyen például a 25 és a 600 is. Bizonyítsuk be, hogy végtelen sok ilyen szám van. (4 pont)

Megoldásvázlat. Tetszőleges p prímszámra a p(p-1)/2 szám ilyen.

B. 3345. Egy egyfordulós, körmérkőzéses focibajnokságon 9 csapat indult. Az Alsórákosi STC csapata 5 győzelmet aratott és 3 vereséget szenvedett. Lehetséges-e, hogy ezek után a csapat csak 7. lett? (A győzelemért 3, a döntetlenért 1-1 pont jár, azonos pontszám esetén a sorrendet a gólkülönbség dönti el.) (4 pont)

Megoldásvázlat. Lehetséges. Számozzuk meg a csapatokat 1-től 9-ig. Tegyük fel, hogy az 1-7. csapatok midegyike nyer a 8. és 9. csapatok ellen, így ez a két csapat lesz a két utolsó helyezett.

Az első 7 csapat között történjenek a következő körbeverések: 12345671, 13572461, 14736251. Ezáltal az 1-7. csapatok mindegyike 5-ször győz, 3-szor veszít, és csak a gólkülönbség dönt közöttük.

B. 3346. Száz darab súlyt, melyek egyenként rendre 1, 2, ..., 100 gramm tömegűek, úgy helyeztünk el egy kétkarú mérleg két serpenyőjébe, hogy a mérleg egyensúlyban van. Bizonyítsuk be, hogy a serpenyőkből elvehetünk két-két súlyt úgy, hogy a mérleg továbbra is egyensúlyban maradjon. (5 pont)

Tournament of Towns, 1999.

Megoldásvázlat. A súlyok összege 5050 gramm, tehát 2525 gramm van egy serpenyőben. Feltehetjük, hogy az 1 grammos súly a bal serpenyőben van. Legyen a jobb serpenyőben található legkisebb súly n grammos. Mivel az első 71 pozitív egész összege nagyobb, mint 2525, ezért n71. Így létezik n+1 és n+2 grammos súly is.

1. eset: Az n+1 grammos súly a jobb serpenyőben van. Ha a bal serpenyőben nincs más súly, csak az 1, 2, ..., n-1 grammos, akkor ezek összege n(n-1)/2 gramm. Ez n71 esetén legfeljebb 2485 gramm. Tehát kell, hogy legyen még súly a bal serpenyőben. Legyen ezek közül a legkisebb i grammos.

Az i-1 grammos súly a jobb serpenyőben van. Így a bal serpenyőből az n-1 és az i, a jobb serpenyőből pedig az n és az i-1 grammos súlyt elvéve a mérleg egyensúlyban marad. (Az n és az i-1 grammos súly nem ugyanaz, mert i>n+1.)

2. eset: Az n+1 grammos és az n+2 grammos súly is a bal serpenyőben van. Legyen a jobb serpenyőben a második legkisebb súly m grammos. Mivel m>n+2, az m-1 grammos súly a bal serpenyőben van.

Ekkor m-1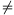n+1, mindkettő a bal serpenyőben van, és összsúlyuk megegyezik a jobb serpenyőben található m grammos és n grammos súlyok összsúlyával, tehát ezt a két-két súlyt elvéve, a mérleg egyensúlyban marad.

3. eset: Az n+1 grammos súly a bal, az n+2 grammos súly pedig a jobb serpenyőben van. Ha a bal serpenyőben nincs más súly, csak az 1, 2, ..., n-1 és az n+1 grammos, akkor ezek összege n(n+1)/2+1 gramm. Ez n70 esetén legfeljebb 2486 gramm, n=71 esetén pedig 2557 gramm. Tehát kell, hogy legyen még súly a bal serpenyőben. Legyen ezek közül a legkisebb k grammos. Mivel ez nem lehet az n+2 grammos súly, ezért a k-1 grammos súly a jobb serpenyőben van.

Így a bal serpenyőből az n-1 és a k, a jobb serpenyőből pedig az n és a k-1 grammos súlyokat elvéve a mérleg egyensúlyban marad.

Csóka Endre dolgozata alapján

B. 3347.  Tekintsünk egy négyszöget     (a) a csúcsaiból álló pontnégyesnek;(b) homogén lemeznek. Milyen négyszögek esetén esik egybe a kétféle alakzat súlypontja? (4 pont)

Javasolta: Bogdán Zoltán, Cegléd

Megoldásvázlat. Felhasználjuk a Bogdán Zoltán Megjegyzés a B. 3295. feladathoz - alakzatok súlypontjáról c. cikkében (KöMaL, 2000. februári szám) közölt eredményeket.

Ha az ABCD homogén négyszöglemezt az AC átlójával két háromszögre bontunk, akkor a négyszöglemez súlypontja rajta van a háromszöglemezek súlypontját összekötő szakaszon. Legyen az AC szakasz felezőpontja O, az ABC és ACD háromszögek súlypontjai SB illetve SD, az AC szakasz messe BD-t és SBSD-t az M illetve N pontokban.

Ezen kívül jelöljük mindegyik pont O-ból indított helyvektorát a megfelelő vastag kisbetűvel.

A négy csúcspont S súlypontjának helyvektora

s=(a+b+c+d)=(b+d)=m+x(d-b),

ahol x alkalmas valós szám.

A homogén négyszög H súlypontja a BD-vel párhuzamos SBSD szakaszon van, ezért helyvektora

h=n+y(d-b)=m+y(d-b),

ahol y alkalmas valós szám. Az s és h vektorok akkor egyenlők, ha m=0 és x=y. (Ez megfordítva is igaz: ha m=0, akkor az S pont az SBSD egyenesre esik.) Az m=0 feltétel azt jelenti, hogy az BD átló felezi az AC átlót.

Hasonlóan kapjuk, hogy az AC átló is felezi a BC átlót. Az ABCD négyszög tehát paralelogramma. A paralelogrammák súlypontja viszont mindkét értelemben a középpont.

Azok a négyszögek tehát, amelyek súlypontja a kétféle értelemben egybeesik: a paralelogrammák.

B. 3348. Határozzuk meg az

(1)    

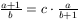
egyenlet egész megoldásait. (4 pont)

Javasolta: Fried Ervin, Budapest

Megoldásvázlat. Az egyenlet nem értelmes, ha b értéke 0 vagy -1. Az is könnyen ellenőrizhető, hogy a nem lehet 0.

Az egyenletből kifejezve c-t,

;

a jobb oldalon mindkét tényező 0 és 2 közé esik, ezért 0c4.

  • Ha c=4, akkor 1/a és 1/b értéke is 1, azaz a=b=1.

  • Ha c=0, akkor (1) jobb oldalán 0 áll, ezért a=-1, b pedig tetszőleges szám lehet a 0 és a -1 kivételével.

  • Ha c=1, akkor az egyenletet beszorozva kapjuk, hogy a+b=-1.

  • Ha c értéke 2 vagy 3, akkor írjuk át (1)-et a következő alakba:

    (c-1)ab-a-b=1

    (c-1)2ab-(c-1)a-(c-1)b+1=c

    ((c-1)a-1)((c-1)b-1)=c.

    A c=2 esetben (a-1)(b-1)=2. A 2 négyféleképpen alakítható szorzattá, ezekből az (2,3), (3,2), (0,-1) és (-1,0) számpárokat kapjuk; az utóbbi kettő nem megoldás.

    A c=3 esetben (2a-1)(2b-1)=3. A 3 négyféleképpen alakítható szorzattá, ezekből az (1,2), (2,1), (0,-1) és (-1,0) számpárokat kapjuk; az utóbbi kettő ismét csak nem megoldás.

    Az összes megoldást összefoglaltuk a következő táblázatban:

    abc
    -1tetszőleges, kivéve 0, -10
    -1-btetszőleges, kivéve 0, -11
    232
    322
    123
    213
    114

    B. 3349. Mutassuk meg, hogy a pp=qq egyenletnek végtelen sok olyan pozitív racionális megoldása létezik, ahol p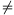q. (5 pont)

    Javasolta: Lóczi Lajos, Budapest

    Megoldásvázlat. Lóczi Lajos Mikor kommutatív, illetve asszociatív a hatványozás? c. cikkében (KöMaL, 2000. januári szám) olvashatjuk, hogy végtelen sok olyan racionális x,y számpár van, amelyre x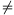y és xy=yx. Minden ilyen számpárból egy megfelelő p,q számpárt kapunk a p=1/x, q=1/y választással.

    B. 3350. Adott egy téglatest és a belsejében egy P pont. Tükrözzük P-t a téglatest minden lapjára. A hat tükörkép által meghatározott konvex test térfogata a P pont mely helyzetében lesz a legnagyobb? (3 pont)

    Megoldásvázlat. Legyenek a téglatest élei a,b,c; a P pont távolságai a lapoktól x és a-x, y és b-y, iletve z és c-z.

    A P tükörképei által meghatározott test csúcsait jelöljük az ábra szerint.

    A Q1R1Q2R2 négyszög területét a PQ1R1, PR1Q2, PQ2R2 és PR2Q1 derékszögű háromszögek területének összegeként számíthatjuk ki:

    t(Q1R1Q2R2)= 2x.2y/2+ 2y.2(a-x)/2+ 2(a-x).2(b-y)/2+ 2(b-y).2x/2=2ab.

    A teljes test térfogata pedig a Q1R1Q2R2S1 és Q1R1Q2R2S2 gúlák térfogatának összege:

    V(Q1Q2R1R2S1S2) = V(Q1R1Q2R2S1)+V(Q1R1Q2R2S2) = 2ab.2z/3+2ab.2(c-z)/3 = 4abc/3.

    A P pont tükörképei által meghatározott test térfogata tehát 4abc/3, függetlenül a P megválasztásától.

    B. 3351. Adott a térben legalább négy körvonal úgy, hogy középpontjaik közül semelyik 4 nincs egy síkban. Igaz-e, hogy ha bármely két körvonalhoz létezik őket tartalmazó gömbfelület, akkor létezik olyan gömbfelület is, amelyik mindegyik körvonalat tartalmazza? (5 pont)

    Megoldásvázlat. Bebizonyítjuk, hogy az állítás igaz.

    Legyenek a körvonalak k1, ..., kn. Jelöljük ti-vel ki tengelyét (azt az egyenest, amely áthalad kn középpontján és merőleges annak síkjára).

    Legyen most i és j két különböző index, és tekintsük most azt a gömböt, amely illeszkedik a ki és kj körökre. Ennek középpontja illeszkedik a ti és tj egyenesekre, tehát ennek a két egyenesnek van közös pontja; vagy egybeesnek, vagy metszik egymást. Tehát bármely két tengely vagy egybeesik, vagy metszi egymást.

    Ha az összes tengely egy síkban lenne, akkor ez a sík tartalmazná az összes kör középpontját is. Ezért a tengelyek nem esnek egy síkba. Ebből először is következik, hogy vannak közöttük különbözők. A szimmetria miatt feltehetjük, hogy t1 és t2 különbözők; ezek az előbbiek szerint metszik egymást. Másodszor, van olyan tengely, ami nincs benne t1 és t2 síkjában; legyen t3 egy ilyen. Ekkor a t1, t2, t3 egyenesek közül bármelyik kettő metszi egymást, de a három egyenes nincs egy síkban; ez csak úgy lehetséges, ha egy ponton mennek át.

    Legyen a t1, t2, t3 egyenesek közös pontja C. Annak a gömbnek a középpontja, ami illeszkedik a k1 és k2 körökre, csak C lehet, mert rajta kell lennie mindkét kör tengelyén. A középpoint tehát C, és így C egyenlő távolságra van a k1 és k2 körök pontjaitól. Hasonlóan kapjuk, hogy C ugyanilyen távolságra van a k3 kör pontjaitól; jelöljük ezt a távolságot R-rel.

    A továbbiakban megmutatjuk, hogy mindegyik körvonal illeszkedik a C középpontú, R sugarú gömbfelületre. Ezt a k1, k2, k3 körökről már tudjuk. Tekintsünk egy tetszőleges további ki kört. A ti tengely egy síkban van a t1, t2, t3 tengelyek közül bármelyikkel; ez csak úgy lehetséges, ha átmegy C-n. A ti legalább kettőt metsz a t1, t2, t3 egyenesek közül (mivel csak egyikükkel eshet egybe). Ha mondjuk metszi tj-t - természetesen a C pontban -, akkor a ki és kj körvonalakra illeszkedő gömb középpontja csak C lehet, sugara pedig nem más, mint C és kj távolsága, azaz R. A ki körvonal tehát illeszkedik a C középpontú, R sugarú gömbre.