A 2000. áprilisi számban kitűzött fizika elméleti feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaLban folyamatosan közöljük.

P. 3334. Tibor egy bizonyos útvonalon állandó sebességgel szokott kerékpározni. Egy alkalommal ennek az útvonalnak első x százalékát szokásos sebességénél éppen x százalékkal kisebb sebességgel tette meg. Az útvonal hátralevő szakaszán szokásos sebességének kétszeresével haladt, és így éppen a szokott időben ért célba. A teljes útnak hány százalékát tette meg a szokásosnál kisebb sebességgel? (3 pont)

Takács Gábor, Budapest

Megoldásvázlat. Legyen s az út teljes hossza, v pedig Tibor szokásos sebessége! A teljes út megtételéhez szükséges idő

Innen

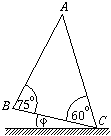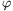P. 3335. Az ábrán látható ABC háromszög A csúcsából az AB és az AC oldalakon súrlódás nélkül csúszhatnak le pontszerű testek. Mekkora legyen az ábrán látható szög, hogy az A pontból kezdősebesség nélkül, egyszerre elengedett testek egyszerre érkezzenek a B, illetve C pontokba? (4 pont)

Varga István, Békéscsaba

Megoldásvázlat. Az és Az szakaszok vízszintessel bezárt szöge rendre 60^o+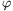 és 75^o-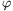, ezért a rajtuk való végigcsúszás idejének a négyzete

illetve

A kettőt egyenlővé téve és kihasználva, hogy

a

egyenletre jutunk, melynek a megoldása 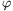=15^o.

P. 3336. A dízel-motorban a gázt adiabatikusan összenyomják. Ha a kezdeti hőmérséklet 27 ^oC, az összenyomás utáni hőmérséklet 681 ^oC lesz. Tegyük fel, hogy a gáz kétatomos molekulákból álló ideális gáznak tekinthető. Mekkora a kezdeti és az összenyomás utáni térfogat aránya (a sűrítési viszony, más néven kompresszió)? (4 pont)

Radnóti Katalin, Budapest

Megoldásvázlat. Egy adott gáz adiabatikus változásakor

ahol =c_p/c_v, kétatomos gáz esetén =7/5. Ennek megfelelően a sűrítés

Megjegyzés. Az üzemanyagkeveréket kétatomos gáznak tekinteni (meglepő módon) nem rossz közelítés. A nagy szénhidrogén molekulák java része apró folyadékcseppek formájában van jelen, de az elpárolgott rész sem befolyásolhatja nagyon a gázmolekulák szabadsági fokainak átlagos számát. Például egy n szénatomból álló szénhidrogén-lánc (C_nH_2n+2) elégetéséhez (3n+1)/2 O₂ molekula kell, ennyi O₂ molekula mellett a levegőben van még négyszer annyi, azaz 2(3n+2) N₂ molekula is, tehát a tökéletes égéshez szükséges keverékben 5(3n+1)/2 kétatomos molekula esik egy nagyobb szabadsági fokú molekulára. n=10 esetén a kétatomos molekulák és a nagyobbak aránya kb. 75:1.)

P. 3337.Egy vízszintes felületen nyugvó, gömb alakúnak tekintett higanycsepp energiája az alábbi formulával adható meg: E=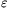V+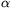A+mgr (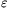>0 állandó, 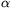a higany felületi feszültsége, r a csepp sugara, A a felszíne, V a térfogata, m pedig a tömege). Mekkora sugarú higanycseppnek van a legkisebb fajlagos (tömegegységre jutó) energiája? Határozzuk meg a sugarat numerikusan is! (4 pont)

Kiss Miklós, Gyöngyös

Megoldásvázlat. Az E fenti kifejezését az

alakba írjuk, ahol a higany sűrűsége. Eszerint a fajlagos energia

Itt az első tag adott, a második és harmadik tag szorzata (így a mértani közepe) pedig állandó. A számtani közép nem lehet kisebb a mértaninál, legfeljebb egyenlő vele akkor, ha a két tag egyenlő. Ebből következik, hogy a a fajlagos energia kifejezésében a második és harmadik tag összege (így a számtani közepe) akkor a legkisebb, ha a két tag egyenlő, azaz

Megjegyzés: A higany (levegőre vonatkoztatott) felületi feszültsége 0,49 J/m². Egyes táblázatok (pl. a Négyjegyű... bizonyos kiadásai) ettől lényegesen különböző (egy nagyságrenddel kisebb) adatokat tartalmaznak. Ez természetesen nem a diákok hibája, a numerikus eredmény ebből adódó hibájáért nem veszítenek pontot.

P. 3338. Az ábrán látható, egyik végén beforrasztott, A keresztmetszetű cső függőleges síkban helyezkedik el. A cső vízszintes részében levő L hosszúságú higanyoszlop L hosszúságú oxigéngázt zár el. A külső légnyomás L magasságú higanyoszlop hidrosztatikai nyomásával azonos.

A cső környezetében a hőmérséklet lassan emelkedik. Mekkora a gáz térfogata akkor, amikor a gáz által végzett munka a felvett hő 20 %-a? (A függőleges szár elegendően hosszú.) (5 pont)

Kotek László, Pécs

Megoldásvázlat. Legyen a higanyoszlop felső vége h magasságban, és jelölje a higany fajsúlyát! A bezárt oxigén térfogata (L+h)A, nyomása pedig (L+h), egészen addig, amíg h<L. A melegítés első szakaszában tehát

(L+h)²A=nRT.

A kezdeti hőmérsékletet T₀-lal jelölve (T₀=L²A/nR) a fenti egyenlet szerint 4T₀-nál h=L, efölött az oxigén állandó 2L nyomás mellett tágul tovább, azaz

(L+h)2LA=nRT.

A melegítés első szakaszában a belső energia változás E_b a hőmérséklet (T) függvényében

míg a tágulási munka L_t, lévén a p-V diagram egy az origón átmenő egyenes (p=V/A),

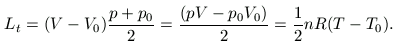
Ezen a szakaszon sehol sem teljesül, hogy a felvett hő Q(=E_b+L_t) és a tágulási munka aránya 5:1 lenne. A második szakaszon a (melegítés kezdetétől mért) E_b-t továbbra is a fenti képlet adja meg, de a (tágulás kezdetétől számított) tágulási munka most

Azt a hőmérsékletet, ahol Q:L_t=5:1 T₁-gyel jelölve fennáll, hogy

Innen T₁=5T₀. Az erre a szakaszra érvényes állapotegyenlet szerint ekkor h=3L/2, azaz az oxigénoszlop teljes hossza 5L/2.

P. 3339.Két R sugarú fémgömböt helyezünk el egymástól r távolságra (r>>R). Az egyiknek Q₁, a másiknak Q₂ töltése van. Legfeljebb mennyi energia fordítódik annak a huzalnak a melegítésére, amellyel a két fémgömböt összekötjük?

Adatok: Q₁=3^.10^-8 C, Q₂=2^.10^-9 C, r=2 m, R=2 cm. (5 pont)

Légrádi Imre, Sopron

Megoldásvázlat. Ahhoz, hogy a két gömböt egymástól igen távol Q₁ ill. Q₂ töltésre töltsük fel

energia kell. Ha ezután a két gömb középpontját egymáshoz r távolságra hozzuk, jó közelítéssel

munkát kell végeznünk.

Megjegyzés. A fenti kifejezés akkor lenne pontos, ha mindkét gömb felszínén egyenletes maradna a töltéssűrűség, de nem marad az, mert az egyik gömb tere megváltoztatja a másik felületi töltéseloszlását és viszont. A fenti közelítés hibáját azonban könyen megbecsülhetjük. Ennek során feltesszük, hogy a Q₁ és Q₂ előjele azonos, de a becslés teljesen analóg akkor is, ha különbözők az előjelek. A kölcsönhatási energia pontos értékét E₁₂-vel jelölve

A két szélső korlátot azok a helyzetek adják, melyekben a töltések a lehető legtávolabb, illetve legközelebb vannak egymáshoz. Felhasználva az

közelítő összefüggést (r>>R),

azaz a két gömb kölcsönhatási energiáját a fenti kifejezés R/r nagyságrendű relatív hibával adja meg. Mivel a kölcsönhatás energiája maga is (R/r)-szer kisebb, mint a gömbök sajátenergiája, ezt a hibát már elhanyagolhatjuk. A töltés-rendszer energiája tehát

A két gömb összekötésekor a töltések kiegyenlítődnek, azaz mindkét gömbön (Q₁+Q₂)/2 töltés lesz. Ekkor az energia értéke

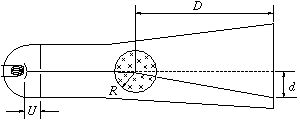
A két energia közötti különbség részben a huzalt melegíti, részben mint egy antennán szétsugárzik. (Elegendően nagy feszültségkülönbség esetén a gömbök fémes összekötésekor szikrázást figyelhetünk meg, ez is tanusítja, hogy elektromágneses sugárzás formájában is távozik energia a rendszerből. Minél nagyobb a huzal ellenállása, annál kevesebb energia sugárzik szét.) A disszipált hő maximális értéke a két energia különbsége, ami némi átrendezés után

P. 3340. Katódsugárcsőben egy tekercs segítségével R=2 cm sugarú, kör keresztmetszetű, homogén mágneses mezőt hoztunk létre. Amikor a tekercset bekapcsoljuk, az U=250 V feszültséggel felgyorsított elektronnyaláb eltérése a tekercs tengelyétől D=20 cm távolságban levő ernyőn d=10 cm. Mekkora az eltérítő mágneses mező indukciója? (A tekercs bekapcsolása előtt a nyaláb áthaladt a tekercs tengelyén.) (4 pont)

Holics László, Budapest

Megoldásvázlat. Az elektronsugár (elektronnyaláb) a mágneses térben körpályán halad. A pálya köríve mindkétszer merőlegesen metszi a tér határát jelentő kört, ezért a kilépő nyaláb (visszafelé történő) meghosszabbítása ugyanúgy átmegy a tekercs tengelyén, ahogy a belépő nyalábé. Igy a nyaláb 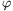=arctg(d/D) szöggel térül el. A geometriából következik, hogy a pálya körív szakaszához tartozó központi szög ugyancsak 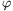, igy a a pályaív sugara r=R/tg(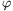/2). A pálya görbületét a Lorentz-erő okozza, ezért

másrészt a sebesség és a gyorsítófeszültség között fennáll, hogy

(ahol m és e az elektron tömege és töltése). E két összefüggésből

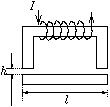P. 3341. Egy elektromágnes U alakú vasmagjának keresztmetszete A, középvonalának hossza L. A záró vasmag l hosszú és szintén A keresztmetszetű. Amikor a záró vasmag h távolságra van az U alakú vasmagtól, amelyen lévő tekercsben I áram folyik, a záró vasmagot F erővel húzza magához az elektromágnes. A vas permeabilitása nem állandó, de a mágneses indukciótól való 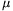(B) függését ismerjük.)

a) Hány menetből áll a tekercs?

b) Mekkora erővel szorítja magához az elektromágnes a záró vasmagot, ha nincs közöttük légrés? Mekkora ekkor a mágneses indukció és a relatív permeabilitás értéke a vasban?

Adatok: L=30 cm, l=12 cm, A=10 cm², h=1 mm, I=1 A, F=500 N, és 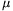(B)=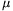₀(4500-2500 T^-1 B) a vizsgált tartományban. (5 pont)

Radnai Gyula, Budapest

Megoldásvázlat. a) Először tekintsük a légréses esetet! Az elektromágnes emelőereje (mivel mindkét végének a felülete A)

ahonnan

Másrészt a jelen elrendezésben (a két légrés együttes szélessége 2h, a zárt kör középvonalának a vasmagban futó része (L+l) hosszú) a mágnesben fellépő mágneses indukció

Ebből n=1370 adódik.

b) Ha nincs légrés, a

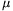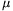egyenletet B-re megoldva B=1,64 T adódik. B ezen érteke mellett (B)= 400₀5^.10^-4 T. Most a mágnes emelőereje

P. 3342. Az ²³⁸U atommag gyors neutron lövedék hatására bekövetkező hasadásakor a következő magreakció jöhet létre:

.

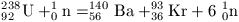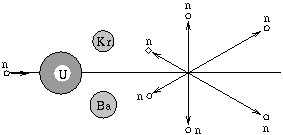
Tételezzük fel, hogy a hasadási folyamat az ábrán látható módon játszódik le, és fennállnak az alábbiak:

a) a beérkező gyors neutron mozgási energiája 3,2^.10^-13 J;

b) a keletkező 6 neutron egy síkban, a beérkező neutron mozgásirányára szimmetrikusan, egymással 60^o-60^o-os szöget bezárva repül szét;

c) a felszabaduló magenergia 2,88^.10^-11 J;

d) a merőlegesen szétrepülő és a ,,hátrafelé'' repülő neutronok mozgási energiája azonos: 1,6^.10^-13 J;

e) a keletkező Kr és Ba hasadvány magok is merőlegesen repülnek szét.

Mekkora külön-külön a hasadványok mozgási energiája? (5 pont)

Tolna megyei Szilárd Leó fizikaverseny

Megoldásvázlat. Jelölje E₀ a bejövő neutron energiáját, m a tömegét és a lendületét! Az energiát számolhatjuk E₀ egységekben: a merőlegesen és ferdén hátra repülő neutronok energiája E₀/2 (ennek megfelelően az impulzusuk p₀/), a hasadáskor felszabaduló energia pedig 90E₀. A Kr és a Ba magok tömege m_Kr=93m ill. m_Ba=140m. A ferdén előre repülő neutronok lendületét az impulzusmegmaradás adja meg:

.

így ezen neutronok energiája

.

Az energia-mérleg szerint a Kr és a Ba mag együttes mozgási energiája

E_Kr+Ba=E_Kr+E_Ba=85,7E₀,

az impulzusmegmaradás szerint pedig az impulzusuk nagysága azonos:

.

Ezeket az egyenleteket megoldva

.

Végül E₀ értékét behelyettesítve E=5,3^.10^-13 J, E_Kr=1,64^.10^-11 J, E_Ba=1,1^.10^-11 J.

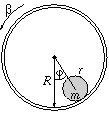P. 3343. Egy R belső sugarú, rögzített tengelyű csövet kicsiny 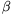szöggyorsulással kezdünk mozgatni.

A cső belsejébe egy tömör, homogén anyageloszlású, m tömegű, r sugarú rudat helyeztünk. (A súrlódás olyan nagy, hogy a rúd mindvégig tisztán gördül a csőben.)

a) Mekkora legyen az ábrán látható 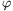szög, hogy a rúd tengelye helyben maradjon?

b) Hogyan mozog a rúd, ha induláskor a cső alján állt? (6 pont)

Balogh Péter, Budapest

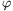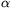Megoldásvázlat. Miközben a külső cső forog, a belső rúd benne a paláston gurul, és közben persze a tengelyének helyzetét megadó szög is változhat. Jelölje a rúd tengelyének a cső tengelye körüli forgásának szöggyorsulását , a 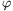szög változási (szög)sebességét , (szög)gyorsulását pedig . (Legyen mindegyik mennyiség akkor pozitív, ha az óramutató járásával ellentétes irányú.) Csúszásmentes gördülés esetén a két henger éppen érintkező alkotóinak a gyorsulása azonos:

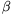R=(R-r)+r.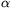

A belső henger tengelyének érintő irányú gyorsulását az

m(R-r)=S-mgsin,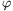

míg a tengely körüli forgás gyorsulását a

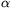mr²=Sr

egyenlet adja meg. (Itt S a súrlódási erő, amely nyiván érintőleges.) S és 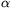kiküszöbölése után

.

a) Ha sin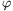(t=0)=(R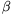/2g) és (t=0)=0, akkor a belső henger, bár gyorsulva forog, a tengely helyzete mozdulatlan marad.

b) Más kezdeti feltételeknél a belső henger a fenti ,,egyensúlyi'' helyzet körül rezeg. Kihasználva, hogy kis szögekre sin,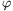

.

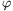ahonnan

.

A 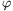(t=0)=(t=0)=0 kezdeti feltételnek az

felel meg, azaz