A 2000 májusi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 239. Szerkesszük meg a háromszöget, ha adott az a három pont, ahol a súlyvonalak meghosszabbításai metszik a körülírt kört.

Javasolta: Rácz János, Budapest

Megoldásvázlat. A megoldás során többször felhasználjuk, hogy ha egy másodfokú egyenlet együtthatóit ismerjük, akkor az egyenlet gyökeit is meg tudjuk szerkeszteni.

Legyenek a háromszög csúcsai A, B, C, a súlypont S, a súlyvonalak meghosszabbításainak metszéspontjai a körülírt körrel A₁, B₁, C₁. Legyen az ABC háromszög oldalainak és súlyvonalainak, valamint az A₁B₁C₁ háromszög oldalainak hossza a, b, c; s_a, s_b, s_c illetve a₁, b₁, c₁.

Legyen h az S pontnak a körülírt körre vonatkozó hatványa. Ekkor SA^.SA₁=SB^.SB₁=SC^.SC₁=|h|. A kerületi szögek tétele miatt a BCS és C₁B₁S háromszögek hasonlóak, ezért

Ebből láthatjuk, hogy a₁:b₁:c₁=as_a:bs_b:cs_c.

Legyen , , és . Az a₁, b₁, c₁ szakaszok ismeretében p és q könnyen megszerkeszthető.

Ismeretes, hogy , és . Az előbbi egyenletekbe behelyettesítve ezeket, az x, y számokra a következő egyenletrendszert kapjuk:

x(2+2y-x)=p(2x+2y-1);

y(2+2x-y)=q(2x+2y-1).

Az első egyenletből . Ezt beírva a második egyenletbe, majd -tel szorozva

Ez -re egy másodfokú egyenlet, ezért ezt a számot is meg tudjuk szerkeszteni. Ha már ismerjük -t, akkor x-et egy újabb másodfokú egyenlet gyökeként szerkeszthetjük meg.

Az x után y-t is megszerkeszthetjük, ezzel már ismerjük az a, b, c oldalak arányát.

A. 240. Legyenek n és m pozitív egészek. Bizonyítsuk be,

( az Euler-féle függvény.)

Megoldásvázlat. Legyenek m prímosztói p₁, ..., p_s. Ekkor minden 1 és n közötti egész szám egyértelműen előállítható alakban, ahol 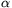₁, ..., 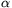_s nemnegatív egészek, k pedig olyan 1 és n közötti egész, ami relatív prím m-hez. Más szóval, ha a

szorzatban elvégezzük a beszorzást, akkor az 1, 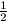, ..., számok mindegyikét pontosan egyszer megkapjuk (valamint további tagokat is). Ezért

A. 241. Igazoljuk, hogy tetszőleges n pozitív egész esetén

Megoldásvázlat.

A megoldás során az k binomiális együtthatókat valós x-ekre is kiterjesztjük a következőképpen:

Felhasználjuk még, hogy tetszőleges k,l nemnegatív egészekre

azt, hogy tetszőleges k nemnegatív egészre

valamint azt az ismert tételt, hogy teszőleges x,y valós számokra és n nemnegatív egészre

(1)  

(Utóbbi részletes bizonyítását lásd pl. R. L. Graham -- D. E. Knuth -- O. Patashnik: Konkrét matematika, 169. oldal. Rögzített n esetén (1) két oldala egy-egy polinom. Ha ezek értéke tetszőleges pozitív egész x,y esetén megegyezik, akkor a két polinom azonos. Pozitív egész x,y esetén viszont a bizonyítás egyszerű kombinatorikus okoskodással elvégezhető.)

A felsorolt tételek alapján, tetszőleges 0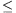m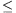n egészek esetén

(2)  

Az (2) azonosságból n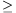2-re azonnal következik a feladat állítása (n=1-re behelyettesítéssel ellenőrizzük):

Harangi Viktor dolgozata alapján