A 2000. májusi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 585. Bizonyos magnókazettákban 0,0075 mm vastagságú szalag tekeredik a 11 mm átmérőjű orsókra. Az orsók középpontjainak távolsága 42 mm. Legfeljebb hány méter szalag lehet egy használható magnókazettában? (A tele orsóról a szalagnak akadálytalanul át kell jutnia az üres orsóra.)

Megoldásvázlat. Ha egy bizonyos helyzetben a két tekercs sugarait R₁ és R₂ jelöli, akkor (mm-ekben számolva) R₁+R₂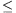42 kell legyen. Ekkor (felülről nézve) az orsókra csévélt magnószalag összterülete t=(R₁²+R₂²)-2r², ahol r=5,5 az egyes orsók sugara. Másrészt t=l^.d, ahol l a szalag hossza, d=0,0075 pedig annak vastagsága. Ha R₁²+R₂² rögzített, akkor R₁+R₂ pontosan akkor a lehető legnagyobb, ha (R₁+R₂)², vagyis a lehető legnagyobb. A számtani és mértani közepek közötti egyenlőtlenség alapján (az egyenlőség esetének diszkusszióját is figyelembe véve) ez pedig akkor következik be, ha R₁=R₂. Vagyis a lehető leghosszabb magnószalagot feltételezve, a két tekercs pontosan a műsoridő felénél fog érintkezni, amikor R₁=R₂=21. A szalag hossza ebben az esetben (mm-ben) , vagyis körülbelül 344,1 méter.

C. 586. Legfeljebb hány oldalú az a konvex sokszög, amelynek nincs két szomszédos tompaszöge?

Megoldásvázlat. Ha a sokszögnek n oldala van, akkor szögeinek összege (n-2)180^o. Ha ebből k nem tompaszög, akkor (n-2)180^o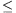(n-k)180^o+k^.90^o. Innen k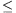4 és egyenlőség csak k=n esetén lehet. Így vagy k=n=4 vagy k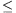3. Ha nincs két szomszédos tompaszög, n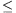2k kell legyen, így n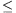6. Hat oldala lehet is egy ilyen sokszögnek, például ha egy szabályos hatszög minden oldalára egy fél szabályos háromszöget illesztünk az ábrán látható módon (ennek a hatszögnek három derékszöge és három 150^o-os szöge lesz):

C. 587. Legyen n pozitív egész. Az x-tengely n abszcisszájú pontját összekötjük az y-tengely n-1 és n+1 ordinátájú pontjaival, továbbá az y-tengely n ordinátájú pontját összekötjük az x-tengely n-1, illetve n+1 abszcisszájú pontjaival. Mekkora területű négyszöget zár közre ez a négy szakasz?

Megoldásvázlat. Legyenek az ábra szerint A(0,n-1), B(0,n), C(0,n+1), D(n-1,0), E(n,0), F(n+1,0).

T=T(EPBQ)=T(AEC)-T(AQB)-T(BPXC). Itt T(AEC)=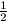^.2^.n, T(AQB)=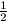y_q és T(BPC)=, ahol (x_p,y_p) és (x_q,y_q) a P és Q pont koordinátái. Szimmetria okokból x_p=y_p és x_q=y_q. A CE egyenesének egyenlete nx+(n+1)y=n(n+1), innen . A BD egyenesének egyenlete (n-1)x+ny=(n-1)n, innen , .

C. 588. Írjuk fel az f:(-, -2)R, x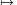2x²+8x+7 függvény inverzét.

Megoldásvázlat. Ha y=2x²+8x+7=2(x+2)²-1, akkor (x+2)²=(y+1)/2. Minden x<-2 értékhez egy y>-1 érték tartozik, és minden y>-1 esetén (y+1)/2 >0 és létezik pontosan egy z<0 szám, melyre z²=(y+1)/2, vagyis pontosan egy x<-2 szám, melyre (x+2)²=(y+1)/2. A függvény inverze tehát a g:(-1,)R

függvény.

C. 589. Egy V keresztmetszetű vízlevezető árokban elakadt egy egyenes bot. A bot két vége az árok két különböző oldalához ér hozzá, és a két oldal síkjával azonos nagyságú szöget zár be. Mutassuk meg, hogy ekkor a bot két vége egyenlő távolságra van az árok aljától.

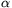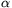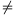Megoldásvázlat. Jelölje az árok két oldalának síkját S₁ és S₂. A botnak S_i-n levő végét jelölje P_i, mely az árok aljától m_i távolságra van (i=1,2). Tegyük fel, hogy a bot az S₁, S₂ síkokkal szöget zár be, az S₁ és S₂ síkok szöge pedig . Ekkor P₁ távolsága az S₂ síktól m₁sin, így P₂ távolsága az S₁ síktól m₂sin. Másrészt mindkét távolság lsin-val egyenlő, ahol l a bot hossza. Mivel sin0, ebből m₁=m₂ következik.