A 2000. szeptemberi számban kitűzött fizika elméleti feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3353. Egy locsolóautó tartályában 16 m³ víz van, amelynek hatására a tartályt tartó rugószerkezet 8 cm-t nyomódik össze. Az autó 10 perc alatt 250 métert tesz meg egyenletesen haladva, miközben másodpercenként 16 liter vizet locsol az útra. Ekkor elered az eső, az autó beszünteti a locsolást, és egyenletes mozgással visszatér kiindulási helyére, miközben 3,0 kN nagyságú tolóerő hat rá.

a) Hány cm a rugó összenyomódása, miközben az autó visszatér kiindulási helyére?

b) Legalább mennyi munkát végez az autó motorja az oda-vissza úton, ha a vontatáshoz szükséges erő az összsúly 2,5 %-a? (4 pont)

Jedlik Ányos Országos Fizikaverseny (6-7. osztály), Nyíregyháza

Megoldás. a) Tíz perc alatt 600 s^.16^.10^-3m³/s=9,6 m³ víz folyik ki a tartályból. Ez után a rugó összenyomódása 8 cm^.(16-9,6)/16=3,2 cm.

b) A visszafele úton végzett munka 250 m^.30^.10³ N=7,5^.10⁶ J. Az oda úton az erő átlaga 30^.10³+0,5^.0,25^.9,6 m^3.10⁴ N/m³=42^.10³ J, azaz az ekkor végzett munka 250 m^.42^.10³ J=10,5^.10⁶ J. Az összes munka tehát 1,8^.10⁷ J.

P. 3354. Az 1300 cm³-es SUZUKI SWIFT személygépkocsi 5,4 liter benzint fogyaszt 100 km-en, 90 km/h állandó sebesség mellett. Amikor a gépkocsi 160 km/h csúcssebességgel megy, akkor a motor által leadott teljesítmény 48,3 kW. A motor hatásfoka 30 %, a benzin sűrűsége 700 kg/m³, égéshője 46 000 kJ/kg.

a) Hány liter benzint fogyaszt ekkor 100 km-en?

b) Mekkora a leadott teljesítmény 90 km/h sebességnél? (3 pont)

Öveges József emlékverseny (9-10. osztály), Tata

Megoldás. Legyen a motor leadott teljesítménye egy adott v sebességnél W_v, a fogyasztása literben V_v, a hatásfoka , s=10⁵ m és Q az üzemanyag egy literre vonatkoztatott égéshője (adatainkkal Q=46^.10^6.700^.10^-3 J/l=32,2 MJ/l). Az energiamegmaradás szerint

V_vQ=W_vs/v. Ebből az összefüggésből a) V₁₆₀=11,25 l és b) W₉₀=13,04 kW.

P. 3355. Egy teniszversenyen a második helyezett ezüstből készült érmet kap. Az érmet úgy készítették, hogy a kezdetben 20 ^oC-os anyagot megolvasztották, és formába öntötték. Mennyi idő alatt olvadt fel 20 darab 5 dkg-os éremhez szükséges ezüst, ha az olvasztókemencét 230 V-os hálózatról üzemeltették, a kemence fűtőszálának ellenállása 46 , a hatásfok 40 %? (Az ezüst olvadáspontja 960 ^oC, fajhője 0,2 kJ/(kg ^oC), olvadáshője 100 kJ/kg.) (3 pont)

"Keresd a megoldást!" verseny, Szeged

Megoldás. A kemence által az ezüstnek átadott hő az ezüstöt előbb az olvadáspontra melegíti, majd megolvasztja, azaz

(Itt U a feszültség, R a fűtőszál ellenállása, a hatásfok m az ezüst teljes tömege, c a fajhője, L az olvadáshő, T a kezdő és az olvadási hőmérséklet különbsége, végül t a keresett időtartam.) Innen t=626 s.

P. 3356. Legfeljebb hány fokos lejtőn állhat meg egy homogén, tömör félgömb a domború oldalán? Mekkora súrlódási együttható kell ehhez? (A félgömb tömegközéppontja a sugár 3/8-ában van.) (4 pont)

Lánczos Kornél verseny, Székesfehérvár

Megoldás. A nyugvó félgömb mindig úgy áll, hogy a súlypontja az alátámasztási pont fölött van, míg a középpont a lejtőt az alátámasztási pontban döfő, arra merőleges egyenesre esik. Az általános esetben tehát a középpont köré az eredeti sugár 3/8-ával húzott gömböt az alátámasztási ponton átmenő függőleges döfi, de a határesetben csak érinti. Ebből a geometriából a határesetben a lejtő szögére sin =3/8 adódik, azaz =22^o. A súrlódási együtthatóra fennáll, hogy 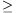tg =0,4.

P. 3357. Tapasztalatból tudjuk, hogy ha egy nyitott szájával lefelé tartott szemeteszsákot megtöltünk meleg levegővel, akkor a zsák - a hőlégballonhoz hasonlóan - felemelkedik.

Hol a hiba a következő gondolatmenetben: "A zsák szája nyitott, ezért a külső és a belső levegő nyomása egyenlő. A zsák (felül levő) zárt alját ezért a belső levegő ugyanakkora erővel nyomja felfelé, mint a külső levegő lefelé. Ezek az erők kiegyenlítik egymást, tehát a zsák anyagára ható nehézségi erő miatt a zsák leesik." (4 pont)

Országos Középiskolai Tanulmányi Verseny

Megoldás. A zsák szájánál ugyan azonos a külső és a belső nyomás, de a magasság függvényében másképp változik kint és bent: kint gyorsabban csökken. Ez vezet a zsákot felemeló nyomáskülönbséghez.

Részletesebb számítás: Legyen a nyomás a magasság függvényében p(h)! Erre igaz, hogy kicsiny h esetén

p=-(h)gh, ahol p=p(h+h)-p(h),

és (h) a gáz sűrűsége a h magasságban. Ugyanakkor az univerzális gáztörvény szerint

p(h)=r(h)T(h) (itt r az univerzális gázállandó osztva a gáz moláris tömegével, T(h) pedig a hőmérséklet). Ennek alapján

, azaz .

A külső, illetve belső viszonyokra k illetve b indexekkel utalva tehát

.

Abból tehát, hogy a zsák szája h₀ magasságában p_k(h₀)=p_b(h₀), és hogy afölött T_b(h)>T_k(h) már következik, hogy

p_b(h)>p_k(h),

sőt az is, hogy p_b(h)-p_k(h) a magassággal monoton nő!

P. 3358. Megtervezendő egy útkanyar a következő feltételekkel: amikor az út jeges (0,08 a tapadási súrlódási együttható), az álló autó nem csúszhat a kanyar közepe felé, ezen kívül 60 km/h-nál kisebb sebességeknél nem sodródhat kifelé. Mekkora lehet a legkisebb pályasugár? A vízszinteshez képest mekkora szögben kell megdönteni az úttestet a legkisebb sugárnál? (4 pont)

Budó Ágoston verseny, Szeged

Megoldás. Legyen a megadott súrlódási együttható , a pályasugár r, az út dőlésszöge , és a maximális sebesség v! Ha az álló kocsi nem csúszik be,

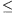
₀, ahol tg ₀=. Ha v sebesség mellett a kocsi nem csúszik ki,

,

azaz

Ha a sugár elég nagy, a kocsi biztos nem csúszik ki (a bal oldal negatív). A sugár csökkentésével a bal oldal jobban nő, és a legkisebb pályasugárnál pont az egyenlőség teljesül. Innen

.

Eszerint r akkor a legkisebb, ha a legnagyobb, tehát =₀. Adatainkkal =4,57^o, r=172,5 m.

P. 3359. Két megegyező méretű, fehérre festett acél- és rézhengert ugyanarra a hőfokra felmelegítünk, majd kitesszük hűlni azokat az asztalra (nem közvetlenül egymás mellé). Azt tapasztaljuk, hogy a rézhenger hamarabb hűl ki. Mi lehet a magyarázat? (A réz és az acél fajhője és a sűrűsége is közel ugyanakkora.) (5 pont)

Öveges József Országos Fizikaverseny (8. osztály), Tata

Megoldás. Az egyszerűsítő feltevés szerint a két azonos méretű és kezdeti hőmérsékletű hengerben tárolt hőmennyiség azonos. A hengerek fehér színe (és a feltehetően nem túlságosan magas hőmérséklete) miatt a hőleadás elsősorban közvetlen hőátadással történik (a sugárzás szerepe elhanyagolható), ennek mértéke a felület és a környezet közötti hőmérsékletkülönbséggel arányos. Mivel a réz hővezetési együtthatója lényegesen (a vörösrézé mintegy hatszor-hétszer, de a sárgarézé is kétszer) nagyobb mint az acélé, a hűlés során a réz hőmérsékleteloszlása egyenletesebb mint az acélé, így azonos "hőtartalom" mellett nagyobb a felületi hőmérséklete, tehát gyorsabb a hőleadása.

P. 3360. Legalább milyen magasról esett az üveglapra egy 1 mm átmérőjű, gömb alakú higanycsepp, ha 1000 darab egyforma gömbbé esett szét? (4 pont)

Bay Zoltán verseny, Sarkad

Megoldás. A kezdeti (helyzeti + felületi) energia

.

Itt h a középpont magassága, r=5^.10^-4 m a csepp sugara, =13 500 kg/m³ a higany sűrűség és =0,5 N/m a felületi feszültség. Az energia a leesés után

.

A higany (helyzeti + felületi) energiája nem nőhet (sőt, ténylegesen csökken, hiszen az ütközés disszipatív folyamat, melynek során hő is fejlődik), így

.

P. 3361. Egy soros gerjesztésű, egyenáramú motort 100 V feszültségre kapcsolunk. Indulás előtt a motor 16 A áramot vesz fel, majd forogni kezd. Mire a fordulatszáma állandóvá válik, a motoron átfolyó áram 4 A-re csökken. A motort dinamónak akarjuk használni, és ugyanakkora fordulatszámon üzemeltetjük, mint amikor motor volt. Mekkora terhelő ellenállást kell a dinamóra kötni, ha azt akarjuk, hogy a dinamón is 4 A áram folyjon át, és mekkora ebben az esetben a dinamónak a terhelő ellenálláson leadott teljesítménye? (4 pont)

Bicentenáriumi Jedlik Ányos verseny, Győr

Megoldás. Az álló motorra kapcsolt U feszültség által hajtott I₀ áramot a motor R_b ohmikus belső ellenállása határozza meg:

I₀=U/R_b.

Egy adott fordulatszámon forgó soros gerjesztésű motor tekercseiben egy elektromotoros erő indukálódik úgy, hogy

U=IR_b+.

Ugyanezen fordulatszám mellett a dinamónak használt motor elekromotoros ereje is , tehát

=I(R_b+R),

ahol R a külső terhelő ellenállás. Ezekből az egyenletekből R=12,5, és a rajta disszipálódó teljesítmény P=I²R=200 W.

P. 3362. A mérések azt mutatják, hogy egy elhanyagolható sebességű atommag bomlása során 5,5 MeV mozgási energiájú -részecskét sugároz ki.

a) Mekkora az -részecske sebessége, illetve a bomlás során keletkezett mag visszalökődési sebessége?

b) Mekkora energia szabadul fel egy mag bomlása során?

c) Mekkora energia szabadul fel 1 mg tiszta radonból 3,82 nap alatt, ha a 222-es radonizotóp felezési ideje éppen 3,82 nap? (4 pont)

Wigner Jenő verseny, Békéscsaba

Megoldás. a) Az rész sebességét az E=mv²/2 nemrelativisztikus képlettel számolva v=1,62^.10⁷ m/s adódik. (Ez rögtön igazolja is a képlet használatának jogosságát: a relatív hiba (v/c)²0,003 nagyságrendű.) A magok visszalökődési sebességét a lendület megmaradásából számolva v_Po=(m/m_Po)v=3,0^.10⁵ m/s-ot kapunk.

b) A sebességek arányát felhasználva a magok energiájára E_Po=(m/m_Po)E adódik, innen a teljes felszabaduló energia E=E+E_Po=((m_Po+m)/m_Po)E=(m_Rn/m_Po)E, azaz 5,6 MeV.

P. 3363. Legfeljebb hány fokra melegíthető fel napfény segítségével egy kicsiny, gömb alakú fekete test egy olyan vékony lencse felhasználásával, amelynek fókusztávolsága az átmérőjének kétszerese? Függ-e az eredmény a kicsiny gömb sugarától? (5 pont)

Olimpiai válogatóverseny, Budapest

Megoldás. Legyen a Nap felszíni hőmérséklete T_N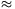6000 K, sugara R és a Nap-Föld távolság D, jelölje továbá a lencse sugarát r, a fókusztávolságát pedig f. A Nap által kisugárzott teljes teljesítmény

4R²T_N⁴, és ebből a lencsére jut r²/4D² hányad, azaz a Nap képét

teljesítmény világítja meg. A Nap képének a sugara

.

így

.

A kép minden pontja azonos fényességű, és a kép egységnyi felületű darabjára

.

teljesítmény érkezik. Egy ezzel a teljesítménnyel megvilágított tárgy addig a T hőmérsékletig melegszik, amíg a felvett teljesítmény és a test által kisugárzott AT⁴ teljesítmény azonos nem lesz. Mivel ez utóbi függ a test A felületétől, T függ a geometriától. Ha pl. a test egy elhanyagolható vastagságú 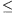s sugarú korong lenne, akkor a felvett teljesítmény w² a leadott pedig 2²T⁴, így T=(1/32)^1/4T_N.

Ha a test egy =s sugarú gömb, a felvett teljesítmény éppen P, a leadott pedig 4s²T⁴, innen T=(1/64)^1/4T_N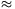2100 K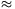1800 C.

Ha a gömb sugara kisebb, mint a Nap képének sugara (<s), akkor is ugyanennyire melegszik fel a gömb. Legyen pl. a gömb sugara 2-szer kisebb, mint a képé. Ekkor az időegységenként rá eső sugárzás energiája 1\over 4-e, de mivel a gömb felszíne is negyede az s sugarú gömbének, ugyanakkora hőmérsékleten 4-szer kevesebb energiát sugároz ki.

Amennyiben a gömb sugara nagyobb, mint a Nap képének sugara, továbbá az anyaga elég jó hővezető, akkor a hőmérséklete kisebb lesz, mint a fentebb számított érték, hiszen a napfényből kapott energiát nagyobb felületen sugározza ki, mint a korábban számított esetben.