A 2000. októberi B-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
B. 3392. Adott 25 edény, űrtartalmuk rendre 1,2,...,25 liter. Hányféleképpen választható ki közülük tíz úgy, hogy bármely két kiválasztott edény felhasználásával kimérhető legyen 1 liter víz? (Korlátlan mennyiségű víz áll rendelkezésre, és egyik edényből a másikba is lehet töltögetni.) (4 pont)
Javasolta: Kozma László, Székelyudvarhely
Megoldás. Egy a és egy b literes edénnyel akkor mérhető ki 1 liter, ha a és b relatív prímek, azaz a-nak és b-nek nincs közös prímosztója. Az 1, 2, ..., 25 számok között kilenc prím van: 2, 3, 5, 7, 11, 13, 17, 19 és 23; bármelyik prímnek legfeljebb egy többszöröse lehet a tíz edény között. Ebből máris következik, hogy az 1 literes edényt mindenképpen ki kell választani, a többi edény űrtartalmaz pedig csupán egyetlen prímszámmal lehet osztható. Az ilyen tulajdonságú edények a prímhatványok.
Mindenképpen ki kell tehát választani:
Ez összesen 4.2.2=16 lehetőség.
B. 3393. Mekkora az ABC háromszög és az A'B'C' háromszög területének aránya, ha az AA', BB', CC' szakaszok felezőpontjai rendre B', C', A'? (3 pont)
Megoldás. A területek aránya 7:1.

B. 3394. Bizonyítsuk be, hogy pontosan akkor szerkeszthető a, b és c hosszúságú oldalakkal háromszög, ha az a, b, c pozitív valós számokra teljesül, hogy (a2+b2+c2)2>2(a4+b4+c4). (3 pont)
Megoldás. Az egyenlőtlenség két oldalának különbsége szorzattá alakíthtó:
(a+b+c)(a+b-c)(a+c-b)(b+c-a)>0.
Ez pontosan akkor teljesül, ha a háromszög-egyenlőtlenség mindegyik oldalra fennáll, azaz a<b+c, b<c+a és c<a+b.
B. 3395. Szerkesszük meg az A1A2A3A4A5 ötszöget, ha adott az Ai pontnak az Ai+1 pontra vonatkozó tükörképe (i=1,...,5,A6:=A1). (3 pont)
Megoldás. Jelöljük Bi-vel az Ai-nek Ai+1-re vonatkozó tükörképét. Ha egy tetszőleges O pontból helyvektorokat indítunk a szereplő pontokhox, és mindegyiket a megfelelő kisbetűvel jelöljük, akkor a tükrözés miatt felírhatjuk a következő egyenleteket:
a1+b1=2a2, a2+b2=2b3, a3+b3=2a4, a4+b4=2a5, a5+b5=2a1.
Ebből az egyenletrendszerből az ai vektorokat kifejezhetjük a bi vektorok segítségével (pl. a1=(b1+2b2+4b3+8b4+16b5)/31), s így az ötszög csúcsait megszerkeszthetjük.
A feladatnak mindig egy megoldása van, azonban a kapott ötszög lehet hurkolt, vagy elfajuló is.
B. 3396. Oldjuk meg az xy+yz+zx-xyz=2 egyenletet, ha x, y és z pozitív egész számok. (4 pont)
Megoldás. Keressük meg először azokat a megoldásokat, amelyekben az ismeretlenek közül x az (egyik) legkisebb; ezekből az összes megoldás, az egyenlet szimmetriája miatt, az x, y és z számok permutálásával kapható.
Az egyenletből
0<xy+yz+zx-xyz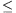 3yz-xyz=(3-x)yz;
3yz-xyz=(3-x)yz;
Ebből következik, hogy 3-x>0, azaz x=1 vagy x=2.
Ha x=1, akkor az egyenlet szerint y+z=2, azaz y=z=1.
Ha x=2, akkor az egyenlet szerint 2y+2z-yz=2. Átrendezve és szorzattá alakítva
(y-2)(z-2)=2.
A két tényező nem lehet (-1)-nél kisebb, ezért csak az 1.2 szorzat lehetséges, azaz y és z értéke valamilyen sorrendben 3 illetve 4.
Az összes számhármas tehát, amire az egyenlet teljesül: (1,1,1) és (2,3,4), beleértve az utóbbi permutációt is.
B. 3397. ABC egy hegyesszögű háromszög, a KLMN pedig egy olyan téglalap, hogy N az AC szakaszra, K és L pedig az AB szakaszra illeszkedik. Toljuk el a KLMN téglalapot az AC-vel párhuzamosan úgy, hogy M' a BC szakaszra kerül. Így kapjuk a K'L'M'N' téglalapot. Mutassuk meg, hogy CL' és AB metszéspontját az AM és CB metszéspontjával összekötő egyenes merőleges az AB egyenesre. (4 pont)
Megoldás. Jelöljük CL' és AB metszéspontját P-vel, AM és CB metszéspontját Q-val. Az eltolás miatt a KK', LL', MM' és NN' szakaszok párhuzamosak és egyenlő hosszúak.

A párhuzamos szelők tétele szerint, AC és LL'
párhuzamosságából  . Hasonlóképpen
AC és MM' párhuzamosságából
. Hasonlóképpen
AC és MM' párhuzamosságából  . A két egyenletet összevetve
. A két egyenletet összevetve  , ebből pedig következik, hogy PQ és
M'L' párhuzamosak, vagyis PQ merőleges AB-re.
, ebből pedig következik, hogy PQ és
M'L' párhuzamosak, vagyis PQ merőleges AB-re.
B. 3398. Az ABCD pontok úgy helyezkednek el a térben, hogy az AB és CD szakaszok hossza 4 egység, míg a BC és DA szakaszok hossza 5 egység. Jelölje az AC és BD szakaszok hosszának négyzetét rendre x és y. Ábrázoljuk a koordináta-rendszerben az így adódó x,y számpárok halmazát. (4 pont)
Javasolta: Hraskó András, Budapest
Megoldás. Legyen E és F az A, illetve C pontok vetülete a BD egyenesre.

Könnyen ellenőrizhető, hogy a pontrendszer létezéséhez szükséges és elegendő
a  feltétel teljesülése. Némi számolással
ellenőrizhető, hogy a baloldali egyenlőtlenség az xy
feltétel teljesülése. Némi számolással
ellenőrizhető, hogy a baloldali egyenlőtlenség az xy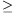 81, a jobboldali az x+y
81, a jobboldali az x+y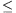 82 egyenlőtlenséggel ekvivalens. A keresett ponthalmaz tehát az
xy=81 hiperbola pozitív ága és a x+y=82 egyenes által
közrezárt, zárt tartomány:
82 egyenlőtlenséggel ekvivalens. A keresett ponthalmaz tehát az
xy=81 hiperbola pozitív ága és a x+y=82 egyenes által
közrezárt, zárt tartomány:

B. 3399. Adott a síkon két kör, e és f, rajtuk kívül pedig a P pont. A P -ből egy-egy érintőt húzunk a két körhöz, ezek érintési pontja E és F. Bizonyítsuk be, hogy azoknak a szakaszoknak az aránya, amelyeket a két kör metsz ki az EF egyenesből, nem függ attól, hogy melyik két érintőt rajzoltuk meg. (5 pont)
Megoldás. Könnyen belátható -- merőleges szárú szögek segítségével
--, hogy ha az EF egyenes által az e illetve f körből
kimetszett húrokhuz tartozó középponti szög 2 illetve 2
illetve 2 , akkor az
EPF háromszögben E-nél illetve F-nél lévő szöge
, akkor az
EPF háromszögben E-nél illetve F-nél lévő szöge  illetve
illetve  . A szinusztétel szerint
. A szinusztétel szerint
sin /sin
/sin =OF/OE.
=OF/OE.
A jobb oldalon álló tört értéke állandó, mert egy külső pontból egy körhöz húzható érintő szakaszok hossza állandó. A bal oldalon lévő tört számlálóját illetve nevezőjét az e illetve az f kör sugarának kétszeresével szorozva viszont éppen a körökből az EF egyenes által kimetszett húrok hosszának hányadosát kapjuk, tehát ez a hányados is állandó.
B. 3400. Adott d egész számra legyen Sd={x 2+dy2:x,y
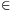 Z}
. Tegyük fel, hogy a
Z}
. Tegyük fel, hogy a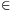 Sd és b
Sd és b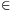 Sd olyanok, hogy b prím és
Sd olyanok, hogy b prím és
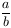 egész. Bizonyítsuk be, hogy ekkor
egész. Bizonyítsuk be, hogy ekkor
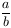
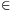 Sd. (5 pont)
Sd. (5 pont)
Javasolta: Csörnyei Marianna, London
Megoldás. Legyenek x, y, u, v olyan egész számok, amelyekre a=x2+dy2 és b=u2+dv2. Könnyű ellenőrizni, hogy

(Ez az azonosság például az x+ i.y alakú komplex számok szorzásából
nyerhető.)
i.y alakú komplex számok szorzásából
nyerhető.)
Ha bebizonyítjuk, hogy az előjelek megfelelő választásával  és
és  egész,
kész vagyunk.
egész,
kész vagyunk.
Tekintsük az xv+yu és xv-yu számok szorzatát:
(xv+yu)(xv-yu)=x2v2-y2u2=(x2v2+dy2v2)-(y2u2+dy2v2)=v2a-y2b;
ez a szám osztható b-bel. Mivel b prím, ebből következik, hogy
az xv+yu és xv-yu számok közül legalább az egyik
osztható b-vel. Mivel x, y, u és v előjelét
tetszés szerint megváltoztathatjuk, feltehetjük, hogy xv+yu
osztható b-vel, vagyis
 egész.
Az (1) egyenletből láthatjuk, hogy ekkor
egész.
Az (1) egyenletből láthatjuk, hogy ekkor
 is egész.
is egész.
B. 3401. Egy nagy, önkiszolgáló raktárban rengeteg árut tárolnak legfeljebb 1 tonnás csomagokban. Van egy 3 és egy 4 tonnás teharautónk. Szerződést akarunk kötni, amelyben vállaljuk, hogy a raktárból egy fordulóval legalább N tonna árut szállítunk el. Mekkora N legnagyobb értéke? (5 pont)
Arany D. versenyfeladat (2000) nyomán
Megoldás. Ha a raktárban csupa egyforma tömegű csomag van és a közös tömeg x, akkor a két teherautóra [3/x] illetve [4/x] darabot rakhatunk fel, vagyis az elszállítható tömeg ([3/x]+[4/x])x=7-({3/x}+{4/x})x. Az f(x)=({3/x}+{4/x})x függvény grafikonját az ábrán láthatjuk.

Legyen 0< <1/5 egy kis
pozitív szám. Ha x=4/5+
<1/5 egy kis
pozitív szám. Ha x=4/5+ ,
akkor a két teherautó összesen 3+4=7 csomagot vihet el, ezek tömege
együttesen 28/5+7
,
akkor a két teherautó összesen 3+4=7 csomagot vihet el, ezek tömege
együttesen 28/5+7 . Ebből
következik, hogy az elvállalt össztömeg nem lehet 28/5-nél nagyobb.
. Ebből
következik, hogy az elvállalt össztömeg nem lehet 28/5-nél nagyobb.
Megmutatjuk, hogy minden esetben elszállíthatunk 28/5 tonnánál több árut.
Mivel a fenti négy lehetőség közül mindig teljesül legalább az egyik, minden esetben el tudunk szállítani 28/5 tonnánál többet.
Az N legnagyobb értéke tehát a 28/5.

