A 2000. novemberi C-jelű matematika gyakorlatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
C. 600. Személygépkocsival utazunk Budapestről Kassa felé állandó sebességgel. Meglátunk egy kilométert jelző táblát, amin egy kétjegyű szám van. Fél óra múlva olyan táblához érünk, amelyen az előbbi számjegyek állnak fordított sorrendben. Újabb 30 perc múlva olyan táblához érünk, amelyen a két eddigi számjegyen kívül még egy 0 is van. Mekkora sebességgel haladunk?
Megoldásvázlat. Ha az első szám ab, akkor a második ba, a harmadik számra pedig négy lehetőség van: I) a0b, II) ab0, III) b0a vagy IV) ba0. Mind a négy esetben egy egyenletet kell megoldanunk.
I) (10a+b)-(10b+a)=(10b+a)-(100a+b) 9(a-b)=9(-11a+b)
6a=b
a=1, b=6. A három szám, amit a kilométertáblákon láttunk:16, 61 és 106.
II) 9(a-b)=(10b+a)-(100a+10b) 9(a-b)=9(-11a), amit egyetlenegy 1 és 9 közé eső szám sem elégít ki.
III) 9(a-b)=(10b+a)-(100b+a)=9(-10b), ami megint ellentmondás.
IV) 9(a-b)=(10b+a)-(100b+10a)=9(10b-a) 2a=11b, tehát a legalább 11, ami nem lehet.
Tehát az egyetlen megoldás az I) esetben kapott három szám, amiből a sebesség (106-16)km/h=90km/h.
C. 601. Oldjuk meg a következő egyenletet:
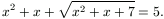
Javasolta: Gyanta Nándor, Budapest
Megoldásvázlat. Legyen y=x2+x+7. Ekkor az egyenlet a következőképpen néz ki: y−7+√y=5, √y=12−y, amiből négyzetreemeléssel y=144-24y+y2. Ebből y=16 vagy 9. A 16 hamis gyök, a 9 jó. x2+x+7=9 egyenletből x=1 vagy x=-2, mindkét gyök jó.
C. 602. Legkevesebb hány egységkockából lehet összerakni egy nagy kockát úgy, hogy belül legyen a kis kockáknak több, mint a fele?
Megoldásvázlat. A feltételek szerint, ha a nagy kocka d élű, akkor (d-2)3ged3/2. Ebből átalakítással d(d2-12d+24)ge16. Mivel a d2-12d+24 kifejezés d=6−2√3<3-ra illetve \displaystyle d=6+2\sqrt9">-re veszi föl a 0-t, ezért 3 és 9 között negatív, és 10-től kezdve monoton nő. 10-re pedig teljesül az egyenlőtlenség, tehát legkevesebb 1000 egységkocka kell ahhoz, hogy a feladat feltétele teljesüljön.
C. 603. Határozzuk meg az f(x)=(x2+x+1)/(x2+1) függvény értékkészletét.
Megoldásvázlat. y=x2+x+1x2+1=1+xx2+1. Ebből 0=x2−1y−1⋅x+1. A függvény értékkészlete megegyezik azokkal az y értékekkel, amelyekre ennek az egyenletnek van gyöke, azaz D=(1y−1)2−4≥0. Azaz, ha (1y−1)2≥4.
I) 1y−1≥2
a)y>1, ekkor 1ge2y-2, azaz 3/2gey>1.
b)y<1, ekkor 1le2y-2, azaz yge3/2, ami ellentmondás.
II) 1y−1≤−2
a) y>1, ekkor 1le-2y+2, amiből 1/2ley, ami ellentmondás.
b) y<1, ekkor 1ge-2y+2, ebből 1/2ley<1.
Összegezve: 1/2ley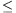 3/2, de y≠1.
3/2, de y≠1.
C. 604. Az ABC háromszög beírt körének középpontja O, területe pedig t. Mutassuk meg, hogy
2t=AO2sin +BO2sin
+BO2sin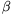 +CO2sin
+CO2sin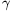 .
.
Javasolta: Mihalovics Sándor, Esztergom
Megoldásvázlat.

Jelölje a beírt kör oldalakkal való érintési pontjait rendre A', B', C'. Az AC'O és az AB'O háromszögekből kirakható az ábrán látható háromszög,

melynek területe 1/2⋅¯AO2sinα. Hasonlóan, a BC'O és a BA'O háromszög területének összege 1/2⋅¯BO2sinβ, illetve a CA'O és a CB'O háromszög együttes területe 1/2⋅¯CO2sinγ. A három terület kétszeresét összeadva pont a bizonyítandó állítást kapjuk.

