A 2000. novemberi számban kitűzött fizika elméleti feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

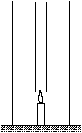P. 3374. Széles, magas üvegcső áll az asztalon. A cső közepén alul egy gyertya ég, a gyertya felett pedig egy keskeny, hosszú üvegcső helyezkedik el, az ábrán látható módon.

a) Mi történik, ha a belső üvegcsövet eltávolítjuk?

b) Mi történik, ha a külső üvegcsövet távolítjuk el? (3 pont)

Becslési verseny, Sárospatak

Megoldás. A belső cső mint kémény működik, a meleg égéstermékek azon távoznak, míg a két cső között a gyertya felé áramlik a friss levegő.

a) Ha eltávolítjuk a belső csővet, a külső megtelik széndioxiddal, és a gyertya elalszik.

b) Ha a külső csövet távolítjuk el, nem történik semmi.

P. 3375. Egy bizonyos folyadék a hajszálcsőben csak félannyira emelkedik fel, mint a víz. Mi történik, ha a vizen úszó zsilettpenge mellé cseppentünk ebből a folyadékból a penge egyik oldalán? (3 pont)

Közli: Kovács Ádám, Budapest, Balassi B. Gimn.

Megoldás. A penge a másik oldal felé elúszik, mert ott a nagyobb felületi feszültségű víz jobban húzza, mint a becseppentett (kisebb felületi feszültségű) folyadék.

P. 3376. Egy kirándulócsoport egyik tagja, András, kissé gyorsabban halad, mint a korábban induló, de lassabb Béla. András megfigyeli, hogy mikor halad el Béla egy jellegzetes fa mellett, s karórája segítségével megméri, hogy ő t₁ idő múlva ér a fához, majd ezután t₂ idő múlva éri utól Bélát. Azt állítja, hogy e két időadat segítségével ki tudja számítani sebességeik v_A/v_B arányát. Hogyan? (3 pont)

Közli: Gnädig Péter, Budapest

Megoldás. Legyen a fa és a találkozási pont távolsága s! Nyilván s=(t₁+t₂)v_B, de s=t₂v_A is! Ebből

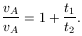
P. 3377. Egy 80 kg tömegű súlylökő álló helyzetből a vízszintessel 45^o-os szöget bezáró irányban, egyenletesen gyorsítva 0,1 másodperc alatt löki el a 6 kg-os vasgolyót. A golyó a talajtól 2 méterre van akkor, amikor elhagyja a súlylökő kezét, és 2 másodperc múlva ér földet. Legalább mekkora a tapadási súrlódási együttható, ha a súlylökő nem csúszik meg dobás közben? (5 pont)

Közli: Farkas László, Keszthely

Megoldás. Jelölje a hajítás szögét (ez most 45^o), induljon a golyó h(=2 m) magasságból, és repüljön t(=2 s) ideig! Jelölje továbbá a tömegeket M(=80 kg) és m(=6 kg), végül legyen a gyorsítás ideje 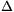t(=0,2 s)! A hajítás sebessége

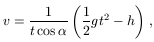
így a golyó gyorsulása az ellökés alatt

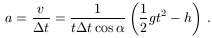
Ennek megfelelően a talajt nyomó függőleges erő N, és a súrlódási erő S:

N=(M+m)g+(m+m')asin ,    S=(m+m')acos .

Itt az m' effektív tömeggel azt vesszük figyelembe, hogy nem csak a golyó, de a súlylókő karja is gyorsul. A fentiek alapján

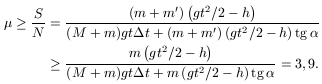
P. 3378. Feltöltött síkkondenzátor lemezei 3 cm-re vannak egymástól. Betolunk közéjük egy 3 mm vastag, töltetlen fémlemezt. Megváltozik-e a kondenzátor feszültsége és energiája? Kell-e munkát végezni a lemez betolása közben? (4 pont)

Közli: Radnai Gyula, Budapest

Megoldás. Ha az eredetileg D távolságra levő lemezek kőzé egy d vastagságú fémlemezt tolunk, eredményül két sorba kötött kondenzátort kapunk, melyek lemeztávolságai rendre D₁ és D₂ úgy, hogy D₁+D₂=D-d. Az eredő kapacitás az eredeti C kapacitás D/(D-d)-szerese. (Ez ugyanolyan, mintha a lemezek eredeti D távolságát d-vel csökkentettük volna.) A lemez betolásakor a kondenzátoron tárolt Q töltés nem változik, így az U=Q/C és W=Q²/2C összefüggések alapján mind a feszültség, mind az energia (D-d)/D-ed részére csökken. Így a lemez betolásakor nem kell munkát végeznünk, a kondenzátor végez munkát a lemezt tartó erő(nk) ellenében.

A kondenzátor tehát mintegy behúzza a lemezei közé a vastag fémlemezt. A fémdarabra ható erőnek azért lehet a lemezek síkjával párhuzamos összetevője, mert a kondenzátor elektromos mezője a lemezek szélénél nem merőleges a lemezekre, hanem kifele ,,dudorodik'', s ez az erőtér a betolt (összességében semleges, de megosztás révén polarizálódott) fémdarabra erőt képes kifejteni. Ha - naív módon - a kondenzátor elektromos mezőjét mindenhol ugyanakkorának és a lemezekre merőlegesnek tekintenénk, azt a hibás következtetést vonhatnánk le, hogy a fémdarabra nem hat erő, így az munkavégzés nélkül betolható a kondenzátor lemezei közé, illetve kihúzható onnan.

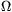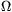P. 3379. A 100 , 200 , 300 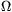 és 400  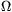ellenállású fogyasztókat úgy kapcsoljuk össze, hogy összesen 100 W teljesítményt vesznek fel, ha 100 V-ra kapcsoljuk a rendszert. Mekkora teljesítményt vesznek fel ekkor a fogyasztók külön-külön? (4 pont)

Közli: Varga István, Békéscsaba

Megoldás. A kérdéses kapcsolásban a 100 ohmos és a 300 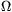-os ellenállások sorba, az így kapot 400 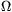-os, az eredei 400 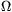-os és a 200 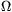-os ellenállások pedig párhuzamosan vannak kötve. A felvett teljesítmények L₁₀₀=6,25 W, L₃₀₀=18,75 W, L₄₀₀=25 W és L₂₀₀=50 W.

P. 3380. Pontszerűnek tekinthető fényforrást helyezünk el egy 8,4 mm vastag üvegtábla mellett. A fényforrás oldaláról, az üvegre majdnem merőlegesen nézve több tükörképet is látunk, melyek egymástól 12-12 mm-re vannak. Határozzuk meg az üveg törésmutatóját! (5 pont)

Közli: Kotek László, Pécs

Megoldás. A képek a fényforráson átmenő, az üveg síkjára merőleges egyenes mentén láthatók. Az első képet adó sugarak az üveg tárgy felőli oldaláról egyszerűen visszaverődnek, a második kép úgy keletkezik, hogy a sugarak az üvegbe belépve megtörnek, a tárgy felől nézve hátsó oldalon visszaverődnek, majd egy újabb töréssel az első oldalon - az első képet alkotó sugarakkal párhuzamosan, de azokhoz képest eltolva - kilépnek. Álltalában az m-edik kép esetében a sugarak (2m-2)-szer járják meg az üveget oda-visza verődve mielőtt újra kilépnének. 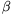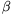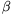Ha az üveg d vastagságú, beesési és törési szög mellett az egymást követő képekhez tartozó sugarak az üvegből egymastól s=2dtg  távolságra lépnek ki, így az egymás utáni képek távolsága x=s/tg =2d tg /tg . 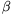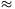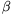Kis szögek esetén tg /tg sin /sin =1/n. Innen a törésmutató n=2d/x=1,4.

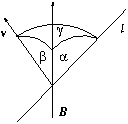
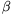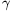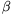P. 3381. B indukciójú homogén mágneses mezőben l hosszúságú, v sebességű egyenes vezető mozog. Mekkora feszültség keletkezik a vezeték két vége között, ha a vezeték a mágneses indukcióval , az indukció a sebességgel , a sebesség a vezetékkel szöget zár be? (Legyen pl. =30^o, =40^o, 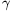=50^o, l=0,5 m, v=2m/s és B=0,5 mT.) (5 pont)

Közli: Holics László, Budapest

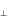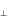I. megoldás. A keresett feszültség U=Blv, ahol l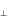 a vektronak tekintett (a vezetővel megegyező irányú és annak hosszával azonos nagyságú l-nek a B-re, v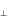 pedig a v-nek mind az l-re, mind a B-re merőleges komponense. (Nyilván ugyanezt adja mondjuk az lv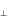B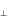 szorzat is, ahol most v 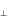az v-nek az l-re, B 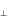pedig a B-nek mind az l-re, mind a v-re merőleges komponense.)

Legyen a közös O pontból felrajzolt v, B és l vektorok végpontja rendre V, B és L, továbbá a V és L pontok vetülete a B-re merőleges síkra V^' és OL^'! Az OV^' és OL^' szakaszok hossza rendre vsin 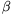 és lsin .

A keresett indukált feszültség:

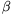U=Blvsin sin sin '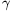

ahol a 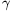^' az OV^' és OL^' egyenesek által bezárt szög. Mivel a VL hossza

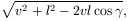
a V^'L^' hossza (Pitagorasz tétele szerint, v és l vektorok B irányú vetületének ismeretében)

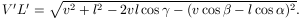
Ennek segítségével a V^'OL^' háromszögre felírt koszinusz-tétel szerint

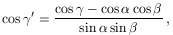
így (némi átrendezés után)

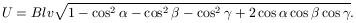
Numerikusan: U=0,16 mV.

2. megoldás. Vegyük fel a koordináta-rendszert úgy, hogy B jelölje ki az x tengelyt, l pedig feküdjön az x-y síkban! Ekkor e vektorok komponensei rendre (B,0,0) és (lcos ,lsin , 0). (Nyilván l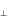=lsin .) A v vektor (v_x,v_y,v_z) komponenseire (melyek közül v_z=v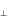) a következő egyenleteket írhatjuk fel:

v.b=vxB=vBcos 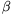, v.l=vxlcos +vylsin =vlcos 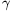, v.v=vx2+vy2+vz2=v2.

Felhasználtuk, hogy két tetszőleges vektor skaláris szorzását a nagyságuk és a közbezárt szögük segítségével is kiszámíthatjuk, de a komponenseik felhasználásával is meghatározhatjuk:

a^.b=|a||b|cos 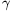=a_xb_x+a_yb_y+a_zb_z.

Az egyenletrendszert v_z-re megoldva az U=Blsin v_z feszültségre az I. megoldásban megadott eredményt kapjuk.

---

P. 3382. Szilárd Leó és Walter Zinn megmérte, hogy az ²³⁵U-ból hasadásonként átlagosan 2,5 neutron keletkezik. Tekintsünk egy képzeletbeli reaktorban 100 maghasadást. Az ezekből létrejött neutronok közül 10 kiszökik a reaktorból, 8 befogódik az ²³⁸U-ban, valamennyit elnyelnek a szabályozórudak, a többi pedig ismét hasít. A neutronok hány százalékát kell elnyelniük a szabályozórudaknak, hogy a neutronok száma időben ne változzék? (3 pont)

Szilárd Leó országos nukleáris verseny, Paks

Megoldás. 100 maghasadásból 250 neutron keletkezik, ezek közül - stacionárius (állandósult) állapotban - 100-nak kell újra hasítania. Ehhez a szabályzórudaknak 250-(100+10+8)=132 neutront kell elnyelniük, azaz a keletkező neutronok 53%-át.

Megjegyzés: A feladat eredeti - a Szilárd Leó versenyen közölt - szövege szerint a keletkező neutronokból 8 a hűtővízben nyelődik el, 40 pedig az ²³⁸U-ban. Ezekkel a reálisabb adatokkal a feladat numerikus megoldása módosulna: a szabályzórudaknak 250-(100+10+8+40)=92 neutront kellene elnyelniük, ez a keletkező neutronok 37%-a.

---

P. 3383. Egy vékony, hosszú üvegcső belseje a hosszának felében kormozott, másik fele pedig tükröző. A csövet függőlegesen, fekete felével lefelé az asztalra állítjuk (lásd az (a) ábrát). Az asztalon, a cső tengelyénél pontszerűnek tekinthető D fotodetektor van. Hányszor nagyobb értéket mutat a fotodetektor, ha a csövet a (b) ábrán látható helyzetbe fordítjuk? (5 pont)

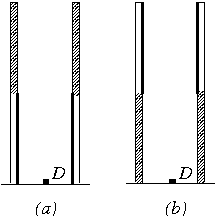
Román versenyfeladat

Megoldás. Legyen a cső hossza 2l, a sugara pedig r! A kérdéses pontban mérhető megvilágítás arányos azzal a térszöggel (egységsugarú gömb felületére vetített terület nagyságával), amelyben kinézve az ,,ég'' látszik.

Az első esetben a teljes tükröző felület helyén is az ég látszik, ezért J₀=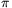(r/l)², ahol az az ég fényességétől függő arányossági tényező. (Kihasználtuk, hogy l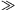r.)

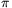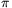A második esetben a kérdéses térszög két részből áll. Az egyik az amelyben az ég dirrekt látható, ez (r/2l)², a másik az, amelyben a tükröző felület felső harmada látszik, ez ((3r/2l)²-(r/l)²). Így a második esetben a megvilágítás