A 2000. decemberi számban kitűzött fizika elméleti feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3384. Egy téglatest alakú edénybe vizet öntünk. Mekkora az edény magassága, ha mindegyik oldallapra a víz súlyánál nagyobb erő hat? (3 pont)

Lánczos Kornél verseny, Székesfehérvár

Megoldás. Ha az alaplap oldalai a és b, az edény magassága pedig h, az oldalakra ható erő h²a/2 és h²b/2, míg a sűrűségű folyadék súlya abh. Innen h2max(a,b).

P. 3385. Egy 3 m hosszú, méterenként 1 kg tömegű, az asztalon fekvő lánc egyik végére egy 2 dm élű, 2700 kg/m³ sűrűségű alumíniumkockát erősítünk. A kockát megfogjuk, s egyenletesen emeljük 0,5 m/s sebességgel. Mekkora a helyzeti energia változása a) 5 másodpercnyi, b) 10 másodpercnyi emelés után? (3 pont)

Jedlik Ányos verseny (6. és 7. osztály), Nyíregyháza

Megoldás. a) A láncnak 5^.0,5=2,5 m hosszú darabja emelkedik fel, ennek tömegközéppontja 1,25 m magasra kerül. Az alumíniumkocka tömege 2^3.2,7=21,6 kg, ezt emeljük 2,5 m magasra. A rendszer helyzeti energiájának változása

(21,6^.2,5+2,5^.1,25)^.9,81=0,56 kJ.

b) Most a lánc felső vége (és az alumíniumkocka) 5 m, az alja 2 m magasra kerül, a lánc tömegközéppontja tehát 3,5 m-t emelkedik. A lánc helyzeti energiájának változása 3^.3,5^.9,81=103 J, az alumíniumkockáé 21,6^.5^.9,81=1060 J, a teljes energiaváltozás pedig 1,16 kJ.

Megjegyzés: Érdemes megfontolni, hogy az emelés közben végzett munka sem az a), sem a b) esetben nem egyezik meg a helyzeti energia változásával, hiszen a rendszer (vagy annak egy része) mozgási energiára is szert tesz. Meglepő módon a végzett munka még a helyzeti és a mozgási energia változásának összegénél is nagyobb, aminek az az oka, hogy a lánc emelése közben a láncszemek rugalmatlan ütközések sorozatán keresztül tesznek szert sebességre, s az ütközéseknél hő fejlődik.

P. 3386. Hővezető, merev fal oszt két egyenlő részre egy 3 liter térfogatú, hőszigetelt falú tartályt. Mindkét részben 10⁵ Pa nyomású, 300 K hőmérsékletű oxigén van: a bal oldaliban kétatomos (O₂), a jobb oldaliban háromatomos (O₃), vagyis ózon. Az ózon egy idő után kétatomos oxigénné alakul át úgy, hogy két ózonmolekulából három O₂ molekula keletkezik: 2O₃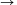3O₂.

a) Mennyi a két részben levő oxigénatomok számának aránya?

b) Mennyi lesz a nyomás és a hőmérséklet az egyes tartályrészekben a termikus egyensúly beállta után, ha minden egyes O₃ molekula átalakulása 2,4^.10^-19 J energiafelszabadulással jár?

(Tekintsük az O₃-at 6, az O₂-t 5 szabadsági fokú ideális gáznak!) (4 pont)

Bethlen Gábor verseny, Hódmezővásárhely

Megoldás. a) A pv=nRT összefüggésből következően a mólok n száma azonos a két oldalon, tehát az atomok számának aránya 2 : 3.

b) A belső energiának a hőmozgásból származó (a kémiai kötési energiát nem tartalmazó) része kezdetben , az átalakulás után pedig . A kettő különbsége a felszabaduló kémiai energia nN_A^.E (ahol N_A=6^.10²³ az Avogadro szám, és E=2,4^.10^-19 J), azaz

Innen

P. 3387. Miért izzadnak sportolás közben a gyerekek általában kevésbé, mint a felnőttek? (4 pont)

Közli: Simon Péter, Pécs

Megoldás. A sportolás (gyors mozgás) közben termelt hő az emberi test tömegével, azaz a térfogattal arányos, a hőleadás viszont a felülettel. Mivel a gyermek kisebb, az egységnyi térfogatra jutó felülete nagyobb, így kevésbbé intenzív izzadásal is képes a szükséges hőt leadni.

P. 3388. Az 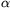hajlásszögű deszkán m tömegű testet csúsztatunk fel egyenletes mozgással. Határozzuk meg a csúsztatáshoz szükséges minimális erő nagyságát és irányát! A súrlódási tényező 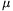. (5 pont)

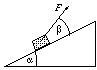
Közli: Rácz György, Mezőkövesd

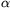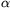I. megoldás. A ládát toló F erő iránya az ábrának megfelelően szöget zár be a lejtővel. Jelölje azt az erőt amivel a láda a lejtőt nyomja N, a súrlódási erőt S, a súrlódási határszöget pedig ₀ (ahol tg₀=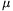). Az erők egyensúlya miatt

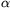F=mgsin+S,

N=mgcos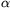-Fsin,

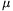S=&N.

Innen

Ez nyilván akkor a legkisebb, ha =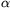₀. Ekkor

Megoldásunk akkor helyes, ha F még nem függőleges, és a ládát nem emeljük el a lejtőtől (N pozitiv). Érdekes módón a két feltétel konkrétan megfogalmazva ugyanarra az egyenlőtlenségre vezet: cos(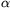+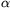₀)>0. Ha ez nem teljesül, a legkönnyebb a ládát a lejtő elhagyásával egyszerűen felemelni.

II. megoldás. A test csúszik, tehát a talaj N nyomóerejének és az S súrlódási erőnek az eredője rajta fekszik a súrlódási határszög által kijelölt (vagyis a test pillanatnyi helyzetét megadó T ponton átmenő, a lejtő normálisával ,,balra'' 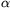₀ szöget bezáró) e egyenesen. Ennek az erőnek és a kérdéses F erőnek vektori összege -mg-t kell adjon, hiszen N+S+F+mg=0.

Az F erőt úgy szerkeszthetjük meg, hogy a -mg vektor P végpontját összekötjük az e egyenes valamely Q pontjával. Az erő F nagysága akkor a legkisebb, ha PQ minimális, vagyis amikor PQ merőleges TQ-ra. Az ábráról leolvasható, hogy PQ optimális esetben a vízszintessel 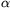+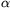₀ szöget zár be, a minimális nagyságú erő és a lejtő síkjának szöge tehát =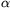₀. A minimális erő nagysága

Mindez csak akkor igaz, ha Q a T ponttól ,,balra'' helyezkedik el, vagyis amíg +₀</2. Ellenkező esetben F legkisebb értéke mg, iránya pedig függőlegesen felfele mutat.

P. 3389. A m és M tömegű, gömb alakú testeket elhanyagolható tömegű csigán átvetett súlytalan fonal köti össze. A két testet az ábrán látható helyzetben tartjuk, és egy adott pillanatban mindkettőt elengedjük. A M tömeg sokkal -- pl. ezerszer -- nagyobb, mint m. Az asztallap és a m tömegű test között a súrlódás elhanyagolható. Elválik-e az elengedést követő pillanatban a m tömegű test az asztallaptól? (5 pont)

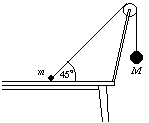
Közli: Károlyházy Frigyes, Budapest

Megoldás. A nagyobb test gyakorlatilag szabadon, g gyorsulással esik. Tételezzük fel, hogy a m tömegű test nem válik el az asztallaptól, vagyis hogy a kis test vízszintesen mozog bizonyos a kezdeti gyorsulással. A fonalnak az asztalon levő vége vízszintes irányban ugyancsak a gyorsulással kezd el mozogni, és ennek a gyorsulásnak fonal irányú vetülete acos 45^o, melynek meg kell egyeznie a M tömegű test g gyorsulásával, hiszen a fonal nyújthatatlan. Ezek szerint a=g, a kis testre ható vízszintes irányú erő pedig F_v=ma=mg. Mivel ezt az erőt csak a fonal fejtheti ki, a benne ható erő F=F_v=2mg, melynek függőleges komponense F_f=mg. Ez az erő nagyobb, mint a m tömegű test súlya, tehát a kis test - feltevésünkkel ellentétben - elválik az asztallaptól.

P. 3390. Mekkora legyen az ábrán látható kapcsolásban a C kapacitás, hogy ebben a kondenzátorban a lehető legtöbb energia halmozódjék fel? Mekkora ez a maximális energiamennyiség? (5 pont)

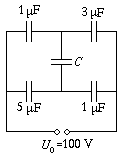
Közli: Légrádi Imre, Sopron

Megoldás. Jelölje a felső ágban található kapacitásokat C₁(=1 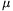F) és C₂(=3 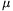F), az alsó ágban levőket pedig C₃(=5 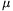F) és C₄(=1 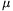F). A Kirchhoff-féle (hurok és csomóponti) törvényekből a C kapacitás töltése

tehát az energiája

Ez egy

tipusú kifejezés, mely a számtani és mértani közép viszonyából következően akkor maximális, ha , azaz C=/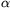. Konkrétan

azaz

Adatainkkal C_opt=2,4 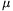F és E_max=1,02^.10^-5 J.

Megjegyzés: A kapcsolás a C kapacitású kondenzátor szempontjából helyettesíthető egy alkalmasan választott U^* feszültségű teleppel és egy vele sorbakapcsolt megfelelő C^* kapacitású kondenzátorral. A két szélsőséges határesetből (nagyon kicsire, illetve nagyon nagyra választva C-t) leolvashatjuk, hogy

illetve

A helyettesítő kapcsolással sorosan kötött C kapacitású kondenzátor energiája akkor lesz a legnagyobb, ha C=C^*, a tárolt energia pedig C^*U^*2/8, numerikusan a fent megadott értékek.

P. 3391. Az ábrán látható d=4 cm szélességű, B=0,02 T indukciójú homogén mágneses mezőbe 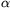=30^o belépési szög alatt, a B vektorra merőlegesen érkezik egy elektronnyaláb.

a) Lassú vagy gyors elektronok tudnak áthaladni a mágneses mezőn?

b) Mekkora feszültséggel gyorsított elektronok ,,verődnek vissza'' a mágneses mezőről? (5 pont)

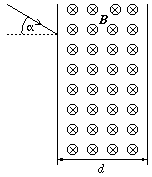
Közli: Varga István, Békéscsaba

Megoldás. A mágnenses térbe belépő elektronok köríven mozognak, a pálya sugarát az

azaz

egyenlet adja meg.

a) Látszik, hogy a gyors elektronok pályasugara nagy, tehát ezek a részecskék átjutnak. Azok az elektronok nem jutnak áta mágneses mézőn, amelyek pályasugara (a geometria alapján) r<2d, azaz amelyekre

mv<2deB.

Ebben a kifejezésben az m helyett az m₀ nyugalmi tömeget használva v=2,8^.10⁸ m/s adódik. Ez több mint a c fénysebesség 90%-a, tehát az

relativisztikus tömegképletet kell használni. Ebből a visszavert elektronok sebességére

adódik.

b) Az elektronok gyorsításkor mc²-m₀c² energiát kapnak, tehát a visszavert elektronokat gyorsító feszültség

P. 3392. Az ábrán látható soros RLC körben az izzó világít. Azt tapasztaljuk, hogy ha rövidre zárjuk a tekercset, nem változik meg az izzó fénykibocsátása. Hogyan változik az izzó fénykibocsátása, ha a kondenzátort zárjuk rövidre? (4 pont)

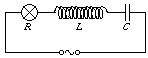
Közli: Nagy Márton, Sopron

Megoldás. Az RLC kör teljes ellenállása

így az R ohmikus ellenállású izzó teljesítménye

A tekercs rövidre zárása esetén

ha tehát P=P', akkor

Feltételezve, hogy a tekercs nem zárlatos (L0), csak

lehet, így a kapacitás rövidre zárásakor

Innen

tehát az izzó elhalványul.

P. 3393. Homogén, egyenletes keresztmetszetű ellenálláshuzalból szabályos tetraédert állítottunk össze. Egy hosszú, egyenes, a tetraéder O középpontjába irányuló vezetéken az A csúcshoz I áramot vezetünk, a B csúcsból pedig hasonló módon elvezetjük. Mekkora és milyen irányú lesz a mágneses indukcióvektor a tetraéder középpontjában? (6 pont)

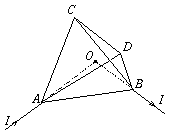
Közli: Radnai Gyula, Budapest

Megoldás. Az elrendezésben a C és a D pontok teljesen szimmetrikus szerepet töltenek be, emiatt ekvipotenciálisak, közöttük nem folyik áram. Az ACB és ADB ágak ellenállása kétszerese az AB ág ellenállásának, így a megfelelő áramerősségek:

,

A Biot-Savart-törvény szerint egy véges hosszúságú egyenes vezetődarab járuléka az általa létrehozott mágneses mezőhöz arányos a vezetékben folyó árammal, és a mező iránya valamely O pontban merőleges arra a síkra, amely vezetőre és az O pontra illeszkedik. Így például az AC szakasz járuléka az O pontbeli mágneses indukcióvektorhoz

B_AC=kI,

ahol k (a tetraéder méretétől is függő) pozitív szám. (Felhasználtuk, hogy a szabályos tetraéder szemközti élei merőlegesen egymásra, így a vektor éppen a Biot-Savart-törvénynek és a jobbkéz-szabálynak megfelelő irányú.) A többi él járuléka is hasonlóan számolható, és mivel a két hosszú egyenes vezető a középpontban nem hoz létre mágneses teret, a teljes mágneses indukció az O pontban:

B=kI(++++).

Ez a vektor viszont

+==-

és

+==-.

miatt nullvektor, vagyis a mágneses indukció a tetraéder középpontjában nulla.