A 2001. februári B-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
B. 3432. Az alábbi táblázat a Pascal-háromszög mintájára készült. Az első sor két eleme 1 és 2, ezután pedig minden újabb szám a felette álló kettő összege.
| 1 | 2 | |||||||
| 1 | 3 | 2 | ||||||
| 1 | 4 | 5 | 2 | |||||
| 1 | 5 | 9 | 7 | 2 | ||||
a) Mennyi a 100-adik sorban álló számok összege?
b) Mit kapunk, ha a 100-adik sorban váltakozó előjellel adjuk össze a számokat?
c) Mennyi a 100-adik sor 47-edik eleme? (4 pont)
Megoldás. a) Mivel a 2. sortól kezdve minden szám a felette levő két szám összege, így minden szám pontosan két helyen szerepel az alatta levő sorban összeadandó tagként. Tehát minden sorban a számok összege kétszer akkora, mint a felette levő sorban. Mivel az első sorban 3 a számok összege, ezért a 100. sorban 3.299.
b) Mivel minden szám két szomszédos számban szerepel az alatta levő sorban, ezért egyszer negatív, egyszer pedig pozitív előjellel vesz részt az összegben. Így a második sortól kezdve minden sorban az összeg 0 lesz.
c) A táblázatot megkaphatjuk két Pascal háromszög egymásra csúsztatásával is.
Így a 100. sor 47. eleme megegyezik a Pascal háromszög 100. sorában a 47. elem és a 99. sorában a 46. elem összegéval, azaz egyenlő ((10046)+(9945))-tel.

B. 3433. Egy geometria konferencia résztvevői a szünetben olyan szendvicseket kaptak, amelyek mindegyikén egy téglatest alakú kenyéren egy vastag szelet henger alakú sajt és egy gömb alakú húspogácsa volt. Mindig ketté lehet-e vágni egy ilyen szendvicset egyetlen egyenes vágással úgy, hogy a két rész kenyérből, húsból és sajtból is ugyanannyit tartalmazzon? (4 pont)
Megoldás. Igen. A téglatest szimmetriaközéppontján átmenő síkok felezik a téglatest térfogatát. Hasonlóan a gömb ill. a henger szimmetriaközéppontján átmenő síkok is felezik a gömb ill. a henger térfogatát. Tehát ha olyan sík mentén vágjuk ketté a szendvicset, ami átmegy mindhárom test szimmetriaközéppontján (ilyen mindig van), akkor az felezi mind a kenyér, mind a hús, mind a sajt térfogatát.
B. 3434. Egy trapéz alapjai a és b. A trapéz elmetszhető az alapokkal párhuzamos egyenessel úgy, hogy a két rész-trapézba kör írható. Mekkora az eredeti trapéz kerülete? (3 pont)
Javasolta: Reményi Gusztáv, Budapest
Megoldás. A CDFE és az EFAB trapézok hasonlóak egymáshoz (hiszen AB∥CD∥EF, CE∥EB, DE∥EA, és mindkettőbe kör írható). Tehát ac=cb, amiből c=√ab. Mivel egy érintőnégyszög szmeközti oldalainak összege egyenlő, ezért a két trapéz kerülete felírható 2(a+c) ill. 2(b+c) alakban. Az eredeti trapéz kerületét úgy kaphatjuk meg, hogy a két tarpéz kerületének összegéből levonunk 2c-t, hiszen c-t egyszer sem kellett volna beleszámolnunk az összegbe. Így a kerület 2(a+c)+2(b+c)−2c=2(a+b+c)=2(a+b+√ab).

B. 3435. Keressük meg az alábbi egyenletrendszer nemnegatív megoldásait:
x1+x2+x3+...+x100=5050
x22-x12=3, ..., xk2-xk-12=2k-1, ..., x1002-x992=199.
(4 pont)
Megoldás. Nyilván xi=i (i=1,2,...,100) megoldása az egyenletrendszernek. Indirekt módon bebizonyítjuk, hogy más megoldás nincs. Legyen ugyanis x1=1+m, ahol mne0. Teljes indukcióval belátjuk, hogy ekkor xi2=i2+m. Az állítás n=1-re igaz. Tegyük föl, hogy n=k-ra igaz. xk+12=2(k+1)-1+xk2=2(k+1)-(k2+m), amiből xk+12=(k+1)2+m.
Mivel 5050 pont az első száz pozitív egész szám összege, ezért az első egyenletből √12+m2+√22+m2+...+√1002+m2=√12+√22+...+√1002 következik. Ha -1lem<0, akkor az egyenlet baloldalának minden egyes tagja kisebb, mint a neki megfelelő jobboldali tag; ha pedig m>0, akkor nagyobb, így a tagok összege sem lehet egyenlő a jobboldalon levő tagok összegével. Így azt kaptuk, hogy más megoldása valóban nincs az egyenletrendszernek.
B. 3436. Az egységnyi területű ABC háromszög AB, BC, CA oldalain adottak a C1, A1, B1 pontok úgy, hogy
AC1/C1B=1/2,
BA1/A1C=1/3,
CB1/B1A=1/4.
Mekkora területű háromszöget határolnak az AA1, BB1, CC1 egyenesek? (3 pont)
Megoldás. Tekintsük az ábrát! A piros színnel behúzott szakaszok párhuzamosak a megfelelő oldalakkal. Ekkor TAC1D=1/4.1/3.2/5=1/30, TBA1E=1/5.5/17.1/4=1/68, TcB1F=1/3.1/5.3/11=1/55. Ebből TC1BED=1/4-1/30-1/68=103/510, TA1CFE=1/5-1/68-1/55=125/748, TB1ADF=1/3-1/30-1/55=31/110. Így TDEF=1-1/30-1/68-1/55-103/510-125/748-31/110=529/1870.

B. 3437. Egy egyenesen ebben a sorrendben adottak az A, B, C, D pontok úgy, hogy BC=2AB, CD=AC. Bizonyítsuk be, hogy bárhogyan is rajzolunk egy-egy kört az A és C, illetve a B és D pontokon keresztül, akkor ezek közös húrja felezi az AC szakaszt. (4 pont)
Megoldás. Rajzoljunk föl tetszőlegesen egy-egy kört A, C ill. B, D köré, és jelöljük M-mel a két kör közös húrja, valamint az egyenes metszéspontját. Mivel M rajta van a közös húron, ezért a két körre vonatkozó hatványa megegyezik: AM.MC=BM.MD. Felhasználva a feltételeket az egyenlet átalakítható: AM.(3AB-AM)=(AM-AB)(6AB-AM), amiből AM=32AB, tehát M felezi az AC szakaszt.

B. 3438. Az f(x,y,;z) függvényre teljesül, hogy bármely t valós számra
f(x+t,y+t,z+t)=t+f(x,y,z);
f(tx,ty,tz)=tf(x,y,z);
f(x,y,z)=f(y,x,z)=f(x,z,y).
Mennyi f(2000, 2001, 2002)? (5 pont)
Megoldás. f(1,0,-1)=-1.f(-1,0,1)=-f(-1,01), valamint f(-1,0,1)=f(0,-1,1)=f(0,1,-1)=f(1,0,-1). Tehát f(-1,0,1)=-f(-1,0,1), ami csak akkor lehet, ha 0. f(2000,2001,2002)=f(2001+(-1),2001+0,2001+1)=2001+f(-1,0,1)=2001+0=2001.
B. 3439. Jelöljön p egy pozitív számot, és tekintsük az 1, p, 1/p, p2, 1/p2, ..., pn, 1/pn ... végtelen sorozatot. Mely p számokra igaz, hogy minden pozitív szám tetszőleges pontossággal megközelíthető a fenti sorozat véges sok alkalmas elemének összegével? (5 pont)
Megoldás. Az állitás nyilván nem igaz, ha p=1, a továbbiakban a szimmetria miatt föltesszük, hogy p>1. Pozitív számok egy H halmazát hívjuk ,,egyenletesnek'', ha van olyan d>0, hogy minden pozitív számtól legfeljebb d távolságra található H-beli elem. Megmutatjuk, hogyha 1<ple2, akkor a p természetes kitevőjű hatványaiból készített véges összegek halmaza egyenletes. Ezt az alábbi formában igazoljuk az n-re vonatkozó teljes indukcióval:
ha 0<T<pn, akkor van olyan részhalmaza az (1,p,p2,...,pn-1) halmaznak, amelyben az elemek összege 1-nél kevesebbel tér el T-től.
Ha n=0, akkor 0<T<1 és így az üres halmaz -- amelyben az elemek osszege 0 -- megfelelő. Legyen most n>0 es tegyük fel, hogy az állítás igaz minden n-nél kisebb pozitív egészre. Ha T<pn-1 is teljesül, akkor az állítás az indukciós feltevés szerint igaz. Ha pn-1<T<pn, akkor 0<T-pn-1<pn-pn-1=pn-1.(p-1)lepn-1, hiszen ple2. Így a T-pn-1 mennyiségre alkalmazható az indukciós feltevés és így a bizonyítást befejeztük. Legyen most t>0 teszőleges és tekintsük a T=pN.t számot. A fentiek szerint ehhez létezik a p különböző nemnegatív hatványainak egy véges halmaza úgy, hogy ezek S összegére |T-S|<1. Ezt az egyenlőtlenséget pN-nel osztva kapjuk, hogy |t-S/pN|<1/pN. Mivel 1pN tetszőlegesen kicsi lehet, továbbá SpN a kívánt alakú összeg, ezért 1<ple2 esetén bármely pozitív t szám tetszőlegesen megközelíthető e kívánt módon.
Megmutatjuk, hogy ha p>2, akkor ez nem lehetséges. Valóban, ilyenkor a p nemnegatív hatványaiból készített véges összegek halmaza nem egyenletes, a szomszédos elemek közti különbség nem korlátos, így nem hidalható át a p negatív kitevőjű hatványaival, hiszen ezek összege korlátos, p−1+p−2+...=p1−p. A nem egyenletesség pedig következik abból, hogy az első n darab nemnegatív p-hatvány felhasználásával 2n darab összeg készíthető és ezek mindannyian 0 es 1+p+p2+...+pn−1=pn−1p−1 között vannak. A szomszédos számok közti átlagos eltérés eszerint pn−1p−1:2n, ami tart a végtelenhez, ha p>2.
A kívánt előállítás tehát pontosan akkor valósítható meg, ha 1<ple2, vagy pedig a szimmetrikus esetben 1/2<lep<1.
B. 3440. Az A, B, C
pontok tükörképe egy e egyenesre A1, B1,
C1, egy P pontra pedig
A2, B2, C2. Mi a
P tükörképe az e egyenesre, ha 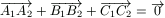 ?
?
3 pont
Megoldás. Indítsunk a P pontból helyvektorokat, és jelöljük ezeket a megfelelő kisbetűkkel. Ekkor a feltétel szerint
a2-a1+b2-b1+c2-c1=0.
De a2=-a, b2=-b és c2=-c, ezért az is igaz, hogy a P-ből a A1A2B1B2C1C2 súlypontjába mutató vektor 0, tehát ez a súlypont egybeesik P-vel. Ez a súlypont megegyezik az A1A2, B1B2 és C1C2 szakaszok felezőpontjai által meghatározott ponthármas súlypontjával is. Ezek a felezőpontok mind rajta vannak az e egyenesen, tehát súlypontjuk is e-n van, azaz P illeszkedik e-re. Tehát P-nek e-re vonatkozó tükörképe önmaga.
B. 3441. Pinokkiónak 9-féle akadályon kell sikerrel túljutnia, hogy hús-vér gyerek lehessen. Nehéz dolga van; ha egy akadályon elbukik, akkor vissza kell térnie az előzőhöz, és ott újra kell próbálkoznia. Ha a legelső akadályon bukik el, akkor fabábu marad örökre. Pinokkió nem tanul a kudarcokból, ezért az egyes akadályokon a siker valószínűsége mindig 1/10, 2/10, 3/10, ..., 9/10, akárhányadszor is próbálkozik. Milyen sorrendben rendezze el a Kékhajú Tündér a Pinokkióra váró akadályokat ahhoz, hogy Pinokkió a legnagyobb eséllyel változzék át igazi gyerekké, és mekkora ebben az esetben a siker valószínűsége? (5 pont)
Megoldás. Legyen az egyes lépések sikerének valószínűsége p1, p2, ..., p9, és annak valószínűsége, hogy az egyes helyzetekből indulva végig tud menni q1, ..., q9, továbbá legyen d0=q1, d1=q2-q1, d2=q3-q2, ..., d8=q9-q8, d9=1-q9. Könnyű végiggondolni, hogy didi−1=1−pipi és d0+...+d9=1.
Ebből
q1=d1=11+1−p1p1+1−p1p1⋅1−p2p2+...+1−p1p1⋅...⋅1−p9p9.
Ha valamelyik i indexre pi<pi+1, akkor a két valószínűséget felcserélve a nevezőben egyetlen tag csökken, a többi nem változik, tehát q1 növekszik. A legnagyobb valószínűség tehát akkor van, ha p1>p2>...>p9, vagyis ha p1=1/10, p2=2/10, ..., p9=9/10. Ezeket az értékeket a fenti képletbe helyettesítve kapjuk, hogy ebben az esetben q1approx0.4315.

