A 2001. márciusi A-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 260. Adott az e egyenesen négy különböző pont:
A, B, C és D, és tudjuk, hogy 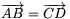 . Létezik-e olyan, egyetlen
egyenes vonalzót használó szerkesztési eljárás, amely egy e-vel
párhuzamos egyenest szerkeszt meg?
. Létezik-e olyan, egyetlen
egyenes vonalzót használó szerkesztési eljárás, amely egy e-vel
párhuzamos egyenest szerkeszt meg?
1. megoldás. Megmutatjuk, hogy a kívánt szerkesztési eljárás nem létezik. Legyen a szerkesztés síkja s, és legyen BC felezőpontja F. Vegyünk fel a térben egy O pontot úgy, hogy az OF szakasz merőleges legyen s-re. Ezen kívül vegyünk fel egy olyan s' síkot, amely nem illeszkedik O-ra és merőleges az e egyenesre.
Az s és s' síkok pontjai között (beleértve az ideális, ``végtelen távoli'' pontokat is) kölcsönösen egyértelmű megfeleltetés az O pontból vetítés; az A, B, C, D pontok képe e vetítés szerint legyen rendre A', B', C' és D'. Könnyen ellenőrizhető, hogy →A′B′=→C′D′.

Tegyük most fel, hogy egy szerkesztési eljárás csak egyenes vonalzó felhasználásával megszerkeszt egy e-vel párhuzamos l egyenest. A szerkesztési eljárás lépéseit O-ból az s' síkra vetítve egy olyan szerkesztési eljárást kellene kapnunk, ami egy, a B'A' egyenessel párhuzamos egyenest szerkeszt meg. Ehelyett azonban l képét, l'-t szerkeszti meg, ami nem párhuzamos B'C'-vel.
Csóka Endre (Debrecen, Fazekas M. Gimn., 10. o.)
2. megoldás. Tekintsük a P(0;-6;0), Q(0;-6;2),
R(0;-6;3) és S(0;-6;6) pontokat. Ezek egy egyenesen helyezkednek
el, és ezt az egyenest tartalmazza a z=-6 sík. Jelöljük ezt a síkot
s-sel. Egy kis számolással ellenőrizhető, hogy POQ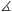 =ROSszog.
=ROSszog.
Vetítsük az origóból a P, Q, R, S pontokat egy olyan, az origóra nem illeszkedő s' síkra, amely merőleges a POS szög felezőjére. Az így kapott pontok legyenek A, B, C és D. Ezek a pontok egy egyenesen vannak, és →AB=→CD. Még az is igaz, hogy az A, B, C, D pontok sorrendje ugyanaz, mint a P, Q, R, S pontok sorrendje.

Tekintsük az s síkban azokat a pontokat, amelyeknek mindhárom koordinátája racionális. Vetítsük ezeket O-ból az s' síkra; így az s' síkban egy V ponthalmazt kapunk. Az s'-beli, racionális koordinátájú pontokat összekötő egyeneseket is vetítsük O-ból az s' síkra; így egy L egyeneshalmazt kapunk. Könnyen meggondolható, hogy a V pont- és a L egyeneshalmaz az s' síknak egy részgeometriáját adja; bármely két V-beli ponthoz létezik pontosan egy olyan L-beli egyenes, amely a két pontra illeszkedik, és bármely két L-beli egyenes metszéspontja, ha létezik, V-beli.
Ha egy szerkesztési eljárás csak az A, B, C, D pontokat és egyenes vonalzót használ az s' síkban, akkor a szerkesztést elvégezhetjük úgy is, hogy csak V-beli pontokat és L-beli egyeneseket veszünk fel, illetve szerkesztünk meg. Ha megmutatjuk, hogy az L halmazban nincs e-vel párhuzamos egyenes, kész vagyunk; a szerkesztési eljárás csak V-beli pontokat és L-beli egyeneseket használva biztosan nem ad e-vel párhuzamos egyenest.
Tekintsünk tehát egy p egyenest az s' síkban, amely e-vel párhuzamos. Azt akarjuk megmutatni, hogy p nincs L-ben. Vetítsük p-t az s' síkra. A p végtelen távoli pontjának képe az s síkban a (-6tg67,5o;0;-6) pont. Mivel tg67.5o irracionális, ebből könnyen látható, hogy p nem köt össze racionális pontokat.
Megjegyzés. A bizonyítás vége elmondható másképpen is. ha tudunk e-vel párhuzamos egyenest szerkeszteni, akkor meszerkeszthetjük BC felezőpontját is. Viszont BC felezőpontja az s-beli (6tg22.5o;0;-6) pont képe, vagyis nincs benne V-ben.
A. 261. Aladár és Benedek egységnyi oldalú szabályos háromszögekből összerakott egy n oldalú szabályos háromszöget. Az így kapott táblán a következő játékot játsszák: Felváltva kiszíneznek egy-egy csúcspontot a piros, kék és zöld színek valamelyikével mindaddig, amíg az összes csúcs, beleértve a nagy háromszög oldalain és belsejében levő pontokat is, ki lesz színezve. Minden olyan egységnyi oldalú háromszögért, amelynek csúcsai piros-kék-zöld színűek pozitív körüljárás szerint, az első lépést megtevő Aladár kap egy pontot. Azokért a háromszögekért, amelyeknek csúcsai piros-kék-zöld színűek negatív körüljárás szerint, Benedek kap egy-egy pontot. Az nyer, aki több pontot szerez.
Kinek van nyerő stratégiája?
Megoldás. Először megmutatjuk, hogy a játék eredménye csak a kerületen levő pontok színezésétől függ. Tegyük fel, hogy már minden pont ki lett színezve. Minden egyes kis háromszögben írjunk számokat az élekhez a következő módon.

Könnyen ellenőrizhető, hogy azokban a háromszögekben, amelyekben vannak egyszínű csúcsok, a számok összege 0. A pozitív körüljárás szerinti piros-kék-zöld háromszögekben a számok összege 1, a negatív körüljárás szerint piros-kék-zöld háromszögekben -1. Az élekhez írt számok összege az egész táblán tehát éppen a pozitív és negatív körüljárás szerint piros-kék-zöld háromszögek számának különbsége, vagyis András és Benedek pontjainak különbsége.
Minden egyes belső él két háromszöghöz tartozik, ezért két számot is írtunk
hozzá. A konstrukció miatt e két szám összege 0. Ezért a belső élekre írt
számok összege 0, és így az összes szám összege megegyezik a határélekhez írt
számok összegével. Ezeket tudva András akkor nyer, ha a tábla határán több 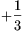 áll, mint
áll, mint 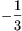 ; Benedek pedig akkor
nyer, ha a határon több −13 áll, mint +13. Azok a határélek, amelyekhez +13-ot írtunk, András sdzámára ,,jók''; azok
pedig, amelyekhez −13-ot írtunk, Bendek számára ,,jók''.
; Benedek pedig akkor
nyer, ha a határon több −13 áll, mint +13. Azok a határélek, amelyekhez +13-ot írtunk, András sdzámára ,,jók''; azok
pedig, amelyekhez −13-ot írtunk, Bendek számára ,,jók''.
Módosítsuk most a számozást a következőképpen.

Ekkor is igaz, hogy a pozitív körüljárás szerinti piros-kék-zöld háromszögekben a számok összege 1, a negatív körüljárás szerint piros-kék-zöld háromszögekben -1, az összes többi háromszögekben 0, és az összes szám összege megegyezik a nagy háromszög kerületén levő számok összegével. Ez a számozás azt mutatja, hogy András akkor nyer, ha a kerületen a pozitív körüljárás szerint piros-kék élek száma nagyobb, mint a negatív körüljárás szerint piros-kék élek száma. Azok az élek, amelyeknel legalább egy csúcsa zöld, nem számítanak.
Most mutatunk egy stratégiát, amellyel bármelyik játékos megakadályozhatja, hogy az ellenfél létrehozzon egy neki megfelelő irányban piros-kék határszakaszt. A stratégia során, ameddig csak lehet, határpontokat színezünk zöldre. Ha már minden határpont ki van színezve, akkor a végeredmény már eldőlt, tetszés szerint színezhetünk ki egy belső pontot.
Egy piros, illetve kék határpontot legfeljebb egyféleképpen lehet kiegészíteni olyan piros-kék éllé, amely ellenfelünknek kedvez. Ezért, ha ellenfelünk kiszínez egy határpontot, a következő lépésben a megfelelő szomszédját zöldre színezzük, ezzel elhárítjuk a fenyegetést. Egyéb esetekben tetszés szerint zöldre színezünk egy határpontot.
Ez a stratégia minden esetben megakadályozza, hogy az ellenfél neki kedvező piros-kék határélt hozzon létre. Ezért a játékban egyik játékosnak sincs nyerő stratégiája, bármelyikük el tudja érni a (legalább) döntetlent.
Több dolgozat alapján
A. 262. 0<a<b<c egész számok. Bizonyítsuk be, hogy léteznek olyan x, y, z egész számok, amelyek nem mind 0-k, ax+by+cz=0 és |x|, |y|, |z| mindegyike kisebb, mint 2√3√c.
2000. évi Schweitzer-feladat alapján
Megoldás. Tekintsük azokat a pontokat a síkon, amelyek koordinátáira
|x|<1√3√c, |y|<1√3√c és 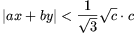
egyszerre teljesül. Jelöljük ezt a halmazt H-val.

A H halmaz a+b<c esetén egy konvex hatszög, a+bgec esetén egy négyzet belseje. A területe minden esetben nagyobb, mint c.
Blichfeldt tétele (Lásd pl. Reimann István: Geometria és határterületei, 281. oldal) alapján létezik H-nak egy olyan eltoltja, amely legalább c+1 rácspontot tartalmaz. Legyen az eltolás vektora (u,v), a rácspontok (x0,y0), ..., (xc,yc).
Tekintsük az ax0+by0, ..., axc+byc számokat. Ezek között van kettő, amelyik c-vel osztva ugyanannyi maradékot ad; az általánosság csorbítása nélkül feltehetjük, hogy ez a két szám ax0+by0 és ax1+by1. Legyen x=x0-x1, y=y0-y1 és z=-(ax+by)/c=((ax0+by0)-(ax1+by1))/c. Ezek a számok egészek, teljesül rájuk az ax+by+cz=0 egyenlet és a kívánt egyenlőtlenségek:
|x|=|(x0−u)−(x1−u)|≤|x0−u|+|x1−u|<2√3√c,
|y|=|(y0−v)−(y1−v)|≤|y0−v|+|y1−v|<2√3√c,
|z|=|(a(x0−u)+b(y0−v))−(a(x1−u)+b(y1−v))c|≤
≤|a(x0−u)+b(y0−v)|+|a(x1−u)+b(y1−v)|c<2√3√c.
Harangi Viktor és Kovács Erika Renáta megoldása alapján

