A 2001. márciusi B-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3442. Van-e olyan 2001 jegyű természetes szám, amely - a tízes számrendszerben felírva - megegyezik a 2001-edik hatványának utolsó 2001 számjegyével? (4 pont)

Javasolta: Kiss Tamás, Budapest

Megoldás. Ha egy a szám négyzete ,,a-ra végződik'', akkor minden további hatványa is; elegendő tehát olyan 2001 jegyű a számot találni, amelyre 10²⁰⁰¹|a²-a=a(a-1). Utóbbi biztosan teljesül, ha 2²⁰⁰¹|a és 5²⁰⁰¹|a-1, és akkor is, ha 5²⁰⁰¹|a és 2²⁰⁰¹|a-1. Az első két oszthatósági feltételt kielégítő számot keressük a=2²⁰⁰¹x alakban (ekkor az első oszthatóság már biztosított), erre még 2²⁰⁰¹x-1=5²⁰⁰¹y-nak, azaz 2²⁰⁰¹x-5²⁰⁰¹y=1-nek kell teljesülnie. Mivel 2²⁰⁰¹ relatív prím 5²⁰⁰¹-hez, ilyen x (és y) egész biztosan létezik, és az ezzel képezett 2²⁰⁰¹x szám 10²⁰⁰¹-nel való a₁ osztási maradéka egy, a feladat feltételét kielégítő legfeljebb 2001 jegyű szám. Hasonlóan kaphatunk olyan, ugyancsak legfeljebb 2001 jegyű a₂ számot, amelyre 5²⁰⁰¹|a₂ és 2²⁰⁰¹|a₂-1. Mivel 2²⁰⁰¹|a₁, 5²⁰⁰¹|a₂, 5²⁰⁰¹|a₁-1, 2²⁰⁰¹|a₂-1, azért a₁a₂=10²⁰⁰¹c és (a₁-1)(a₂-1)=10²⁰⁰¹d, alkalmas c>d pozitív egészekkel. Így a₁+a₂-1=a₁a₂-(a₁-1)(a₂-1)=10²⁰⁰¹(c-d) is osztható 10²⁰⁰¹-nel, ezért legalább 10²⁰⁰¹. Tehát az a₁ és a₂ közül legalább az egyik 2001 jegyű, ellenkező esetben ugyanis \(\displaystyle 10^{2001}\leq a_1+a_2-1

B.3443. Az ABCD téglalap CB oldalának B-n túli meghosszabbítására, valamint a CD oldalának D-n túli meghosszabbítására egyenlő hosszúságú szakaszokat mértünk fel. Így kaptuk az F, illetve az E pontokat. Igazoljuk, hogy az EB és az FD egyenesek metszéspontját A-val összekötő egyenes felezi az A csúcsnál lévő szöget. (3 pont)

Megoldás.

\(\displaystyle OB_1E\triangle\sim BA_1O\triangle\), így \(\displaystyle {b\over{x+c}}={d\over a}\), amiből ab=d(x+c). \(\displaystyle FA_1O\triangle\sim OB_1D\triangle\), így \(\displaystyle {b\over c}={{d+x}\over a}\), amiből ab=(d+x)c. Ebből következik, hogy d(x+c)=(d+x)c, tehát dx=cx, és mivel \(\displaystyle x\neq0\), ezért c=d. Így az AD₁OC₁ négyszög négyzet, így átlója, OA, felezi az A csúcsnál levő szöget.

B.3444. A pozitív egész számokból álló végtelen a₁, a₂, a₃, ... a_n, ... sorozatban jelölje f_n az n természetes szám előfordulásainak a számát, ha ez az érték véges.

Az a₁, a₂, ... a_n, ... sorozat ,,gyakoriságsorozata'' ezután az f₁, f₂, ... f_n, ... sorozat, ha minden f_i véges. Hasonlóan értelmezzük a fenti f₁, f₂, ... f_n, ... sorozat gyakoriságsorozataként az a₁, a₂, ... a_n, ... sorozat másodrendű gyakoriságsorozatát, ha minden gyakoriság véges, és ennek gyakoriságsorozataként a harmadrendű gyakoriságsorozatot és így tovább.

Van-e olyan a₁, a₂, ... a_n, ... sorozat, amelynek minden k-ra létezik a k-adrendű gyakoriságsorozata? (4 pont)

Megoldás. Igen, van ilyen sorozat. Az alábbi, ,,Öndokumentáló'' sorozat önmaga gyakoriságsorozata is egyben és így persze minden k-ra létezik k-adrendű gyakoriságsorozata: önmaga.

Legyen a₁=1, a₂=2=a₃. Ezután a₃ értéke szerint írjunk 2 darab 3-ast, így a₄=3, tehát most 3 darab 4-est kell írnunk, és így tovább. Szemléletesen világos, hogyan épül fel a sorozat és hogy a konstrukció akadály nélkül folytatható, az alábbiakban ennek precíz bizonyítását adjuk. Ehhez az a_n sorozattal együtt egy m_k sorozatot is definiálunk: ezek azok a helyek, ahol az a_n sorozat ,,ugrik'', m_k értéke az a legkisebb sorszám, ahol az a_n sorozat értéke k.

Legyen m₁=a₁=1. Legyen most n>1 és tegyük fel, hogy az m_k sorozat értékeit már definiáltuk, ha \(\displaystyle 1\leq ka_i sorozat elemeit is megadtuk, ha \(\displaystyle i\leq m_{n-1}\).

Az indukciós feltevés szerint \(\displaystyle n-1\leq m_{n-1}\) és így a_n-1 értéke is definiált. Legyen most m_n=m_n-1+a_n-1, a_i=n-1, ha m_n-1<i<m_n, végül legyen a_mn=n. Mivel az indukciós feltevés szerint \(\displaystyle n-1\leq m_{n-1}\) másrészt nyilván \(\displaystyle 1\leq a_{n-1}\), azért \(\displaystyle n\leq m_n\) továbbra is fennáll.

Végül a sorozat készítése alapján nyilvánvaló, hogy ha \(\displaystyle n\geq1\), akkor az n érték pontosan m_n+1-m_n=a_n-szer fordul elő a sorozatban, tehát f_n=a_n minden n-re.

B.3445. Van-e olyan háromszög, amelyet valamelyik oldalával párhuzamosan ketté lehet vágni úgy, hogy a két rész kerülete is és területe is egyenlő? (4 pont)

Javasolta: Reményi Gusztáv, Budapest

Megoldás. Bármely háromszög felosztható az egyik oldalával párhuzamos egyenessel két egyenlő területű részre: mivel az így kapott kis háromszög és a hozzá hasonló nagy háromszög területének aránya 1:2, oldalaik aránya 1:\(\displaystyle \sqrt2\). Ahhoz, hogy az a, b, c oldalú háromszög szétvágásakor a kerületek is egyenlőek legyenek, annak kell teljesülnie, hogy

\(\displaystyle {1\over{\sqrt2}}a+{1\over{\sqrt2}}b+{1\over{\sqrt2}}c={1\over{\sqrt2}}b+\left(1-{1\over{\sqrt2}}\right)a+b+\left(1-{1\over{\sqrt2}}\right)c,\)

ahonnan \(\displaystyle (\sqrt2-1)(a+c)=b\). Olyan háromszög, amelynek oldalaira ez az egyenlőség teljesül, végtelen sok van, például a=1, b=1, \(\displaystyle c=\sqrt2\) esetén az egyenlő szárú egység befogójú derékszögű háromszög.

B.3446. Határozzuk meg a q(x) polinomot úgy, hogy a p(x)=x²+x+1 polinommal p²(x)-2p(x)q(x)+q²(x)-4p(x)+3q(x)+30 azonosság teljesüljön. (4 pont)

Megoldás. Ilyen a \(\displaystyle q_1=x^2+2x-\frac{1}{2}\) és a \(\displaystyle q_2=x^2-\frac{3}{2}\) polinom. Ezeket a q-ra nézve másodfokú q²-(2p-3)q+(p²-4p+3)\(\displaystyle equiv\)0 egyenlet megoldásaiként kaphatjuk meg. Ha végiggondoljuk a másodfokú egyenlet megoldóképletének a levezetését és figyelembe vesszük azt a tényt, hogy nemnulla polinomok szorzata sosem a nullapolinom, akkor könnyen beláthatjuk, hogy az említett két polinomon túl nincs a feladatnak több megoldása.

B.3448. Mutassuk meg, hogy adott ellipszisbe írt olyan háromszögek területe, amelyek súlypontja egybeesik az ellipszis középpontjával, állandó. (4 pont)

Javasolta: Kiss Sándor, Szatmárnémeti

I. Megoldás.

Legyen az ellipszis egyenlete ax²+by²=1 (a,b>0). A háromszög csúcsainak koordinátáit jelölje (x₁,y₁), (x₂,y₂), (x₃,y₃). A súlypontra vonatkozó feltétel x₁+x₂+x₃=y₁+y₂+y₃=0 alakban írható fel. A háromszög területének kétszerese 2T=|x₂y₃-y₂x₃+x₃y₁-y₃x₁+x₁y₂-y₁x₂|=3^.|x₁y₂-x₂y₁| az x₃=-x₁-x₂, y₃=-x₁-x₂ feltétel miatt. Ezért \(\displaystyle \left({{2T}\over3}\right)^2=x_1^2y_2^2+x_2^2y_1^2-2x_1x_2y_1y_2\). Az ax₁²+by₁²=ax₂²+by₂²=a(x₁+x₂)²+b(y₁+y₂)²=1 feltételekből 2ax₁x₂+2by₁y₂=-1 is adódik, ezt a fenti képletbe kétféleképpen behelyettesítve \(\displaystyle a\left({{2T}\over3}\right)^2=y_2^2(1-by_1^2)+y_1^2(1-by_2^2)-y_1y_2(-1-2by_1y_2)=y_1^2+y_2^2+y_1y_2={1\over2}(y_1^2+y_2^2+y_3^2)\) és \(\displaystyle b\left({{2T}\over3}\right)^2={1\over2}(x_1^2+x_2^2+x_3^2)\) adódik. Az elsőt b-vel, a másodikat a-val szorozva \(\displaystyle 2ab\left({{2T}\over3}\right)^2={1\over2}(ax_1^2+by_1^2+ax_2^2+by_2^2+ax_3^2+by_3^2)=3/2,\) vagyis \(\displaystyle T={{3\sqrt3}\over{4\sqrt{ab}}}\) csak az ellipszistől függő állandó.

II. Megoldás.

Jelölje az ellipszis kis- és nagytengelyének hosszát 2A, illetve 2B, ekkor az ellipszis előáll egy A sugarú körhengernek az alapkör síkjával $ szöget bezáró síkkal való metszeteként. Vetítsük a háromszöget az alapkör síkjára. A vetület súlypontja éppen az alapkör középpontja, ez egyszerű vektoros megfontolásból látszik ha az alapkör középpontjából a csúcsokba mutatóvekktorokat felbontjuk az alapkör síkjával párhuzamos ill. arra merőleges összetevőkre, hiszen az ellipszis középpontjának merőleges vetülete éppen az alapkör középpontja. Ezért a vetület minden esetben az alapkörbe írt szabályos háromszög, hiszen minden súlyvonala egybeesik a megfelelő oldalfelező merőlegessel, és ennek következtében bármely két oldal egyenlő hosszúságú. A vetület területe tehát független az eredeti háromszögtől, csak magától az ellipszistől függ. Másrészt azonban a vetület terület éppen az eredeti háromszög területének \(\displaystyle \cos\varphi={A\over B}\)-szerese, ami könnyen igazolható ha a háromszöget és vetületét is felbontjuk egy-egy az ellipszis és az alapkör síkjának metszésvonalával párhuzamos egyenessel két-két kisebb háromszögre, melyek alapja megegyezik, és a vetület háromszögek magassága pedig a megfelelő háromszögek magasságának éppen cos\(\displaystyle varphi\)-szerese. Ezért az eredeti háromszög területe is állandó, mégpedig \(\displaystyle {{3\sqrt3}\over4}AB\)-vel egyenlő.

B.3449. Legyen a>1 adott egész szám. Bizonyítsuk be, hogy ha az x²-ay²=-1 egyenletnek van egész megoldása, akkor végtelen sok egész megoldása van. (5 pont)

Javasolta: Fried Ervin, Budapest

Megoldás. Világos, hogy a nem lehet teljes négyzet, hiszen két olyan négyzetszám különbsége nem lehet 1, ahol legalább az egyikük 1-nél nagyobb. Így \(\displaystyle \sqrt{a}\) irracionális. Feltehető, hogy a létező (x₀,y₀) megoldásban x₀,y₀>0 (x=0 nyilván lehetetlen). Legyen \(\displaystyle \beta=x_0+\sqrt{a}y_0\); ekkor \(\displaystyle beta\)>1, és \(\displaystyle beta\) hatványai (amelyek páronként különbözők) \(\displaystyle x+\sqrt{a}y\) alakúak. Minden páratlan kitevőhöz tartoző x,y-ra x²-ay²=-1 teljesül. (További részletek találhatók az áprilisi B. 3461. feladat megoldásában. )

B.3450. Tekintsük azokat a síkokat, amelyek a T tetraéder lapsíkjaival párhuzamosak, és a T-ből általuk levágott kis tetraéderek térfogata T térfogatának 1/3 része. A T térfogatának hányadrésze marad meg, ha csúcsait levágjuk ezekkel a síkokkal? (5 pont)

Megoldás. A metszősíkok és az eredeti tetraéder lapsíkjai három típusú kis tetraédert határoznak meg, amelyek a síkok párhuzamossága miatt mind hasonlók lesznek az eredeti tetraéderhez. Hasonló testek térfogatának aránya a hasonlóság arányának a köbével egyezik meg. Legyen a³=1/3.

Az eredeti tetraéder mind a 4 csúcsánál egy-egy olyan tetraéder keletkezik, amely éleinek hossza megfelelő élei hosszának a-szorosa. mind a 6 élénél egy-egy olyan tetraéder keletkezik, amely éleinek hossza megfelelő élei hosszának (2a-1)-szerese, végül pedig mind a négy lapjánál egy-egy olyan tetraéder keletkezik, amely éleinek hossza megfelelő élei hosszának (3a-2)-szorosa (lásd az ábrát).

A megmaradó test térfogata ezek alapján (ha térfgata 1 egység):

1-4^.a³+6^.(2a-1)³-4^.(3a-2)³\(\displaystyle approx\)0,01163.

Tehát a térfogatának 1163 tízezrede marad meg.

B.3451. Oldjuk meg a következő egyenletet: . (4 pont)

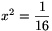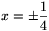Megoldás. Legyen Ekkor sin\(\displaystyle alpha\)=x és \(\displaystyle \cos\alpha=\sin({{\pi}\over2}-\alpha)=\sin\beta=\sqrt{15}x\). A trigonometrikus Pithagorasz-tételből \(\displaystyle x^2+(\sqrt{15}x)^2=1\), , adódik. Az \(\displaystyle x={1\over4}\) esetben valóban , mint ahogyan az a fenti gondolatmenet megfordításával könnyen ellenőrizhető. Hasonlóan, 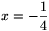esetén , ez tehát nem megoldása a feladatnak. Az egyenlet megoldása tehát \(\displaystyle x={1\over4}\).