A 2001. márciusi C-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 620. Egy trapézt szimmetrikus trapéznak nevezünk, ha alapjainak felező merőlegese egybeesik. Igaz-e, hogy ha egy trapéz szimmetrikus, akkor szimmetrikus trapéz?

Megoldás. Nem, például a paralelogramma (középpontosan) szimmetrikus, de alapjainak felező-merőlegese nem esik egybe.

C. 621. Egy sütödében, ahol mazsolás kalácsot is készítenek, a pék azt szeretné, ha a kalácsok bármely 4 dkg-os szeletében legalább 0,99 valószínűséggel lenne mazsola. 1 kg kalács elkészítéséhez hány szem mazsolát keverjen a tésztához?

Megoldás. 1 kg = 100 dkg = 25^.4 dkg, ezért ha kiválasztunk egy 4 dkg-os szeletet, akkor annak a valószínűsége, hogy egy adott mazsola nem abban a szeletben van, $\displaystyle 1-{1\over{25}}$. Ha van n darab mazsolánk, akkor annak a valószínűsége, hogy ezek egyike sem esik ebbe a szeletbe $\displaystyle \left(1-{1\over{25}}\right)^n$. A feladat feltétele szerint

$\displaystyle 1-0,99\geq\left(1-{1\over{25}}\right)^n$

$\displaystyle 0,01\geq\left({{24}\over{25}}\right)^n$

$\displaystyle n\geq112,811$

$\displaystyle n\geq113,$

tehát legalább 113 mazsolát kell 1 kg tésztába keverni.

C. 622. Adjuk meg az összes olyan 7-tel osztható 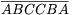$\overline{ABCCBA}$ alakú hatjegyű számot, amelyre $\displaystyle \overline{ABC}$ is 7-tel osztható. (A, B, C különböző számjegyeket jelölnek.)

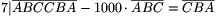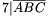Megoldás. $\displaystyle 7|\overline{ABCCBA}$, $\displaystyle 7|\overline{ABC}$ $\displaystyle Rightarrow$ $7|\overline{ABCCBA}-1000\cdot\overline{ABC}=\overline{CBA}$ . $7|\overline{ABC}$ , $\displaystyle 7|\overline{CBA}$ $\displaystyle Rightarrow$ $\displaystyle 7|\overline{ABC}-\overline{CBA}=(1000-1)A+(1-100)C=99(A-C)$. Mivel (7,99)=1, ezért ez csak úgy lehet, ha 7|A-C, azaz A-C=7 vagy A-C=-7. Öt eset van, B mindegyikben egyértelműen meghatározható abból, hogy 7|ABC.

1. eset: A=9, C=2, ekkor B=5, $\displaystyle \overline{ABCCBA}=952259$;

2. eset: A=8, C=1, ekkor B=6, $\displaystyle \overline{ABCCBA}=816618$;

3. eset: A=7, C=0, B=0 vagy 7, de ekkor nem lennének különbözők a számjegyek;

4. eset: A=2, C=9, B=5, $\displaystyle \overline{ABCCBA}=259952$;

5. eset: A=1, C=8, ekkor B=6, $\displaystyle \overline{ABCCBA}=168861$.

C. 623. Oldjuk meg a következő egyenletrendszert:

$\displaystyle \eqalign{a^2b^2-a^2-ab+1&=0\cr a^2c-ab-a-c&=0\cr abc&=-1.\cr}$

Javasolta: Kiss Sándor, Szatmárnémeti

Megoldás. A harmadik egyenletből $\displaystyle ab=-{1\over c}$. (Feltehetjük, hogy a, b, $\displaystyle c\neq0$.) Ezt az első egyenletbe helyettesítve kapjuk, hogy $\displaystyle {1\over{c^2}}-a^2+{1\over c}+1=0$ $\displaystyle \Leftrightarrow$ $\displaystyle a^2={{1+c+c^2}\over{c^2}}$ vagy $\displaystyle a=\pm{{\sqrt{1+c+c^2}}\over{|c|}}.$ Ezt a második egyenletbe behelyettesítve, majd átalakítva kapjuk, hogy $\displaystyle \pm{c\over{|c|}}\sqrt{1+c+c^2}=c+2$, amiből négyzetreemelés majd átrendezés után c=-1. Így a=$\displaystyle pm$1, és így az egyenletrendszer megoldásai

1. a=1, b=1, c=-1; ez az eredeti egyenletrendszert nem elégíti ki;

2. a=-1, b=-1, c=-1; ez viszont igen, így ez az egyetlen megoldás.

C. 624. Belefér-e százezer darab 4 cm átmérőjű szabványos pingponglabda egy 200x164x146 cm méretű ládába?

Megoldás. Nézzük meg, hogy hány labdát tudunk elhelyezni olyan módon, hogy a labdák középpontjai szabályos tetraéderrácsot alkotnak. Helyezzük el a ládát úgy, hogy a 200x164-es lapja legyen alul. Ekkor az első rétegbe (200:4)^.(164:4)=50^.41=2050 darab labda helyezhető el. A következő rétegbe csak (50-1)^.(41-1)=49^.40=1960 darab labda fér el, a következőbe ismét 2050 és így tovább. Ezek a rétegek egybe lógnak, ki kell tehát számolni egy réteg magasságát. Ezt egy olyan tetraéder segítségével tesszük meg, aminek a csúcsai megegyeznek öt pingponglabda középpontjával:

$\displaystyle x=4\sqrt2$, majd a Pitagorasz-tételből $\displaystyle m=\sqrt8$. Tehát az első réteg után minden réteg magassága $\displaystyle \sqrt8$. Mivel $\displaystyle (146-4)/\sqrt8=50,2$, ezért ezzel a módszerrel összesen 2050+25^.2050+25^.1960=102300 darab labdát tudunk elhelyezni a ládában, ami több, mint 100000. Tehát a kérdésre igennel felelhetünk.

Már regisztráltál?
Új vendég vagy?