A fizika elméleti feladatok megoldása, 2001. március

A 2001. márciusi számban kitűzött fizika elméleti feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3416. A Föld mely részén és hogyan tölthető el két vasárnap egy szombat és a rákövetkező hétfő között? (3 pont)

Takács Gábor, Budapest

Megoldás. A vasárnap-hétfő vonal közvetlen közelében. Amikor ezen a vonalon éjfél van, az egész Földön ugyanolyan nap van, de tőle keletre éppen kezdődik (0 óra), míg nyugatra éppen befejeződik (24 óra). Ha tehát a vasárnap-hétfő vonalnál szombatról vasárnapra virradólag a vonaltól nyugatra tartózkodunk, de a következő éjfélkor a befejeződő vasárnapból átlépünk a vonal keleti oldalán kezdődő vasárnapba, egymás után két vasárnapot is eltölthetünk.

P. 3417. Nagyméretű digitális órát készítettünk, ami az órát és a percet mutatja. A percek jelzéséhez 14 db fénycsövet használtunk fel, amelyek mindegyike átlagosan 2160 üzemóra után kiég. Az órát 2001. január elsején 00 óra 00 perckor indítottuk. A percet jelző fénycsövek közül várhatóan melyik és mikor ég ki elsőként, illetve várhatóan melyik és mikor ég ki utolsóként? (3 pont)

Közli: Sári Péter, Budapest

Megoldás. A 10 perceket jelző helyen a 0,1,2,... 5 számjegyek óránként 10 percet, a percek helyén a 0,1,2,... 9 számjegyek pedig óránként összesen 6 percet vilagítanak. Ebből megállapítható, hogy a legtöbbet (óranként 9x6 percet) a perceket jelző helyen a jobb alsó függőleges cső működik, míg a legkevesebbet (óranként 2x10 percet) a 10 perceket jelző helyen a bal alsó függőleges cső világít. Az első esetben 2400 óra alatt telik ki a várható élettartam, ez 100 nap, ami április 10-én éjfélkor jár le.

Hasonlóan, a legkevesebbet működő cső várható élettartama 270 nap alatt telik el, azaz szeptember 27-én éjfélkor (pontosabban 30 perccel hamarabb, mert a kérdéses cső utoljára a 23. óra 30. percében világít, amikoris 23:29-et mutat az óra -, de nem érdemes ilyen pontosan számolni, mert a várható élettartam csak egy átlagos érték).

Megjegyzés: A fénycsöveket és hasonló eszközöket nagymértékben öregítik a ki-be kapcsolások. Ezt a tényt a figyelembe véve is a korábbi megfontolással kapott fénycső ég ki a leghamarabb (legkésőbb), hisz azt kapcsolják ki-be a legtöbbször (legkevesebbszer).

P. 3418. Két egyenlő sugarú, 30 $\displaystyle Omega$ ellenállású, rézből készült körvezetőt úgy forrasztunk ösze, hogy egymás középpontjain átmennek. A forrasztási pontokra 12 V-os akkumulátort kapcsolunk.

a) Mekkora az egyik kisebb íven átfolyó áram erőssége?

b) Mekkora az akkumulátor által leadott teljesítmény? (3 pont)

Közli: Farkas László (Newton-Kupa feladat), Keszthely

Megoldás. a) 1,2 A; b) 43,2 W.

P. 3419. Egy vadász a feje felett 100 méter magasban eltalál egy húzó vadlibát, amely a vadásztól 60 méterre esik a földre. Körülbelül hány méterrel és hány fokkal kellett a madár elé céloznia, ha a lövedék sebessége 400 m/s volt? (4 pont)

Közli: Szabó Gergő, Heves, Eötvös J. Gimn.

Megoldás. A leesés ideje $\displaystyle t=\sqrt{2h/g}=4,5$ s. Az s=60 m vízszintes útból a liba sebessége v=s/t=13,4 m/s. A lövedek $\displaystyle tau$=0,25 s alatt ér fel h=100 m magasra, ennyi idő alatt a liba $\displaystyle Delta$s=v$\displaystyle tau$=3,35 m-t tett meg, tehát ennyivel kellett eléje célozni. Ez 0,0335 radiannak, azaz 1,9^o-nak felel meg.

Megjegyzés: A számítás során a lövedék mozgását egyenletesnek tekintettük, nem vettük figyelembe a sebességének (1 százaléknál is kisebb) változását. Ebben a közelítésben a puska ,,előre tartási szöge'' független a magasságtól, csak a vadliba és a lövedék sebességének arányától függ. Csillagászatban az ehhez hasonló jelenséget (a távcső ,,célzási irányának'' a Föld mozgása miatt szükséges módosítását) aberrációnak nevezik.

P. 3420. Egy hosszú, egyenes vonalzó fekszik a vízszintes asztalon. A vonalzót az egyik végéhez kötött fonal segítségével vízszintesen húzzuk. Ha a fonal a vonalzó hossztengelyével párhuzamos, akkor F₀ erő szükséges a test megmozdításához. Mekkora erővel lehet a vonalzót megmozdítani, ha a fonal merőleges a hossztengelyre? (A vonalzó egyenletesen nyomja az asztalt.) (4 pont)

Közli: Brájer László, Budapest

Megoldás. A megcsúszáskor a rúdra merőleges F erő hatására a rúd egy, a húzott végétől x távolságra eső pontja körül (éppen 0 szöggyorsulással) elfordul. Az erők és a forgatónyomatékok egyensúlyából

$\displaystyle F+{mg\mu\over l}(l-x)={mg\mu\over l}x$

és

$\displaystyle Fx={mg\mu\over2l}x^2+{mg\mu\over2l}(l-x)^2\,.$

Innen

$\displaystyle x=l/\sqrt{2}\,,\quad{\rm\acute es}\quad F=F_0(\sqrt{2}-1)\approx0{,}41F_0,$

(ahol kihasználtuk, hogy mg$\displaystyle mu$=F₀).

P. 3421. Alaszkai aranyásók népes csoportja egy széles folyóhoz érkezik. A túlsó parton - éppen szemben - egy hatalmas aranyrögöt pillantanak meg. Amelyikük először odaér, az kapja meg a bányaművelés jogát. Milyen útvonalat válasszon Joe, ha ugyanolyan gyorsan tud evezni a vizen, mint gyalogolni a szárazföldön. Számítsuk ki és rajzoljuk le Joe legkedvezőbb útvonalát, ha sebességének és a folyó sebességének aránya az aranymetszés arányszámánál a) nagyobb, b) kisebb. (Az optimális útvonal meghatározásánál grafikus módszert is használhatunk.) (5 pont)

Szokoly Gyula feladata nyomán

Megoldás. Legyen a folyó szélessége D, a víz sebessége v, és jelölje w azt a sebességet, amivel Joe futni, illetve evezni tud. Tegyük fel, hogy Joe először átevez a folyón, majd a partot érés helyétől felszalad az aranyröghöz. Ha csónakja vízhez viszonyított sebessége a vízével $\displaystyle pi$/2+$\displaystyle alpha$ szöget zár be, a folyóra merőlegesen wcos$\displaystyle alpha$ sebességgel halad, miközben v-wsin$\displaystyle alpha$ sebességgel csurog lefelé. Ennek megfelelően t₁=D/(wcos$\displaystyle alpha$) idő alatt ér át, és s=(v-wsin$\displaystyle alpha$)t₁ távolsággal az aranyrög alatt ér partot. Ezt az utat t₂=s/w=D(v-wsin alpha )/(w²cos alpha ) idő alatt teszi meg. Így az aranyrög elérése az $\displaystyle alpha$ szög függvényében

$\displaystyle t(\alpha)=t_1+t_2={D\over w}\cdot{v/w+1-\sin\alpha\over\cos\alpha}$

időt vesz igénybe. Ha $\displaystyle alpha$-t egy kicsi $\displaystyle Delta$ alpha értékkel megváltoztatjuk t($\displaystyle alpha$)

$\displaystyle t(\alpha+\Delta\alpha)={D\over w}\cdot{v/w+1-\sin\alpha\over\cos\alpha}+{D\over w}\cdot{(v/w+1)\sin\alpha-1\over\cos^2\alpha}\Delta\alpha$

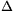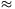
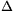
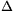
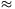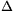
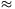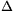
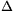
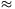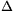
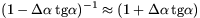értékre változik. Ennek levezetésekor kihasználtuk, hogy kis Delta $\displaystyle alpha$ esetén sin$\displaystyle Delta$ alpha approx Delta alpha , cos Delta alpha approx 1, [így sin( alpha + Delta alpha ) approx sin alpha + Delta alpha cos alpha , cos( alpha + Delta alpha ) approx cos alpha - Delta alpha sin alpha ], és azt, hogy $(1-\Delta\alpha\,{\rm tg}\alpha)^{-1}\approx(1+\Delta\alpha\,{\rm tg}\alpha)$ , a ( 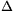Delta alpha )² nagyságú tagokat pedig elhanyagoltuk. 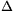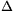(Ezek a közelítések annál jobbak, minél kisebb a Delta alpha .) Ha t( alpha ) minimális, értéke semmilyen Delta alpha mellett sem csökkenhet, ilyenkor tehát a 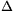Delta alpha együtthatója nulla, azaz

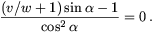
${(v/w+1)\sin\alpha-1\over\cos^2\alpha}=0\,.$

Innen

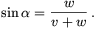
$\sin\alpha={w\over v+w}\,.$

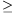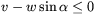Számításunk csak akkor helyes, ha v-wsin alpha 0, különben t₂ negatívnak adódik, ami annak felelne meg, hogy s<0, azaz Joe az aranyrög fölött érne partot. Ilyenkor $t_2=-s/w\,$ -vel kellene számolnunk, de ezt az esetet nem érdemes végigszámolni, mert nyilván időveszteség az aranyrög fölé evezni. Ekkor, tehát ha a $v-w\sin\alpha\leq0\,$ -nak adódik, Joenak úgy kell eveznie, hogy az eredő sebesságe merőleges legyen a folyóra. A két esetet elválasztó sebességnél

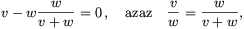
$v-w{w\over v+w}=0\,,\quad{\rm azaz}\quad{v\over w}={w\over v+w},$

ahonnan

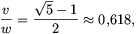
${v\over w}={\sqrt{5}-1\over2}\approx0{,}618,$

ami éppen az aranymetszés nevezetes arányszáma.

A fenti eredmény a differenciálszámítás formális szabályainak alkalmazásával, vagy az

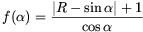
$f(\alpha)={\vert R-\sin\alpha\vert+1\over\cos\alpha}$

függvény (R=v/w) grafikus vizsgálatával is megkapható.

P. 3422. Kilenc ponttöltést helyezünk el egy 1 cm rácsállandójú, 3x3-as négyzetrács rácspontjaiban. A töltések nagyságát úgy választjuk meg, hogy az egyes töltések helyén a többi töltésből származó potenciál 10 kV legyen. Mekkora a töltések összes kölcsönhatási energiája? (5 pont)

Közli: Bakonyi Gábor, Budapest

Megoldás.Egy töltésrendszerben a kölcsönhatási energia

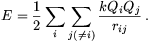
$E={1\over2}\sum_i\sum_{j(\not=i)}{kQ_iQ_j\over r_{ij}}\,.$

Jelen esetben minden töltés helyén a többi azonos U potenciált hoz létre, azaz i-től függetlenül

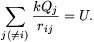
$\sum_{j(\not=i)}{kQ_j\over r_{ij}}=U.$

Ezt behelyettesítve

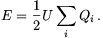
$E={1\over2}U\sum_iQ_i\,.$

A szimmetriából nyilvánvaló, hogy csak háromféle töltés van a rendszerben. Jelölje Q₁ a csúcsokon, Q₂ az élek közepén, Q₃ pedig a középpontban található töltést. Ezekre az U egyenletéből Q₁=0,052 Ua/k, Q₂=0,213 Ua/k es Q₃=0,442 Ua/k adódik, ahol a a rácsállandó.

A rendszer össztöltése: 4Q₁+4Q₂+Q₃=1,50 Ua/k=1,67^.10^-8 C, így E=7,5^.10^-5 J.

P. 3423. Az ábrán látható szabályos háromszög alakú vezető keret egyik, mozgatható oldalát egyenletesen, v=0,1 m/s sebességgel csúsztatjuk végig a másik két oldalon. A vízszintes keret függőleges irányú, homogén, B=0,4 T indukciójú mágneses mezőben van. Az oldalak hosszúsága l=1 m, ellenállásuk 1 Omega .

a) Hogyan változik időben a körben indukált elektromotoros erő?

b) Hogyan változik időben az áramerősség?

c) Mennyi munkát végzünk a csúsztatáskor, ha a súrlódás elhanyagolható? (5 pont)

Közli: Gálfi László, Budapest

Megoldás. A vezető keret területe az idő függvényében

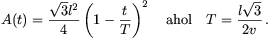
$A(t)={\sqrt{3}l^2\over4}\left(1-{t\over T}\right)^2\quad{\rm ahol}\quad T={l\sqrt{3}\over2v}\,.$

Ennek megfelelően az indukált elektromotoros erő

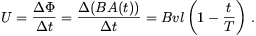
$U={\Delta\Phi\over\Delta t}={\Delta(BA(t))\over\Delta t}=Bvl\left(1-{t\over T}\right)\,.$

Mivel az ellenállás

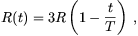
$R(t)=3R\left(1-{t\over T}\right)\,,$

az áram

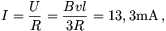
$I={U\over R}={Bvl\over3R}=13,3{\rm mA}\,,$

tehát időben nem változik. A csúsztatáshoz szükséges pillanatnyi teljesítmény P=UI, azaz

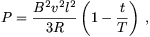
$P={B^2v^2l^2\over3R}\left(1-{t\over T}\right)\,,$

ami a teljes T időre felösszegezve

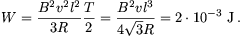
$W={B^2v^2l^2\over3R}{T\over2}={B^2vl^3\over4\sqrt{3}R}=2\cdot10^{-3}{\rm~J}\,.$

P. 3424. Egy adiabatikusan zárt rendszer két testet tartalmaz. Az A test hőkapacitása 4000 J/K és hőmérséklete 2400 K, a B test hőkapacitása 8000 J/K és hőmérséklete 300 K. Mekkora munka nyerhető ki ebből a rendszerből (mint hőerőgépből)? (6 pont)

Schwartz Lajos emlékverseny, Nagyvárad

Megoldás. Kapcsoljunk - gondolatban - a két test (mint két hőtartály) közé egy ideális hőerőgépet, és azzal végeztessünk munkát. E gépet olyan kicsi teljesítményűnek gondoljuk, hogy egy ciklusa alatt a hőtartályok hőmérséklete állandónak tekinthessük.

Egy ciklus alatt az A test által leadott, illetve B által felvett hőre igaz, hogy

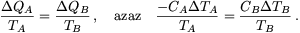
${\Delta Q_A\over T_A}={\Delta Q_B\over T_B}\,,\quad{\rm azaz}\quad{-C_A\Delta T_A\over T_A}={C_B\Delta T_B\over T_B}\,.$

Tekentellel arra, hogy jelen esetben C_B=2C_A, fennáll

2T_A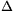T_B+T_BT_A=0,

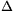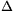ami a Delta (T_AT_B²)=0 egyenlettel egyenértékű. Ez utóbbi megoldása (T_AT_B²)=állandó (és ez az állandó a testek ismert kezdeti hőmérsékletéből számítható). Ennek megfelelően a teljes folyamat végére kialakuló közös hőmérséklet

$T_{\rm k\ddot oz\ddot os}=\root3\of{T_A^{\rm kezdeti}\left(T_B^{\rm kezdeti}\right)^2}\,.$

A rendszerből kivett (maximálisan kivehető) munka az A test által leadott és a B test által felvett hőmennyiség különbsége:

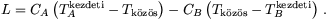
$L=C_A\left(T_A^{\rm kezdeti}-T_{\rm k\ddot oz\ddot os}\right)-C_B\left(T_{\rm k\ddot oz\ddot os}-T_B^{\rm kezdeti}\right)\,.$

Adatainkkal 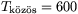$T_{\rm k\ddot oz\ddot os}=600$ K és L=4,8 MJ.

P. 3425. Milyen egy kerékpár küllős kerekének képe a célfotón? (A célfotó úgy készül, hogy a célvonal nagyon keskeny sávjáról nagyon sűrűn egymás után elektronikus kamerával felvételeket készítenek, majd ezeket egymás mellett, a kerékpár várható haladási sebességének megfelelő távolságban helyezik el.) (6 pont)

Közli: Bodor András, Budapest

célfotó

Megoldás. A felvétel folyamatát úgy is elképzelhetjük, ahogy azt a kerek tengelyehez rögzitett, de nem forgó koordinata-rendszerből látnánk: az álló tengelyű, de 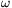omega szögsebességgel forgó kerékről egy R 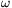sebességgel haladó keskeny, függőleges résen keresztül készítünk felvételeket egy álló fotólemezre. Tekintsük t=0-nak azt a pillanatot, amikor a tengely áthalad a célvonalon. A egész mozgás erre a pillanatra való időtükrözésre szimmetrikus, ezért a kép is szimmetrikus lesz, így elég az egyik felét nézni. A kerék abroncsa nyilván körneknek látszik, a küllők képe a kérdéses. Vegyük origónak a kerek tengelyét, mutasson az x tengely balra, az y pedig lefelé, és tekintsük azt a küllőt, amelyik a t=0-ban 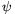$\psi$ szöget zár be a függőlegessel. A t pillanatban a küllő szöge 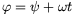$\varphi=\psi+\omega t$ , és az a pontja látszik a képen, amelyikre x=R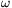t. Ekkor az 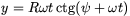$y=R\omega t\,{\rm ctg}(\psi+\omega t)$ . A küllő képe r és 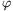phi polárkoordinátákkal kifejezve:

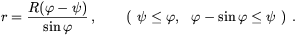
$r={R(\varphi-\psi)\over\sin\varphi}\,,\quad\quad\left(\ \psi\leq\varphi,\ \ \varphi-\sin\varphi\leq\psi\ \right)\,.$

Ez az egyenlet különböző, de rögzített 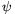$\psi$ értékeket választva sorra megadja az egyes küllők képét (lásd a vázlatos ábrát).

Már regisztráltál?
Új vendég vagy?