A 2001. áprilisi B-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B. 3452. Két játékos egy 5x5-ös táblázat mezőibe felváltva jeleket ír; a kezdő játékos mindig egy X jelet, a második pedig mindig két O jelet. Az nyer, akinek először van öt jele egy sorban vagy egy oszlopban. Milyen stratégiát kövessen a második játékos, ha nyerni akar? (4 pont)

Javasolta: Gyanta Nándor, Budapest

Megoldás. Hívjunk sorokat illetve oszlopokat üresnek, ha egyik játékos jelét sem tartalmazzák, illetve szabadnak, ha az Első játékos jelét, az X-et nem tartalmazzák. Első két jelét a Második játékos írja az első X-től és egymástól különböző üres sorba és oszlopba. Bárhogy válaszol erre az Első játékos, második lépése után a táblán marad még legalább három szabad sor és ugyanennyi szabad oszlop, ezek egyik mezőjén pedig egy O áll. Az e három szabad sor és oszlop metszéspontjaiban álló összesen 9 mezőt színezzük pirosra, a piros sorok és oszlopok további mezőit pedig kékre.

Soron következő két jelét a Második játékos írja annak a piros sornak a két szabad mezejére, ahol már van egy O. Ha most az Első játékos nem az ebben a sorban lévő valamelyik kék mezőre lép, akkor Második azonnal nyer, hiszen így ő egyetlen lépésben elfoglalhatja az ebben a sorban üresen maradt két kék mezőt.

Ezután pedig Második folyamatosan a kék területen tarthatja Elsőt, ha piros oszloponként haladva két-két O-t ír a szabad piros mezőkbe. Három ilyen lépés után már mind a kilenc piros mezon O áll és lesz egy szabad oszlop, továbbá két szabad sor, melyek mindhárom mezője piros és így, O-kal kitöltve 'háromszoros' győzelmet biztosítanak Második számára a következő lépésben. Mivel a most következő, ötödik lépésével Első sem a játékot nem tudja megnyerni, sem pedig ellenfele három darab szabad hármasának mindegyikét lezárni, bármit lépjen is, legkésőbb az ötödik lépésben Második megnyeri a játékot.

B. 3453. Legyen az ABC háromszög súlypontja S, az AS szakasz felezőpontja H, az AB oldal felezőpontja Q. Messe a H-n keresztül BC-vel húzott párhuzamos az AB oldalt P-ben, a CQ egyenest R-ben. Mekkora a PQR és az APH háromszögek területének aránya? (3 pont)

Javasolta: Káspári Tamás, Paks

Megoldás.

A párhuzamos szelők tétele szerint P harmadolja az AB szakaszt és PH=BC/6. Ezért az APH háromszög területe az ABC háromszög területének 1/3^.1/6=1/18-ad része.

A PQR és a BQC háromszögek hasonlóak, mert megfelelő oldalaik párhuzamosak. A hasonlóság aránya megegyezik a PQ:QB aránnyal, vagyis 1:3. Ezért a PQR háromszög területe a QBC háromszög területének 1/9-edrésze. A QBC háromszög területe viszont fele az ABC háromszög területének, tehát a PQR háromszög területe is az ABC területének 1/18-adrésze.

Vagyis az APH és a PQR háromszögek területe egyenlő.

B. 3454. Van 27 darab 1 cm élű kockánk.

a) Ki lehet-e festeni ezek lapjait lilára, fehérre és sárgára úgy, hogy a készletből lila, fehér, valamint sárga felszínű 3x3x3-as kockát is össze lehessen állítani?

b) Legalább hány lapot kell lilára festenünk ahhoz, hogy biztosan összerakható legyen az egységkockákból egy lila felszínű 3 cm élű kocka? (4 pont)

Megoldás. a) A 3x3-as kocka felszíne 54cm², ezért mindhárom színnel pontosan 54 lapot kell befestenünk. Osszuk a 27 kis kockát három csoportba. Az elsőbe tartozó 3 kocka mindegyikét két színnel fessük úgy, hogy 3-3 egy csúcsban találkozó lap azonos színű legyen, és mindhárom szín 2-2 kockán szerepeljen. A második csoportba tartozó 3x6 kis kocka közül az első 6 három egy csúcsban találkozó lapját fessük lilára, további két lapját fehérre, a hatodikat pedig sárgára. A második, illetve a harmadik hatos csoportnál permutáljuk a színeket úgy, hogy végül minden színből ugyanannyi lap legyen a második csoportba tartozó kis kockákon. Végül a harmadik csoportba tartozó 6 kis kocka mindegyikén két-két szomszédos lapot fessünk lilára is, sárgára is és fehérre is.

Ha lila nagy kockát akarunk összerakni, akkor az első és a második csoportból válasszuk ki azt az összesen 8 kis kockát, melyeknek 3-3 lila lapjuk van. Ezek lesznek a nagy kocka csúcsaiban. A második csoport 6 olyan kockája melyeknek két lila lapjuk van, valamint a harmadik csoport 6 kockája együtt a nagy kocka 12 élének közepére kerül, a második csoport 6 olyan kockája, melyeknek egy lila lapjuk van, a nagy kocka lapjainak közepére kerül, végül az első csoport maradék kockája - amelyiknek nincs lila lapja -, a nagy kocka közepére.

A többi színből is ugyanígy állíthatunk össze nagy kockát, hiszen a színezésnél a színek szerepe felcserélhető.

b) Ha két kis kocka összesen 12 lapját fehérre festjük, akkor biztosan nem tudunk lila nagy kockát összerakni, mert a nagy kockában csak egy olyan kis kocka van - a középső -, amelynek egyetlen lapja sem látható. Ezért 150 lap lilára festése nem elég. Ha viszont 151 lapot festünk lilára, akkor nyilván összerakható egy nagy kocka.

B. 3455. Adjunk meg végtelen sok (m, n) számpárt úgy, hogy az m, n különböző egész számoknak ugyanazok legyenek a prímosztói, és az m+1, n+1 számoknak is ugyanazok legyenek a prímosztói. (5 pont)

Javasolta: Gyanta Nándor, Budapest

Megoldás. Keressük az m és n számokat N-1 és N²-1 alakban, ekkor m+1=N és n+1=N² prímosztói nyilván megegyeznek. Ahhoz, hogy n=N²-1=(N-1)(N+1)=m(N+1)

minden prímosztója m-nek is prímosztója legyen szükséges és elegendő az, hogy N+1 kettőhatvány legyen. Végtelen sok megfelelő (m,n) számpárt kapunk tehát (2^k-2,2^2k-2^k+1) alakban, ahol k tetszőleges 1-nél nagyobb egész szám.

B. 3456. Egy tetraéder éleire pozitív egész számokat írunk. Egy lépésben a következő módon változtathatjuk meg az élekre írt számokat. Kiválasztunk egy csúcsot, és a belőle induló három élre írt számok helyébe a következőket írjuk: egy-egy élre a kiválasztott csúcsból induló másik két élre írt számok különbségét úgy, hogy az a és b számok különbségének felírásakor szabadon választhatunk a-b és b-a közül, a harmadik élre pedig a kiválasztott csúcsból induló másik két élre írt számok összegét. Előfordulhat-e, hogy néhány lépés után minden élen 0 áll? (3 pont)

Javasolta: Mezei József, Vác

Megoldás. Nem fordulhat elő. Tegyük fel ugyanis, hogy valamelyik (mondjuk a k-adik) lépés után még nem áll minden élen 0, de a (k+1)-edik lépés után már igen. Ha a (k+1)-edik lépés során az A csúcsból induló élekre írt a, b, c számokat változtattuk meg, akkor ezek közül valamelyik 0-tók különböző volt. A (k+1)-edik lépés után azt tapasztaljuk, hogy ezek közül két pár különbsége is 0-val egyenlő, tehát a=b=c=x, a másik pár összege is 0, tehát x+x=0, x=0, ami ellentmondás. A kiindulási számoknak persze nem kell pozitív egész számoknak lenniük, csak annyit kell feltenni, hogy nem mindegyik 0.

B. 3457. Határozzuk meg azon p, q pozitív prímeket, amelyekre az x⁴+p²x+q=0 egyenletnek van többszörös gyöke. (4 pont)

Javasolta: Besenyei Ádám, Budapest

Megoldás. Jelölje az egyenlet többszörös (legalább kétszeres) gyökét -a (ami szükségképpen nempozitív). Ekkor x⁴+p²x+q=(x+a)²(x²+bx+c)=(x²+2ax+a²)(x²+bx+c)= \(\displaystyle =x^4+(2a+b)x^3+(2ab+a^2+c)x^2+a(ab+2c)x+a^2c\,.\) A megfelelő együtthatók összehasonlításából így \(\displaystyle 2a+b=0\Rightarrow b=-2a\), \(\displaystyle 2ab+a^2+c=0\Rightarrow c=3a^2\), \(\displaystyle a(ab+2c)=p^2\Rightarrow4a^3=p^2\), \(\displaystyle a^2c=q\Rightarrow3a^4=q\). A két utóbbi összefüggésből 3³p⁸=3³(p²)⁴ =3^3.4⁴a¹²=2⁸ (3a⁴)³=2⁸q³. Ez csak úgy lehet, ha p=2 és q=3. Ekkor a=1, b= -2, c=3, és valóban x⁴+4x+3=(x+1)² (x²-2x+3).

B. 3458. Adott a síkon n piros pont. Mutassuk meg, hogy elhelyezhető 2n kék pont úgy, hogy a piros pontok által meghatározott minden háromszög belsejében van legalább egy kék. (5 pont)

Megoldás. Vegyünk fel úgy egy koordinátarendszert, hogy az n pont közül semelyik kettőnek ne legyen megegyező az x koordinátája. Jelölje a pontokat az x koordinátájuk szerinti növekvő sorrendben P₁, P₂,..., P_n. P₁-en és P_n-en kívül van még legalább egy P_k pont (1<k<n), amely a pontok konvex burkának határán helyezkedik el. Húzzuk meg az összes egyenest, amely a P_i pontok közül valamely kettőt összeköt. Minden 1<i<n esetén vagyünk fel egy Q_i és R_i pontot úgy, hogy az x koordinátájuk P_i-ével megegyező legyen, az egyik P_i alatt, a másik P_i felett helyezkedjen el úgy, hogy semelyik berajzolt egyenes ne válassza el azokat P_i-től. Ez nyilván megtehető. A P_k pont esetében csak egy ilyen pontot vegyünk fel: P_k alatt vagy fölött ugyanis nem halad el berajzolt egyenes, ezen az oldalon nem kell újabb pontot felvennünk. Tekintsünk most tetszőleges P_aP_bP_c háromszöget, ahol 1\(\displaystyle le\)a<b<c\(\displaystyle le\)n. Ha a P_aP_c egyenes a P_b pont fölött halad el, akkor az R_b pont, ha a P_b alatt halad el, akkor a Q_b pont a P_aP_bP_c háromszög belsejében lesz.

Megjegyzés: Minden n\(\displaystyle le\)3 esetén mutathatunk példát arra is, amikor 2n-6 pont felvétele nem elegendő: Legyen P₁P₂P_n egy háromszög, P_n-1 a P₁P₂P_n belsejében, P_n-2 a P₁P₂ P_n-1 belsejében, és így tovább, végül P₃ a P₁P₂P₄ belsejében. Ekkor minden P₁P₂P_i háromszöget (3<i\(\displaystyle le\)n) a P₁P_i-1, P₂P_i-1, PiP_i-1 szakaszok hárok háromszögre bontanak, melyek által a P₁P₂P_n háromszöget 2n-5 háromszög uniójára bontottuk fel úgy, hogy semelyik két háromszögnek nincs közös belső pontja. Ezért ebben az esetben az összes háromszög belsejének a lefogásához legalább 2n-5 pont szükséges.

B. 3459. Egy ABCD paralelogramma A, B, C, D csúcsai köré a, b, c, d sugarú egymáson kívül elhelyezkedő köröket rajzolunk úgy, hogy a+c=b+d. Mutassuk meg, hogy a szemközti csúcsok köré rajzolt körök két-két közös külső érintője érintőnégyszöget határoz meg. (4 pont)

Megoldás.

Jelölje a paralelogramma átlóinak metszéspontját O, az O-bók a külső érintőre állított merőleges talppontját pedig rendre P, Q, R, S. Jelölje továbbá a kör középpontokból az érintőkre állított merőlegesek talppontját A₁, A₂, B₁, B₂, C₁, C₂, ill. D₁, D₂. Így DD₂, OQ, BB₂ \(\displaystyle \perp\) e₁; DD₁, OS, BB₁ \(\displaystyle \perp\) e₂; CC₂, OR, AA₂ \(\displaystyle \perp\) e₃; CC₁, OP, AA₁ \(\displaystyle \perp\) e₄. Tudjuk még, hogy AO=OC és BO = OD. Ezekből következik, hogy az AA₁C₁C, AA₂C₂C, BB₁D₁D és a BB₂D₂D négyszögek trapézok, és középvonalaik rendre OP, OR, OS ill. OQ. A középvonalak hosszát az alapok hosszával kifejezve kapjuk, hogy

így OP=OQ=OR=OS, tehát a négy érintő által meghatározott négyszögbe tudunk rajzolni egy O középpontú, \(\displaystyle {{a+c}\over2}={{b+d}\over2}\) sugarú kört, tehát a négyszög érintőnégyszög.

B. 3460. Egy háromszögben a beírt körnek a 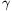szöggel szemközti oldalon lévő érintési pontja az oldalt x és y hosszú szakaszokra osztja. Bizonyítsuk be, hogy a háromszög területe \(\displaystyle xy\ctg{{\gamma}\over2}\). (4 pont)

Javasolta: Besenyei Ádám, Budapest

Megoldás. Jelöljük a háromszög oldalait a,b,c-vel, kerületét 2s-sel, beírt körének sugarát r-rel, területét pedig T-vel.

Ismert, hogy a beírt kör oldalakon lévő érintési pontjai által meghatározott x,y,z szakaszokra (lásd az ábrát) \(\displaystyle x=s-a,\;y=s-b,\;z=s-c\) teljesül. Mivel a beírt kör középpontja a szögfelezők metszéspontja, ezért az ábráról az is leolvasható, hogy \(\displaystyle \cot\frac{\gamma}{2}=(s-c)/r.\)

Tehát a bizonyítandó állítás:

Héron képlete szerint \(\displaystyle T=\sqrt{s(s-a)(s-b)(s-c)},\) ezért elegendő azt megmutatnunk, hogy

ez viszont nyilván igaz, mert ismert, hogy T=sr.

B. 3461. Legyenek a>0 és c\(\displaystyle ne\)0 adott egész számok. Bizonyítsuk be, hogy ha az x²-ay²=c egyenletnek van legalább 4c²+1 különböző egész megoldása, akkor végtelen sok egész megoldása van. (5 pont)

Javasolta: Fried Ervin, Budapest

Megoldás. Az a nem lehet négyzetszám, mivel c nem írható fel 4c²+1-féleképpen két (nemnulla) négyzetszám különbségeként. Legyen \(\displaystyle \sqrt a=\alpha\). A skatulyaelv szerint létezik két olyan megoldás, (x,y) és (u,v), amelyre c|x-u\(\displaystyle ne\)0 és c|y-v\(\displaystyle ne\)0, azaz x-u=tc, y-v=sc. Tekintsük a \(\displaystyle gamma\)=n+k\(\displaystyle alpha\) alakú számokat, ahol n és k tetszőleges egészek, és vezessük be a \(\displaystyle gamma\)^*=n-k\(\disp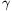laystyle alpha\), N(\(\displaystyle gamma\))=\(\displaystyle gamma\)^*=n²-ak² jelöléseket; könnyen belátható, hogy ekkor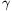 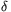N(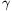)=N()N(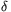) teljesül. 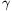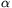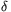Esetünkben a :=x+y, :=u+v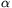 számokra c²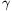=N(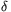)N(^*)=N(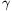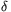^*). Itt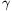 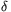^*=(x+y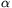)(u-v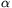)=(xu-ayv)+(yu-xv)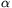= (u(u+tc)-av(v+sc))+(u (v+sc)-v(u+tc))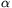=(u²-av²+ c(ut-avs))+c(us-vt)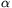=c((1+ut-avs)+(us- vt)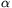). 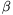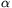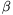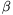A :=(1+ut-avs)+ (us-vt) jelölést bevezetve így c²=N(c)=N(c)N ()=c²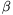N (), tehát N (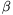)=1. 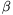Mivel 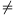1, az (x+y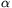)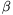^m számok (m=1,2,3,...) mind különbözők, és (x+y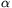) 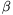^m=x _m+y_m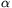 alakba írhatók, alkalmas x_m és y_m egészekkel. 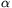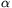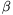Ezekre pedig N (x_m+y_m)=N(x+y )N ()^m= c^.1^m=c miatt x_m ²-ay_m²=c teljesül.