A fizika elméleti feladatok megoldása, 2001. április

A 2001. áprilisi számban kitűzött fizika elméleti feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3426. Két egymás melletti pályán közlekedő vonat egyike 90 km-t tesz meg óránként, a másik 10 métert másodpercenként. Az egyik vonatban ülő utas azt észleli, hogy a másik vonat 8 másodperc alatt halad el mellette. Mekkora a másik vonat hossza? (3 pont)

Jedlik Ányos verseny, Nyíregyháza

Megoldás. A két vonat sebessége 25 m/s, illetve 10 m/s, így a relatív sebességük 15 m/s, ha azonos, illetve 35 m/s, ha ellentétes irányba haladnak. Ennek megfelelően a másik vonat hossza vagy 8^.15=120 m, vagy 8^.35=280 m.

P. 3427. Egy utasszállító repülőgép a kifutópályáról 180 km/h sebességgel emelkedik fel, és egyenes vonalú pályán egyenletesen gyorsulva 40 másodperc alatt 2000 méter magasságra jut, miközben sebessége 540 km/h-ra növekszik.

a) Emelkedés közben mekkora és milyen irányú a repülőgép gyorsulása?

b) Emelkedéskor az utastér padlóján lévő börönd nem csúszik meg. Legalább mekkora a tapadási súrlódási együttható? (Tételezzük fel, hogy a padló síkja párhuzamos a sebességgel!) (4 pont)

Párkányi László verseny, Pécs

Megoldás. a) Az emelkedés kezdetekor a sebesség v₁=50 m/s, t=40s mulva v₂=150 m/s. Az átlagsebesség (v₁+v₂)/2=100 m/s, tehát a 40 s alatt a gép 4000 m-t tesz meg. Közben 2000 m-t emelkedik, így az emelkedés szöge $\displaystyle alpha$=30^o. Ez egyben a gyorsulás iránya is. A gyorsulás nagysága a=(v₂-v₁)/t=2,5 m/s². b)

A bőröndre ható súrlódási erő S=ma+mgsin$\displaystyle alpha$, miközben a bőröndöt N=mgcos$\displaystyle alpha$ erő nyomja a repülő padlójához. Ebből

$\displaystyle \mu\geq{g\sin\alpha+a\over g\cos\alpha}\approx0,87.$

P. 3428. Vékony, m tömegű pálca egyik végéhez merőlegesen kis tengelyt erősítettünk. A tengely az ábrán látható vízszintes sínpáron súrlódásmentesen csúszhat. Labilis egyensúlyi helyzetéből a pálca valamerre eldől.

a) Lesz-e a sínpárra ható nyonóerő valamikor nulla?

b) Elválik-e dőlés közben a pálca tengelye a síntől?

c) Mekkora a nyomóerő a 0^o-os, 90^o-os és 180^o-os elfordulás pillanatában? (5 pont)

Közli: Holics László, Budapest

Megoldás. Súrlódás hiányában a sín csak függőleges (N nagyságú)erővel hat a pálcára, ennek megfelelően a súlypont egy függőleges egyenes mentén mozog. Jelölje az $\displaystyle \ell$ hosszúságú, m tömegű és $\displaystyle \Theta=m\ell^2/12$ tehetetlenségi nyomatékú pálca súlypontja elmozdulását x, a súlypont sebességét v, gyorsulását a, a pálcának a függőlegessel bezárt szögét $\displaystyle phi$, szögsebességét $\displaystyle omega$, szöggyorsulását pedig $\displaystyle beta$! A gyorsulásra és szöggyorsulásra igaz, hogy

ma=mg-N,

$\displaystyle \Theta\beta={N\ell\over2}\sin\varphi,$

és amíg a pálca vége a síneken mozog

$\displaystyle x={\ell\over2}(1-\cos\varphi),$

$\displaystyle v={\ell\over2}\omega\sin\varphi,$

$\displaystyle a={\ell\over2}\omega^2\cos\varphi+{\ell\over2}\beta\sin\varphi.$

Az energia-megmaradás törvénye szerint

$\displaystyle mg(1-cos\varphi)={1\over2}mv^2+{1\over2}\Theta\omega^2.$

Ezekből

$\displaystyle N={3(\cos\varphi-1)^2+1\over(3\sin^2\varphi+1)^2}mg.$

a) Ez a kifejezés mindig pozitív (jóllehet $\displaystyle phi$=61^o-nál majdnem nullára, kb. 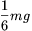${1\over6}mg$ -re csökken),

b) tehát a pálca tengelye nem válik el a síntől.

c) A nyomóerő értéke a kérdéses helyzetekben rendre mg, $\displaystyle {1\over4}mg$ és 13mg.

P. 3429. Egy pingpongozó úgy mozgatja fel-le az ütőt, hogy a labda mindig 40 cm magasra pattan fel az ütőről. Az ütközési szám 0,5. Mekkora az ütő sebessége, amikor megüti a labdát? (A labda tömege sokkal kisebb, mint az ütőé, és a légellenállás elhanyagolható.) (4 pont)

Közli: Varga István, Békéscsaba

Megoldás. Mivel a labda ugyanolyan magasra pattan vissza, mint amilyenről leesett, az ütközéskor a labda v sebességének csak az iránya változik meg, a nagysága nem. Az ütő u sebessége az ütközéskor (a nagy tömegarány miatt) nem változik, így a relatív sebesség ütközés előtt u+v, utána pedig u-v. Ezek aránya az ütközési szám:

$\displaystyle k={u-v\over u+v},$

ahonnan

$\displaystyle u={1+k\over1-k}v=3v.$

Esetünkben $\displaystyle v=\sqrt{2gh}=2{,}8$ m/s, azaz u=8,4 m/s.

P. 3430. A Pireneusokban 1969 óta működtetnek egy napkohót, melyben 63 darab 30 m²-es tükör vetíti a napfényt egy kis helyre. Legalább mennyi energiát összpontosítottak a tükrök, ha 1 perc alatt 1 cm vastag, kezdetben 35 ^oC-os vaslapba 15 cm sugarú lyukat olvasztottak a napsugarak? Legalább mekkora a napkohó teljesítménye? (3 pont)

,,Keresd a megoldást!'' verseny, Szeged

Megoldás. Ha a lemez vastagsága d=0,01 m, a lyuk sugara r=0,15 m, akkor az olvasztásra fordított energia

E_olv=(r²$\displaystyle pi$d)$\displaystyle rho$(c$\displaystyle Delta$T+c_olv).

Itt $\displaystyle rho$=7860 kg/m³ a vas sűrűsége, c=0,4648 kJ/kg ^oC a fajhője, c_olv=272,2 kJ/kg az olvadáshő, végül $\displaystyle Delta$T=1501 ^oC az olvadáspont és a kezdeti hőmérséklet különbsége, tehát E_olv=5,4 MJ. Mivel a vas a hő egy részét elvezeti, ennél több energiát kellett egy perc alatt összpontosítani, így a teljesítmény legalább 90 kW.

P. 3431. Egy kádban T₀=80 ^oC-os víz van, a környezet T^*=20 ^oC-os. A víz hőmérséklete az idő függvényében: T(t)=T^*+(T₀-T^*)e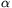^-t, ahol 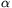alpha a hűlésre jellemző állandó. Az első 5 percben a hőmérséklet 10 ^oC-kal csökken. Ezután mennyi idő múlva töltsünk a kádba még ugyanannyi 10 ^oC-os vizet, hogy a keverék hőmérséklete a leghamarabb érje el a 30 ^oC-ot? (5 pont)

Közli: Simon Péter, Pécs

Megoldás. A hűlési képlet szerint bármely t₂>t₁-re

$\displaystyle T(t_2)=T^{\ast}+\left(T(t_1)-T^{\ast}\right)e^{-\alpha(t_2-t_1)},$

azaz

$\displaystyle T(t_1)-T(t_2)=\left(T(t_1)-T^{\ast}\right)\left(1-e^{-\alpha(t_2-t_1)}\right).$

Ebből látszik, hogy adott időtartam alatt a víz hőmérséklete annál többet csökken, minél magasabb hőmérsekletről indul a hűlése. Eszerint először hagyni kell hűlni, és akkor kell hideg vizet bekeverni, amikor azzal épp beállítjuk a kívánt véghőmérsékletet, azaz akkor, amikor a kád vize 50 ^oC-os. A

$\displaystyle T(t_1)=T^{\ast}+\left(T_0-T^{\ast}\right)e^{-\alpha t_1}$

[t₁=5 perc, T(t₁)=70 ^oC] és a

$\displaystyle T(t_2)=T^{\ast}+\left(T(t_1)-T^{\ast}\right)e^{-\alpha(t_2-t_1)}$

[T(t₂)=50 ^oC] egyenletekből

$\displaystyle t_2-t_1=t_1{\displaystyle\ln\left({\displaystyle T(t_1)-T^{\ast}\over\displaystyle T(t_2)-T^{\ast}}\right)\over\displaystyle\ln\left({\displaystyle T_0-T^{\ast}\over\displaystyle T(t_1)-T^{\ast}}\right)}.$

Eszerint az első öt perc után még t₂-t₁=14 perccel kell a hideg vizet a kádba önteni.

P. 3432. Egy szabályos tetraéder csúcsaiban egyforma fémgömbök helyezkednek el. A gömbök nem érnek össze. Egyetlen (A) gömbre vitt 20 nC töltés azt ugyanakkora potenciálra tölti fel, mintha A-nak és egy másik gömbnek adnánk 15-15 nC töltést. Mekkora egyenlő töltéseket kellene adnunk A-nak és két másiknak, és mekkorát mind a négy gömbnek, hogy az A gömb potenciálja mindig ugyanakkora legyen? (6 pont)

Közli: Bihary Zsolt, Irvine, California

Megoldás. A probléma lineáris voltából következik, hogy ha tudjuk egy bizonyos (I) töltéselrendezés esetén a gömbök potenciáljait, és egy másik (II) esetben ugyancsak ismerjük a potenciálokat, akkor a két töltéselrendezés ,,szuperpozíciójában'' mindegyik gömb potenciálja az (I) és a (II) eseteknek megfelelő potenciálok összege lesz. Az is igaz, hogy ha valamelyik töltéselrendezésben az összes töltés nagyságát $\displaystyle lambda$-szorosra növeljük, akkor a potenciálok is $\displaystyle lambda$-szorosra változnak.

A feladat szövege szerint ha Q_A=Q_B=15 nC (és a többi gömb töltetlen), akkor U_A nagysága egy bizonyos U₀, és Q_A=Q_C=15 nC esetén (a tetraéder szimmetriája miatt) U_A ugyancsak U₀. Szuperponáljuk egymásra ezt a két töltéselrendezést, és vonjuk ki belőlük azt, amikor csak az A gömbnek van 15 nC töltése. Ilyenkor Q_A=Q_B=Q_C=15 nC (a negyedik gömb töltetlen), és az A gömb potenciálja $\displaystyle U_A=U_0+U_0-{15\over20}U_0={5\over4}U_0$. Ha azt akarjuk, hogy A potenciálja éppen U₀ legyen, a töltéseket $\displaystyle {4\over5}$ arányban csökkentenünk kell, tehát Q_A=Q_B=Q_C=12 nC.

Hasonló módon kaphatjuk meg, hogy mind a négy gömböt 10 nC-ra töltve az A gömb potenciálja éppen U₀ lesz. Megjegyzés: Ha a gömbök távolsága sokkal nagyobb lenne, mint a sugaruk, akkor az elektromos terüket a pontszerű töltés közelítésében számíthatnánk. Jelen esetben (a megadott számadatokkal) ez nem is teljesül, a gömbök mérete és a távolságuk összemérhető, emiatt egymást erősen polarizálják. A töltéseloszlások és az elektromos mező csak nagyon bonyolult módon számítható ki, de szerencsére ezekre -- a fenti gondolatmenetet követve -- nincs szükség.

P. 3433. Egy régi voltmérő az 1 V-os méréshatáron 0,7 V-nak, a 10 V-os méréshatáron 2,6 V-nak méri ugyanannak a telepnek a feszültségét. Mit mutat a voltmérő 100 V-os méréshatáron? (4 pont)

Romániai feladat nyomán

Megoldás. Ezek a voltmérők egy ideális (tehát végtelen ellenállású) voltmérővel párhuzamosan kötött R_v ellenállásként képzelhetők el. A méréshatár 10-szeres (100-szoros) kiterjesztésekor a voltmérő elé 9R_v (99R_v) előtétellenállást kötünk, így az ideális műszer a 10R_v (100R_v) ellenállás tizedén (századán) eső feszültséget méri.

Ha a telep belső ellenállása R_t, feszültsége pedig U, a műszer a különböző méréshatárokon (azt is figyelembe véve, hogy a számlapot a méréshatártól függően átskálázzuk) rendre

$\displaystyle U_1=U{R_v\over R_t+R_v},$

$\displaystyle U_{10}=U{10R_v\over R_t+10R_v},$

$\displaystyle U_{100}=U{100R_v\over R_t+100R_v}$

értékeket mutat. Ezekből

$\displaystyle U_{100}={10U_{1}\over11U_{1}-U_{10}}U_{10}=3{,}6~\rm V.$

A telep feszültsége is kiszámítható: U=3,7 V.

P. 3434. Határozzuk meg az ábrán látható, csupa 1 k$\displaystyle Omega$-os ellenállásból álló végtelen hálózat eredő ellenállását az A és C, illetve az A és B pontok között! (6 pont)

Közli: Gnädig Péter, Budapest

Megoldás. A megoldás során két dolgot használunk ki:

(i) A hálózat egy öt ellenállásból álló blokk végtelen ismétléséből áll, így az első blokk leválasztása után maradó rész tulajdonságai az eredetiével azonosak.

(ii) A három pólusú hálózat három -- csillag alakba kötött --ellenálással helyettesíthető. (A helyettesítő kapcsolás lehet delta-kapcsolás is.)

Jelölje a csillagba kötött ellenállások közös pontját O-val, és legyen az R_AO=R_CO=R, illetve R_BO=r. Nyilván R_AC=2R és R_AB=R+r. Ezekre (i) szerint (minden ellenállást k$\displaystyle Omega$ egységben mérve) az

$\displaystyle {1\over R_{AC}}={1\over2R}={1\over2}+{1\over2(1+R)},$

illetve az

$\displaystyle {1\over R_{AB}}={1\over R+r}=1+{1\over\displaystyle(1+R)+{\strut1\over\displaystyle{\strut1\over\displaystyle1+r}+{\strut1\over\displaystyle2+R}}}$

egyenletek írhatók fel, melyeket megoldva

$\displaystyle R_{AC}=\sqrt{5}-1\approx1,236~{\rm k}\Omega,$

és

$\displaystyle R_{AB}={\sqrt{5}+\sqrt{21}\over4}-1\approx0,705~{\rm k}\Omega.$

P. 3435. A hálózati váltófeszültségre egy 0,2 H induktivitású és 62,8 $\displaystyle Omega$ ohmos ellenállású tekercset kapcsoltunk.

a) Mekkora kapacitású kondenzátor kapcsolható sorba a tekerccsel anélkül, hogy a hasznos teljesítmény megváltozna? Változik-e a teljesítménytényező értéke?

b) Javítható-e a teljesítménytényező azáltal, hogy a tekerccsel párhuzamosan egy kondenzátort kapcsolunk? Növelhető-e 1-re a teljesítménytényező? (4 pont)

Vermes Miklós verseny, Sopron

Megoldás. a) Az RL körbe még egy C kapacitást kötve általában mind az impedancia, mind pedig a teljesítménytényező megváltozik:

$\displaystyle Z_{RL}=\sqrt{(L\omega)^2+R^2}\quad\Longrightarrow\quad Z_{RLC}=\sqrt{(L\omega-1/C\omega)^2+R^2}$

$\displaystyle \cos\varphi_{RL}={R\over\sqrt{(L\omega)^2+R^2}}\quad\Longrightarrow\quad\cos\varphi_{RLC}={R\over\sqrt{(L\omega-1/C\omega)^2+R^2}}.$

Ha most az U²cos$\displaystyle phi$/Z hasznos teljesítmény nem változik, akkor

$\displaystyle \left(L\omega-{1\over C\omega}\right)^2=(L\omega)^2,$

azaz

$\displaystyle C={1\over2L\omega^2}=25{,}3~\mu\rm F.$

Ilyenkor mind az impedancia, mind a teljesítménytényező változatlan, csak az ellenállás induktív helyett kapacitív lesz.

b) Igen, javítható! Az RL ágban folyó I_RL=U/Z_RL áram fázisa $\displaystyle phi$_RL értékkel késik a feszültségéhez képest, míg a C ágban folyó I_C=UC$\displaystyle omega$ áramé 90^o-kal siet. Ha tehát I_C=I_RLsin$\displaystyle phi$_RL, a két áram összege fázisban van a feszültséggel, azaz a teljesítménytényező éppen 1. Ebből

$\displaystyle C={L\over(L\omega)^2+R^2}=25{,}3~\mu\rm F.$

Megjegyzés. A hasznos teljesítmény ilyenkor sem változik, csak most az RL ág áramának azt a részét, amely a meddő teljesítményt okozná, nem a hálózat, hanem a C kondenzátor szolgáltatja.

P. 3436. Nevenincs csillag egyik bolygója hosszú, henger alakú. A bolygó átlagsűrűsége ugyanakkora, mint a Földé, sugara is megegyezik a Föld sugarával, tengelyforgási ideje pedig éppen 1 nap.

a) Mekkora az első kozmikus sebesség ennél a bolygónál?

b) A bolygó felszíne felett milyen magasan keringenek az ottani távközlési szinkron-műholdak?

c) Mekkora a második kozmikus sebesség ennél a bolygónál? (5 pont)

Közli: Horányi Gábor, Budapest

Megoldás. Egy nagyon (,,végtelenül'') hosszú henger körül a gravitációs erőtér hengerszimmetrikus, és mindkét végtől távol radiális, azaz a tengelyre merőleges. A gravitációs erőtörvény és a Coulomb-törvény analógiáját felhasználva megállapíthatjuk, hogy egy m tömegből kilépő erővonalak száma (azaz a gravitációs gyorsulás és a rá merőleges felület szorzata) 4$\displaystyle pi$f^.m. Eszerint egy L magasságú, r sugarú henger palástján kilépő g-vonalak száma és a hengerben található tömeg kapcsolata:

g2r$\displaystyle pi$L=4$\displaystyle pi$fR²$\displaystyle pi$D$\displaystyle rho$,

azaz

$\displaystyle g(r)={2\pi fR^2\rho\over r}.$

A fenti erőtörvény szerint a körpályán keringés sebessége a sugártól függetlenül, így a bolygó felszínén is

$\displaystyle v=\sqrt{2fR^2\pi\rho},$

tehát a bolygón ez az első kozmikus sebesség. Ez a Földre érvényes $\displaystyle v_F=\sqrt{4R^2\pi f\rho/3}=7{,}9~\rm km/s$ értéknél $\displaystyle \sqrt{3/2}$-szer nagyobb, mintegy 9,7 km/s. b)

Az r sugarú pályán a keringési idő T_r=2$\displaystyle pi$r/v, tehát ha egy nap T₀ hosszú, a szinkronműhold pályasugara

$\displaystyle r_0={T_0v\over2\pi}=R\sqrt{T_0^2f\rho\over2\pi}.$

A Föld esetében ez a távolság $\displaystyle r_{0,F}=R{\root3\of{T_0^2f\rho/3\pi}}$, azaz

$\displaystyle r_0=\sqrt{2r_{0,F}^3\over3R}\approx1{,}33\cdot10^8~\rm m$

. A távközlési szinkronműholdak tehát r₀-R=1,27^.10⁸ m magasan keringenek a hosszú, henger alakú bolygó felszíne felett. c)

A második kozmikus sebesség, azaz a bolygóról való szökési sebesség nagyon nagy, hogy pontosan mekkora, az a bolygó hosszától függ. Végtelen hossz esetén a szökési sebesség is végtelen nagy, egy r^-1-es erőtérbol ugyanis nem lehet megszökni. Ennek belátására tekintsük a távolságoknak egy mértani haladvány szerint növekvő sorozatát: r_n=$\displaystyle alpha$ⁿr₀ ($\displaystyle alpha$>1 és mondjuk r₀=R). Az r_n-1 magasságból az r_n magasságba való feljutáshoz szükséges E(r_n-1$\displaystyle arrow$r_n) energia független az n-től: ahogy n nő, amennyire csökken az erő, annyira nő az út. Végül is az r₀ magasságból az r_N magasságba való feljutáshoz E(r₀$\displaystyle arrow$r_N)=NE(r₀$\displaystyle arrow$r₁) energia kell. Már ebből is látszik, hogy véges energiával csak véges magasságra lehet feljutni. (Ugyanez integrálszámítással is belátható.)

Ha a bolygó nem végtelen hosszú (a hossza mondjuk H), akkor amíg a végeitől távol vagyunk, és $\displaystyle r\ll H$, addig az erőtörvény 1/r-es, de ha már $\displaystyle r\simeq H$, az erőtörvény jellege megváltozik, és $\displaystyle r\gg H$ esetén a megszokott 1/r²-es lesz. Egy ilyen bolygóról már véges nagyságú kezdősebességgel indulva is meg lehet szökni, csak az $\displaystyle r\gg H$ magasságba való feljutáshoz szükséges energia ,,megdobja" a költségeket.

Integrálszámítás segítségével belátható, hogy a második kozmikus sebesség az első kozmikus sebességnek kb. $\displaystyle \sqrt{2}\cdot\ln(H/R)$-szerese. Ez a faktor még $\displaystyle H\gg R$ esetén sem túlságosan nagy (pl. H=10R-nél v_II/v_I kb. 3, és H=1000R-nél sem nagyobb 10-nél).

Már regisztráltál?
Új vendég vagy?