A 2001. májusi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 266. Az A₁, A₂, A₃, B₁, B₂, B₃ pontok egy körön helyezkednek el. Tetszőleges 0<t<1 valós számra legyen C_i(t) és D_i(t) az A_iB_i szakaszt t:(1-t) arányban osztó pont (i=1, 2, 3). Legyen e(t) a C₁(t)C₂(t)C₃(t) és D₁(t)D₂(t)D₃(t) háromszögek körülírt köreinek hatványvonala (ha létezik).

Igazoljuk, hogy az e(t) egyenesek vagy párhuzamosak, vagy egy ponton mennek át.

Dőtsch András, Szeged

Megoldás. Az állítást koorináta-geometriai eszközökkel bizonyítjuk. Vegyünk fel egy olyan derékszögű koordináta-rendszert, amelynek origója a kör középpontja, az egység pedig a kör sugara.

A későbbiekben kényelmesebb lesz t helyett az $\displaystyle u=t-{1\over2}$ paraméter használata.

Legyenek a pontok koordinátái A_i=(a_i,1,a_i,2), B_i=(b_i,1,b_i,2), C_i=(c_i,1,c_i,2), D_i=(d_i,1,d_i,2) (i=1,2,3). Az A_i és B_i pontok az origó körüli egységkörön vannak, tehát minden i-re

a_i,1²+a_i,2²=b_i,1²+b_i,2²=1.

A C_i és D_i pontok $\displaystyle \left({1\over2}+u\right):\left({1\over2}-u\right)$, illetve $\displaystyle \left({1\over2}-u\right):\left({1\over2}+u\right)$ arányban osztják az A_iB_i szakaszt, ezért

(1) $\displaystyle c_{i,j}=\left({1\over2}-u\right)a_{i,j}+\left({1\over2}+u\right)b_{i,j}$

és

(2) $\displaystyle d_{i,j}=\left({1\over2}+u\right)a_{i,j}+\left({1\over2}-u\right)b_{i,j}$

(i=1,2,3; j=1,2).

Tekintsük a C₁C₂C₃ háromszög köré írt kör egyenletét. Az egyenlet determináns alakja:

(3) $\displaystyle \left|\matrix{x^2+y^2&x&y&1\cr c_{1,1}^2+c_{1,2}^2&c_{1,1}&c_{1,2}&1\cr c_{2,1}^2+c_{2,2}^2&c_{2,1}&c_{2,2}&1\cr c_{3,1}^2+c_{3,2}^2&c_{3,1}&c_{3,2}&1\cr}\right|=0.$

Ebbe behelyettesítjük (1)-et és (2)-t. Közben figyelembe vesszük, hogy

c_i,1²+c_i,2²=

$\displaystyle =\left(\bigg({1\over2}-u\bigg)a_{i,1}+\bigg({1\over2}+u\bigg)b_{i,1}\right)^2+\left(\bigg({1\over2}-u\bigg)a_{i,2}+\bigg({1\over2}+u\bigg)b_{i,2}\right)^2=$

$\displaystyle =\left({1\over4}-u+u^2\right)(a_{i,1}^2+a_{i,2}^2)+\left({1\over4}+u+u^2\right)(b_{i,1}^2+b_{i,2}^2)+$

$\displaystyle +2\left({1\over4}-u^2\right)(a_{i,1}b_{i,1}+a_{i,2}b_{i,2})=$

$\displaystyle =2\left({1\over4}-u^2\right)(a_{i,1}b_{i,1}+a_{i,2}b_{i,2}-1)+1.$

A (3) egyenlet a behelyettesítés után a következő alakú:

(4) $\displaystyle \left|\matrix{x^2+y^2&x&y&1\cr p_1\big({1\over2}-u^2\big)+1&q_1u+r_1&s_1u+t_1&1\cr p_2\big({1\over2}-u^2\big)+1&q_2u+r_2&s_2u+t_2&1\cr p_3\big({1\over2}-u^2\big)+1&q_3u+r_3&s_3u+t_3&1\cr}\right|=0,$

ahol a p_i, q_i, r_i, s_i, t_i, u_i számok csak az A_i és B_i pontok koordinátáitól függnek, u-tól nem.

Ha az első oszlopból kivonjuk az utolsót, akkor a determináns értéke nem változik, ezért az egyenlet a következő alakban is felírható:

(5) $\displaystyle \left|\matrix{x^2+y^2-1&x&y&1\cr p_1\big({1\over2}-u^2\big)&q_1u+r_1&s_1u+t_1&1\cr p_2\big({1\over2}-u^2\big)&q_2u+r_2&s_2u+t_2&1\cr p_3\big({1\over2}-u^2\big)&q_3u+r_3&s_3u+t_3&1\cr}\right|=0.$

Ha kifejtjük a baloldalán álló determinánst, akkor a következő alakú egyenletet kapjuk:

(6) $\displaystyle P(u)(x^2+y^2-1)+\bigg({1\over4}-u^2\bigg)\big(Q(u)x+R(u)y+S(u)\big)=0,$

ahol P és S legfeljebb másodfokú polinom, Q és R pedig legfeljebb elsőfokú. A továbbiakban csupán erre az információra lesz szükségünk.

(Ugyanezt az eredményt megkaphatjuk más módszerekkel is, a kör egyenletének determináns alakja nélkül.)

A D₁D₂D₃ háromszög köré írt kör egyenletét úgy kaphatjuk meg, hogy a (6) egyenletet u helyett a -u számmal írjuk fel. A D₁D₂D₃ háromszög köré írt kör egyenlete tehát:

(7) $\displaystyle P(-u)(x^2+y^2-1)+\bigg({1\over4}-u^2\bigg)\big(Q(-u)x+R(-u)y+S(-u)\big)=0.$

A két kör hatványvonalának egyenlete a (6) és (7) egyenleteknek olyan lineáris kombinációja, amelyben a másodfokú tagok kiesnek. Ez teljesül például akkor, ha a (6) egyenletet P(-u)-val, a (7) egyenletet P(u)-val megszorozzuk, majd kivonjuk egymásból. A hatványvonal egyenlete tehát:

$\displaystyle \bigg({1\over4}-u^2\bigg)\bigg(\big(Q(u)P(-u)-Q(-u)P(u)\big)x+\big(R(u)P(-u)-R(-u)P(u)\big)y+$

+S(u)P(-u)-S(-u)P(u))=0.

A második tényezőben az együtthatók u-nak legfeljebb negyedfokú polinomjai, ráadásul a páros kitevőjű tagok mind kiesnek. Ezért

Q(u)P(-u)-Q(-u)P(u)=$\displaystyle alpha$₁u³+$\displaystyle beta$₁u,

R(u)P(-u)-R(-u)P(u)=$\displaystyle alpha$₂u³+$\displaystyle beta$₂u,

S(u)P(-u)-S(-u)P(u)=$\displaystyle alpha$₃u³+$\displaystyle beta$₃u

alkalmas $\displaystyle alpha$_i és $\displaystyle beta$_i valós számokkal. A hatványvonal egyenlete behelyettesítés és egyszerűsítés után:

($\displaystyle alpha$₁x+$\displaystyle alpha$₂y+$\displaystyle alpha$₃)u²+($\displaystyle beta$₁x+$\displaystyle beta$₂y+$\displaystyle beta$₃)=0.

Ha az $\displaystyle alpha$₁x+$\displaystyle alpha$₂y+$\displaystyle alpha$₃=0 és a $\displaystyle beta$₁x+$\displaystyle beta$₂y+$\displaystyle beta$₃=0 egyenesek metszik egymást, akkor a hatványvonal -- tetszőleges u esetén -- átmegy a metszésponton. Ha az $\displaystyle alpha$₁x+$\displaystyle alpha$₂y+$\displaystyle alpha$₃=0 és a $\displaystyle beta$₁x+$\displaystyle beta$₂y+$\displaystyle beta$₃=0 egyenesek párhuzamosak, akkor a hatványvonal is -- u értékétől függetlenül -- párhuzamos velük.

A. 267. Legyen m, n pozitív egész és 0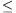x$\displaystyle le$1. Igazoljuk, hogy

(1-xⁿ)^m+(1-(1-x)^m)ⁿ$\displaystyle ge$1.

Vojtech Jarnik emlékverseny, Ostrava, 2000

1. megoldás. Az m=1 és n=1 esetekben tetszőleges xre egyenlőség áll. A továbbiakban feltesszük, hogy mn,>2.

Tekintsük az

f(x)=(1-xⁿ)^m+(1-(1-x)^m)ⁿ

függvényt. Behelyettesítéssel ellenőrizhető, hogy f(0)=f(1)=1.

Vizsgáljuk meg f deriváltjának viselkedését.

f'(x)=m(1-xⁿ)^m-1^.(-nx^n-1)+n(1-(1-x)^m)^n-1^.m(1-x)^m-1=

=mnx^n-1(1-x)^m-1^.(-(1+x+...+x^n-1)^m-1+

+(1+(1-x)+...+(1-x)^m-1)^n-1).

Az első tényező az intervallum belsejében mindig pozitív. A második tényező a 0-ban pozitív, az 1-ben negatív, és szigorúan monoton fogy. Ezért létezik egy olyan $\displaystyle 0<\xi<1$ valósz szám, hogy f' a $\displaystyle (0,\xi)$ intervallumban pozitív, a $\displaystyle (\xi,1)$ intervallumban pedig negatív. Az f függvény a $\displaystyle [0,\xi]$ szigorúan monoton nő, a $\displaystyle [\xi,1]$ intervallumban pedig szigorúan monoton fogy.

Kunszenti-Kovács Dávid és Csernenszki András

dolgozata alapján

2. megoldás. Töltsünk ki egy m sorból és n oszlopból álló táblázatot 0-kkal és 1-esekkel úgy, hogy minden mezőbe x valószínűséggel teszünk 1-est. Annak valószínűsége, hogy nincs csupa 1-esből álló sor, éppen (1-xⁿ)^m. Annak valószínűsége pedig, hogy nincs csupa 0-ból álló oszlop, éppen (1-(1-x)^m)ⁿ. Ha egyik esemény sem következne be, az azt jelentené, hogy van csupa 1-esből álló sor és csupa 0-kból álló oszlop is, ami lehetetlen. A két esemény közül tehát mindig bekövetkezik legalább az egyik, a valószínűségük összege ezért legalább 1.

Csóka Endre és Gerencsér Balázs

dolgozata alapján

A. 268. Egy szabályos 2n-szög n csúcsát pirosra, a többi csúcsát kékre színeztük. Nagyság szerint sorbarendezzük az összes piros pontpár távolságát, és nagyság szerint sorbarendezzük az összes kék pontpár távolságát is. Bizonyítsuk be, hogy az így kapott két, 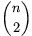${n\choose2}$ hosszúságú számsorozat ugyanaz.

Vojtech Jarnik emlékverseny, Ostrava, 2000

Megoldás. Csoportosítsuk az oldalakat és átlókat (a továbbiakban: éleket) a hosszuk szerint. Azt kell igazolnunk, hogy minden egyes csoportban ugyanannyi kék-kék él van, mint piros-piros.

Tekintsünk egy tetszőleges csoportot. Legyen a piros-piros, kék-kék, piros-kék élek száma rendre a, b, c. Az éleknek összesen 2a+c piros és 2b+c kék éle van. A sokszög minden csúcsa ugyanannyi csoportbeli élnek végpontja (ha a csoport a sokszög átmérőiből áll, akkor minden csúcs egy élnek végpontja; ellenkező esetben minden csúcs két csoportbeli élnek végpontja), ezért 2a+c=2b+c, amiből a=b.

Már regisztráltál?
Új vendég vagy?