A 2001. májusi számban kitűzött fizika elméleti feladatok megoldásai
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
P. 3437. 2 cm vastag, 0,5 kg/dm3 sűrűségű fakorong úszik a vizen.
a) Milyen vastag, ugyanolyan alapterületű alumíniumkorongot tehetünk a tetejére, hogy a fa ne legyen teljesen a víz alatt?
b) Mi a válasz akkor, ha alulra erősítjük fel az alumíniumkorongot? (3 pont)
Közli: Holics László, Budapest
Megoldás. Utaljon az 1-es index a fa-, a 2-es az alumíniumkorong adataira, és legyen \(\displaystyle rho\) a víz sűrűsége!
a) Határesetben, amikor a fakorong éppen bemerül a vízbe,
d1\(\displaystyle rho\)1+d2\(\displaystyle rho\)2=d1\(\displaystyle rho\), azaz d2=d1(\(\displaystyle rho\)-\(\displaystyle rho\)1)/\(\displaystyle rho\)2. Adatainkkal (\(\displaystyle rho\)1=0,5 kg/dm3, \(\displaystyle rho\)2=2,7 kg/dm3,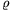 
=1 kg/dm3,
d1=2 cm) az alumíniumkorong vastagsága:
d2=0,37 cm.
b) Ilyenkor d1\(\displaystyle rho\)1+d2\(\displaystyle rho\)2=(d1+d2)\(\displaystyle rho\), azaz
\(\displaystyle d_2=d_1{\rho-\rho_1\over\rho_2-\rho}=0,59~\rm cm.\)
P. 3438. Rézből és nikkelből 1:1 arányú ötvözetet készítünk. Mekkora lesz az így keletkező ötvözet sűrűsége, ha a két fém térfogatváltozás nélkül elegyedik? (4 pont)
Közli: Tasnádi Péter, Budapest
Megoldás. A feladat szövegéből nem derül ki, hogy a keverési arány a tömegek arányára vonatkozik-e, vagy esetleg a térfogatok arányára utal. Vizsgáljuk meg mindkét esetet!
Ha a tömegarány 1:1, akkor
\(\displaystyle \bar{\rho}_1={2m\over m/\rho_1+m/\rho_2}={2\rho_1\rho_2\over\rho_1+\rho_2}.\)
Mivel \(\displaystyle rho\)1=8920 kg/m3, \(\displaystyle rho\)2=8900 kg/m3 \(\displaystyle \bar\rho_1\)=8910 kg/m3.
Ha a térfogatarány 1:1, akkor
\(\displaystyle \bar{\rho}_2={V\rho_1+V\rho_2\over2V},\)
azaz \(\displaystyle \bar\rho_2=8910~\rm kg/m^3\).
Megjegyzés. Bár \(\displaystyle \bar\rho_1\) és \(\displaystyle \bar\rho_2\) elvileg különböző mennyiségek, esetünkben a kétféle érték azért ilyen közeli (a különbség \(\displaystyle sim\)0,01 kg/m3, ami \(\displaystyle sim\)10\(\displaystyle ^{-4}\,\%)\), mert a két ötvözött anyag sűrűsége is nagyon közel van egymáshoz.
P. 3439. Egy 200 N/m rugóállandójú rugón két 1 kg-os test függ egy 10 cm hosszú fonállal összekötve, az ábrán látható módon. A fonalat elégetjük. Mekkora lesz a távolság a két test között, amikor a felső test először kerül legmagasabb helyzetébe?
(4 pont)
Közli: Szabó Zoltán, Budapest
Megoldás. A fonal elégetésekor a felső test a fölötte h=(mg/k) magasan levő pont körül \(\displaystyle T=2\pi\sqrt{m/k}\) periódusidejű, \(\displaystyle A=(mg/k)\,(=h)\) amplitúdójú harmonikus rezgőmozgásba kezd, míg az alsó test szabadon esik. A felső tömeg mozgásának legmagasabb pontja a kiindulás fölött 2A-val van, ezt a test T/2 idő alatt éri el először. Ezalatt az alsó test s=gT2/8 utat tesz meg, így a két test távolsága ekkor d=(mg/k)(2+\(\displaystyle pi\)2/2)+d0\(\displaystyle approx\)44 cm.
P. 3440. Légpárnás asztalon a kezdetben nyújtatlan, l0 hosszúságú húzó-nyomó rugó egyik vége rögzített, a másik végéhez egy m tömegű kis korongot erősítünk. Meglökjük a korongot a rugó hosszára merőlegesen, v0 kezdősebességgel. A kialakuló mozgás során a rugó legnagyobb megnyúlása \(\displaystyle Delta\)l=l0/10. Mekkora a rugóállandó? Vázoljuk fel a korong középpontjának pályagörbéjét!
(5 pont)
Közli: Simon Péter, Pécs
Megoldás. Amikor a rugó megnyúlása a legnagyobb, a sebesség éppen merőleges a sugárra, így a perdület megmaradása alapján
m0l0v0=m(l0+\(\displaystyle Delta\)l)v.
Ugyanakkor az energia-megmaradás tétele szerint
\(\displaystyle {1\over2}k(\Delta l)^2+{1\over2}mv^2={1\over2}mv_0^2.\)
Innen
\(\displaystyle k=mv_0^2{(2l_0+\Delta l)\over\Delta l(l_0+\Delta l)^2}\approx20{mv_0^2\over l_0\Delta l}.\)
A korong tömegközéppontjának mozgása jó közelítéssel egy \(\displaystyle omega\)=v0/(l0+\(\displaystyle Delta\)l/2) szögsebességű egyenletes körmozgásra, és sugár irányban \(\displaystyle T=2\pi\sqrt{m/k}\) periódusidejű harmonikus rezgőmozgásra bontható. A rezgés egy periódusa alatt a rugó szögelfordulása
\(\displaystyle \Phi=2\pi\sqrt{m\over k}\cdot{v_0\over l_0\left(1+{1\over20}\right)}={2\pi\over\sqrt{20}\left(1+{1\over20}\right)}\approx{2\pi\over4{,}7}.\)
A korong középpontja tehát egy l0 belső és \(\displaystyle l_0+\Delta l=1{,}1\,l_0\) külső sugarú körgyűrűben periodikusan ki-be mozog, pályája azonban nem zárt görbe, mert egy körülfordulás alatt 4,7 (tehát nem egész számú) rezgést végez.
P. 3441. Bizonyos mennyiségű egyatomos ideális gáz kétféleképpen jut el az ábrán látható A állapotból a B állapotba: vagy az AB, vagy az ACB úton. Az ACB úton a gáz által felvett hő csak 90 %-a az AB úton felvett hőnek. Kezdetben (az A állapotban) a gáz hőmérséklete 150 K. Mekkora a gáz hőmérséklete a C állapotban, és mekkora a B állapotban?
(5 pont)
Megoldás. A gáz adatai az egyes pontokban: TA=T0, pA=p0, VA=V0; TC=4T0, pC=p0, VC=4V0; TB=xT0, pB=xp0/4, VB=4V0, a mólok száma pedig mindig n. Feladatunk az x meghatározása. A hőfelvétel az ACB úton
QACB=ncp(TC-TA)+ncV(TB-TC).
Az AB úton felvett hő a belső energia megváltozásának és a tágulási munkának az összege, azaz
\(\displaystyle Q_{AB}=nc_v(T_B-T_A)+{p_A+p_B\over2}\left(V_B-V_A\right)\,.\)
A QACB=0,9QAB egyenletből (felhasználva, hogy cp=5R/2, cv=3R/2 és p0V0=nRT0) x=8 adódik, tehát TB=8T0=1200oK.
Közli: Kotek László, Pécs
P. 3442. A \(\displaystyle 2\,\ell\) hosszúságú tükör percenként 10-et fordul a tükör O felezőpontján átmenő, az ábra síkjára merőleges tengely körül. Az O középpontú, R sugarú kör A pontjában egy fényforrás, a B pontjában egy megfigyelő van (AOB\(\displaystyle szog\)=90o).
a) Milyen görbén mozog az A pontszerű fényforrás tükörbeli látszólagos képe?
b) Milyen sebességgel mozog A látszólagos képe?
c) Mekkora az \(\displaystyle R/\ell\) arány, ha a B megfigyelő a tükör \(\displaystyle phi\)=15o-os állásánál pillantja meg először a fényforrást?
d) Egyfolytában mennyi ideig láthatja a megfigyelő a tükörben a fényforrást ilyen \(\displaystyle R/\ell\) arány mellett?
(5 pont)
Közli: Gálfi László, Budapest
Megoldás. a) Az A fényforrás látszólagos képe az adott körön mozog.
b) A képe 1/(2f) idő alatt 2\(\displaystyle pi\).2f szögsebességgel fut be egy teljes kört, majd 1/(2f) ideig nincs kép, és ez ismétlődik.
Az ábráról (kihasználva, hogy egy adott húrhoz tartozó kerületi szög a középponti szög fele) leolvasható, hogy
\(\displaystyle \ell=R(\cos\varphi_0-\sin\varphi_0).\)
c) Esetünkben \(\displaystyle phi\)0=15o, így \(\displaystyle \ell/R=1/\sqrt{2}\).
d) Ha a B megfigyelő A képét \(\displaystyle phi\)0=15o-nál pillantja meg, a kép \(\displaystyle phi\)1=90o-15o=75o-nál fut ki a tükörből, ennek megfelelően a kép (\(\displaystyle phi\)1-\(\displaystyle phi\)0)/2\(\displaystyle pi\)f=1 s ideig látható egyfolytában.
P. 3443. Egy 100 eV mozgási energiájú elektron a lemezekkel 30o-os szöget bezáró sebességgel lép be két sűrű fémrácsból kialakított síkkondenzátor lemezei közé, és 45o-os szögben lép ki a lemezek közül.
Mekkora a kondenzátor feszültsége, és mekkora mozgási energiával hagyja el az elektron a kondenzátort?
(4 pont)
Közli: Varga István, Békéscsaba
Megoldás. A kondenzátoron való áthaladáskor a sebesség lemezekkel párhuzamos komponense nem változik, azaz
\(\displaystyle v\cos30^{\circ}=v^{\prime}\cos45^{\circ}.\)
A felvett energia:
\(\displaystyle {1\over2}mv^{\prime2}-{1\over2}mv^{2}=Ue\)
azaz
\(\displaystyle Ue={1\over2}mv^{2}\left({\cos^230^{\circ}\over\cos^245^{\circ}}-1\right)={1\over2}E_0=50~{\rm eV}.\)
Így U=50 V, és az elektron \(\displaystyle {3\over2}E_0=150\) eV energiával hagyja el a kondenzátort.
P. 3444. Egy ,,szuperellipszis'' egyenlete: (x/a)4+(y/b)4=1, ahol a és b a féltengelyek hossza.
Egy szuperellipszis keresztmetszetű homogén hengert nagyobb féltengelyével
függőleges helyzetben vízszintes asztallapra állítunk. Határozzuk meg
(numerikus, geometriai vagy analitikus módszerekkel), hogy mekkora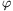 
szögű kibillentésig stabil az
ábrán látható helyzet! Ábrázoljuk \(\displaystyle phi\)-t a b/a ,,lapultsági arány'' függvényében!
(6 pont)
Közli: Gnädig Péter, Budapest
Megoldás. Tekintsük a szuperellipszis \(\displaystyle (x,\,y)\) és \(\displaystyle (x+\Delta x,\,y+\Delta y)\) pontjain átmenő húrját! Ennek meredeksége
\(\displaystyle m_{\rm h}={\Delta y\over\Delta x}.\)
Ha a \(\displaystyle Delta\)x-et es a \(\displaystyle Delta\)y-t minden határon túl csökkentjük (úgy hogy az \(\displaystyle (x+\Delta x,\,y+\Delta y)\) pont végig rajta marad a szuperellipszisen), a húr az \(\displaystyle (x,\,y)\) pontba húzható érintőbe, mh pedig az érintő mé meredekségébe megy át. Ennek kiszámításához felhasználjuk, hogy mind az \(\displaystyle (x,\,y)\), mind az \(\displaystyle (x+\Delta x,\,y+\Delta y)\) pont rajta van a szuperellipszisen, azaz
\(\displaystyle \left({x\over a}\right)^4+\left({y\over b}\right)^4=1,\)
és
\(\displaystyle \left({x+\Delta x\over a}\right)^4+\left({y+\Delta y\over b}\right)^4=1.\)
E két egyenlet különbségéből
\(\displaystyle m_{\rm h}={\Delta y\over\Delta x}=-{b^4\left(4x^3+6x^2(\Delta x)+4x(\Delta x)^2+(\Delta x)^3\right)\over a^4\left(4y^3+6y^2(\Delta y)+4y(\Delta y)^2+(\Delta y)^3\right)}.\)
Ha most \(\displaystyle Delta\)x-et és \(\displaystyle Delta\)y-t minden határon túl csökkentjük, ezek a mennyiségek és hatványaik nullává válnak, miközben a (\(\displaystyle Delta\)y/\(\displaystyle Delta\)x) hányados véges marad, így
\(\displaystyle m_{\rm é}=-{b^4x^3\over a^4y^3}.\)
A szuperellipszis középpontjából az \(\displaystyle (x,\,y)\) ponthoz húzott sugár meredeksége
\(\displaystyle m_{\rm s}={y\over x}.\)
A szuperellipszist kibillentve az egészen addig visszabillen, amíg az érintőnek az hosszabb szimmetriatengely felé mutató fele és az érintési ponthoz tartozó sugár hegyesszöget zárnak be egymással. A stabilitás határa az a pont, amelyben a sugár és az érintő merőlegesek egymásra, azaz
1+méms=0.
Innen a kérdéses \(\displaystyle phi\) szög tangense
\(\displaystyle {\rm tg}\,\varphi={x\over y}={a^2\over b^2}.\)
Megjegyzés. Érdekes, hogy a ,,csúcsára'' állított szuperellipszis tetszőlegesen nagy b/a lapultsági arány mellett stabil egyensúlyi helyzetben van, magától nem borul fel, hiszen a kritikus \(\displaystyle phi\) szög nem nulla (jóllehet b/a növelésével \(\displaystyle phi\) egyre kisebbé válik)! Ezzel a tulajdonsággal nem csak a feladatban szereplő alakú test, hanem minden (x/a)n+(y/b)n=1 egyenlettel leírt ,,hengeres test'' rendelkezik, amennyiben n>2.
Naiv (és hibás) érveléssel ennek az állításnak éppen az ellenkezőjére lehet következtetni. Képzeljünk el egy adott méretarányú szuperellipszist, melynek tömegközéppontja b magasan van az asztal lapja fölött. Ha a szuperellipszis legmélyebb pontjában a görbületi sugár R, és a testet egy kicsit kibillentjük, akkor az R-nél alacsonyabban fekvő pontjai az asztal síkjától eltávolodnak, az R-nél magasabban fekvők viszont közelednek az asztalhoz. A stabilitás feltétele nyilván az, hogy b<R teljesüljön.
Tételezzük fel, hogy a csúcsára állított szuperellipszisünk valamilyen a és b féltengelyek esetén stabil egyensúlyban van. Növeljük meg b-t n-szeresére, ekkor az R görbületi sugár n-edrészére csökken, s ha n elegendően nagy, akkor nb>R/n fog teljesülni, az ilyen méretarányú test tehát instabil.
Hol a hiba ebben a ,,levezetésben''?