A 2001. szeptemberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B. 3472. Hány olyan időpont van reggel 6 és este 6 óra között, amikor nem tudjuk kitalálni az óráról a pontos időt, ha nem tudjuk megkülönböztetni a nagy- és a kismutatót? (3 pont)

Kvant

Megoldás. Tegyük fel, hogy a óra b perckor a két mutató ugyanott áll, mint c óra d perckor, csak a kismutató és a nagymutató helye cserélődött fel. Itt 0$\displaystyle le$a,c$\displaystyle le$11 egész számok, 0$\displaystyle le$b,d<60 valós számok. (Az egyszerűbb számolás kedvéért 12 órát 0 órának tekintjük.) Ez azt jelenti, hogy 5a+b/12=d és 5c+d/12=a. Innen a és c segítségével b és d így fejezhető ki:

$\displaystyle b={60a+720c\over143},\quad d={60c+720a\over143}.$

Ha a=c, akkor b=d is fennáll, 0$\displaystyle le$a,c$\displaystyle le$11, a$\displaystyle ne$c esetén pedig mind b, mind d értékére 0 és 60 közé eső szám adódik. Ezért minden egyes 0$\displaystyle le$a$\displaystyle le$11 egész számra a óra és a+1 óra között pontosan 11 ilyen időpont van, reggel 6 és este 6 óra között pedig összesen 12^.11=132 ilyen időpont van.

B. 3473. A 2 egységnyi területű ABCD paralelogrammában az AD-vel párhuzamos egyenes a P és az R, az AB-vel párhuzamos egyenes pedig az S és a Q pontokban metszi a paralelogramma kerületét az ábra szerint. Mekkora az AQR, BRS, DPQ és CSP háromszögek területének összege? (3 pont)

Megoldás. Ha az AP=xAB és AS=yAD, akkor az ABQ háromszög területe y, az ARD háromszögé x, a CRQ háromszögé pedig (1-x)(1-y). Ennek alapján az AQR háromszög területe 2-x-y-(1-x)(1-y). A BSR, DPQ és CSP háromszögek területére hasonló gondolatmenettel rendre 2-(1-x)-y-x(1-y), 2-x-(1-y)-(1-x)y és 2-(1-x)-(1-y)-xy adódik. Ezeket összegezve a négy háromszög területének összege

8-2(x+(1-x))-2(y+(1-y))-(x+(1-x))(y+1-y))=3.

B. 3474. Határozzuk meg az 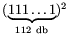$({\underbrace{111\dots1}_{112~{\rm db}}})^2$ hátulról számított hetvenharmadik számjegyét. (4 pont)

Megoldás. $\displaystyle {\underbrace{111\dots1}_{112}}^2$ hátulról számított hetvenharmadik számjegye megegyezik

$\displaystyle A={\underbrace{111\dots1}_{73}}+{\underbrace{111\dots1}_{72}}0+{\underbrace{111\dots1}_{71}}00+\ldots11{\underbrace{000\dots0}_{71}}+1{\underbrace{000\dots0}_{72}}$

hátulról számított hetvenharmadik számjegyével. Átalakítva

$\displaystyle A={10^{73}-1\over9}+10\cdot{10^{72}-1\over9}+10^2\cdot{10^{71}-1\over9}+\ldots+10^{71}\cdot{10^2-1\over9}+10^{72}\cdot{10-1\over9}=$

$\displaystyle 73\cdot{10^{73}\over9}-{1+10+\ldots+10^{72}\over9}=8\cdot10^{73}+{10^{73}-1\over9}-{1+10+\ldots+10^{72}\over9}+{1\over9}=$

$\displaystyle 8\cdot10^{73}+{8\over9}\cdot{\underbrace{111\dots1}_{73}}+{1\over9}=8\cdot10^{73}+{1\over9}\cdot{\underbrace{888\dots8}_{72}}9,$

ahonnan leolvasható, hogy a keresett számjegy 0.

B. 3475. Az a, b, c oldalú háromszög szögei $\displaystyle alpha$, $\displaystyle beta$, $gamma$ . Igazoljuk, hogy ha 3$\displaystyle alpha$+2 $beta$ =180^o, akkor a²+bc-c²=0. (4 pont)

Nemzetközi Magyar Matematika Verseny, 2001

Megoldás. A koszinusz-tétel alapján a²=b²+c²-2bccos $\displaystyle alpha$, ezért a bizonyítandó állítás ekvivalens a

b²=2bccos $\displaystyle alpha$-bc,

vagy bc-vel történő leosztás utan a szinusz-tételt is felhasználva a

$\displaystyle {\sin\beta\over\sin\gamma}=2\cos\alpha-1$

egyenlőséggel.

Felhasználva, hogy 3$\displaystyle alpha$+2$\displaystyle beta$=180^o=$\displaystyle alpha$+$\displaystyle beta$+$\displaystyle gamma$ látjuk, hogy $\displaystyle alpha$=2$\displaystyle gamma$-180^o és $\displaystyle beta$=360^o-3$\displaystyle gamma$. Ezért sin $\displaystyle beta$=-sin 3$\displaystyle gamma$ és cos $\displaystyle alpha$=-cos 2$\displaystyle gamma$, tehát a

$\displaystyle {-\sin3\gamma\over\sin\gamma}=-2\cos2\gamma-1$

összefüggést kell igazolnunk. Ez pedig leolvasható a

sin 3x=sin 2xcos x+sin xcos 2x=2sin xcos ²x+sin xcos 2x=sin x(2cos 2x+1)

egyenlőségből.

B. 3476. Egy szabályos 10 oldalú sokszög egy tetszőleges belső pontját a sokszög csúcsaival összekötve 10 darab háromszöget kapunk. A háromszögeket adott körüljárás szerint felváltva pirosra, illetve kékre festjük. Bizonyítsuk be, hogy a kék területek összege egyenlő a piros területek összegével. (4 pont)

1. megoldás. Az állítás nyilván igaz, ha a belső pont (a továbbiakban P) megegyezik a sokszög O középpontjával. Ha nem, akkor tegyük fel, hogy P az OAB háromszögben helyezkedik el, ahol A és B a sokszög két szomszédos csúcsa. Legyen Q az a pont, ahol a P-n át AB-vel húzott párhuzamos metszi az OA szakaszt (ez esetleg egybeeshet P-vel). Mind OQ, mind QP párhuzamos a sokszög egy-egy oldalával. Ezért elegendő azt belátni, hogy ha a P pontot a sokszög valamely oldalával párhuzamosan mozgatjuk, a kék háromszögek területének összege nem változik.

Ennek igazolásához először is vegyük észre, hogy az egyik ilyen háromszög alapja és magassága is változatlan marad. A másik négy háromszöget pedig két párba lehet osztani úgy, hogy egy páron belül a két háromszög alapja egy UVXY szimmetrikus trapéz két szárával (UV,XY) egyezik meg, ahol a P pont mozgatása éppen a trapéz VX,UY alapjaival párhuzamosan történik. Ha a P pont ezen trapéz pontja, akkor az UVP és XYP kék háromszögek területének összegét megkapjuk, ha a trapéz területéből kivonjuk az UYP és VXP háromszögek területét. Ez utóbbi két háromszög területe azonban nem változik, ha P-t alapjaikkal párhuzamosan elmozdítjuk. Ugyanígy érvelhetünk akkor is, ha P a trapézon kívül helyezkedik el, csak ebben az esetben az UYP és VXP háromszögek közül az egyiknek a területét nem kivonni kell a trapéz területéből, hanem ahhoz hozzáadni.

2. megoldás. Jelöljük a tízszög köré írt kör középpontjából a sokszög csúcsaiba mutató vektorokat a₁,a₂,...,a₁₀-zel, az adott belső pontba mutató vektort pedig p-vel.

A sokszög területe ekkor 5|a₁xa₂|, továbbá nyilván igaz, hogy a_ixa_i+1=a_i+1xa_i+2. Elegendő megmutatnunk, hogy a kék háromszögek területének kétszerese megegyezik a tízszög területével, azaz

|(a₁-p)x(a₂-p)+(a₃-p)x(a₄-p)+...+(a₉-p)x(a₁₀-p)|=5|a₁xa₂|.

Ez viszont azonnal adódik, ha a bal oldalon elvégezzük a műveleteket és felhasználjuk, hogy pxp=0 valamint a₁+a₂+...a₁₀=0.

B. 3477. Legfeljebb mekkora lehet a 2ⁿ fokos szög szinusza, ha n pozitív egész? (4 pont)

Megoldás. 2ⁿ fok szinusza csak attól függ, hogy 2ⁿ milyen maradékot ad 360-nal osztva. Mivel a sin x függvény a [0,$\displaystyle pi$] intervallumban $\displaystyle pi$/2-re szimmetrikus szigorúan konkáv nemnegatív függvény, a ($\displaystyle pi$,2$\displaystyle pi$) intervallumban pedig negatív, azt kell meghatároznunk, hogy 2ⁿ 360-nal vett osztási maradéka milyen közel lehet 90-hez, vagy ami ezzel ekvivalens, 2^n-3 45-tel vett osztási maradéka milyen közel lehet 11,5-höz. A 2 megfelelő hatványai 45-tel osztva sorban a következő maradékokat adják: 1/4,1/2,1,2,4,8,16,32,19,38,31,17,34,23,1, ettől kezdve a maradékok periodikusan ismétlődnek. Ezek közül a 8 van a legközelebb a 11-hez, tehát 2ⁿ fok szinuszának lehető legnagyobb értéke sin 64^o$\displaystyle approx$0,8988. Az is látszik, hogy ezt az értéket akkor kapjuk, ha n 12-vel osztva 6 maradékot ad.

B. 3478. Az ABC háromszög hozzáírt köreinek középpontjai O₁, O₂, O₃. Bizonyítsuk be, hogy O₁O₂O₃ háromszög területe legalább négyszerese ABC háromszög területének. (4 pont)

Javasolta: Besenyei Ádám, Budapest

B. 3479. Keressük meg a 6t²+3s²-4st-8t+6s+5 kifejezés minimumát. (4 pont)

Megoldás. A kifejezést átírhatjuk

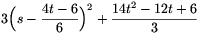
$3\Bigl(s-{4t-6\over6}\Bigr)^2+{14t^2-12t+6\over3}$

alakba. Ez rögzített t mellett nyilván akkor a legkisebb, ha s=2t/3-1, mely esetben értéke

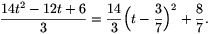
${14t^2-12t+6\over3}={14\over3}\Bigl(t-{3\over7}\Bigr)^2+{8\over7}.$

Ez pedig akkor a lehető legkisebb, ha t=3/7. A kifejezés minimuma tehát 8/7, melyet az s=-5/7, t=3/7 helyen vesz fel.

B. 3480. Adottak az e egyenesen az A, B, C és D pontok ebben a sorrendben. Mi azon P pontok mértani helye a síkban, amelyekre az APB és a CPD szögek egyenlők? (5 pont)

Gillis--Turán matematikaverseny, 2001.

Megoldás. Az e egyenes pontjai közül nyilván az AB és CD zárt szakaszokon kívül elhelyezkedő pontok lesznek jók. A továbbiakban tehát csak az egyenesen kívül eső pontokat vizsgáljuk. Ha az AB szakasz hossza megegyezik a CD szakasz hosszával, akkor nyilván az AD szakasz felező merőlegesén elhelyezkedő pontok megfelelők lesznek, és mondjuk látókörök segí tségével egyszerűen igazolható, hogy más pont nem lesz jó. A továbbiakban tehát azt is feltesszük, hogy AB $ne$ CD. Az APB és CPD szögek egyenlősége ekvivalens az APC és BPD szögek egyenlőségével. Ezért a keresett pontok megkaphatók úgy, hogy minden 0< $alpha$ < $pi$ esetén az e egyenes mindkét oldalán az AC és BD szakaszok fölé egyaránt $alpha$ szögű látóköríveket szerkesztünk és kijelöljük ezek metszéspontját.

Azt állítjuk, hogy van pontosan egy olyan körvonal, amelyre való inverzió az A pontot D-be, a B pontot pedig C-be viszi, és hogy a keresett pontok éppen ezen körvonal (e-n kívül eső) pontjai. Tegyük fel először, hogy k egy ilyen körvonal, ennek középpontja nyilván az e egyenesen van. Az inverzió szögtartó tulajdonsága miatt a k-ra vonatkozó inverzió az e egyenes mindkét oldalán kicseréli az AC és BD szakaszok fölé rajzolt $alpha$ szögű látóköríveket, ezek metszéspontjait tehát helybenhagyja, vagyis a metszéspontok valóban a k körön helyezkednek el. Világos, hogy a k kör minden e-n kívül eső pontját megkaphatjuk ilyen módon, és az is látszik ebből az érvelésből, hogy csak egyetlen ilyen k kör lehet, hiszen k-nak minden egyes látókörívvel alkotott metszéspontja egyértelműen meghatározott.

A keresett k kört pedig így határozhatjuk meg. Rajzoljunk az AC és BD szakaszok fölé egy-egy Thalesz-kört, és legyen P ezek egyik metszéspontja. Jelölje R a BC szakasz azon pontját, ahol a BPC szög felezője az e egyenest metszi. Mivel AB $ne$ CD, a PR szakasz nem merőleges e-re. Legyen O az e egyenesnek az a pontja, amelyre az ORP és OPR szögek megegyeznek. Egyszerű számolással adódik, hogy az OBP és OPC szögek is egyenlők, tehát az OBP háromszög hasonló az OPC háromszöghöz. Következésképpen OR²=OP²=OB^.OC. A konstrukcióból adódik, hogy PR egybeesik az APD szög felezőjével is, és ezért OR²=OA^.OD is igaz. A keresett k kör tehát éppen az O középpontú OR sugarú kör.

B. 3481. Legyen 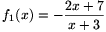$f_1(x)=-{{2x+7}\over{x+3}}$ , f_n+1(x)=f₁(f_n(x)). Határozzuk meg f₂₀₀₁(2002) értékét. (4 pont)

Megoldás.

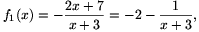
$f_1(x)=-{{2x+7}\over{x+3}}=-2-{1\over x+3},$

ezért

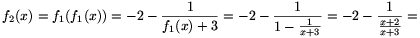
$f_2(x)=f_1(f_1(x))=-2-{1\over f_1(x)+3}=-2-{1\over{1-{1\over x+3}}}=-2-{1\over{x+2\over x+3}}=$

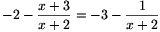
$-2-{x+3\over x+2}=-3-{1\over x+2}$

és

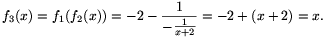
$f_3(x)=f_1(f_2(x))=-2-{1\over{-{1\over x+2}}}=-2+(x+2)=x.$

Ha pedig valamilyen k pozitív egész számra f_3k(x)=x, akkor f_3(k+1)(x)=f₃(f_3k(x))=f₃(x)=x is fennáll, ezért a teljes indukció elve alapján minden k pozitív egész számra f_3k(x)=x, f₂₀₀₁(2002)=2002, hiszen a számolásból az is leolvasható, hogy az f_i függvények az x=-2 és x=-3 helyeken kívül mindenütt értelmezve vannak.

Már regisztráltál?
Új vendég vagy?