A 2001. októberi számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3456. Egymással párhuzamosan fut egy vasúti sínpár, egy autópálya és egy kerékpárút. A középen levő autópályától 600 m távolságra van a vasút és 800 m-re a kerékpárút. A vonat sebessége 90 km/h, az autóé 60 km/h. Mindhárom jármű azonos irányban halad állandó sebességgel úgy, hogy az egyik pillanatban egy egyenesre illeszkednek. Mekkora a kerékpáros sebessége, ha ez az állapot fennmarad? (4 pont)

Közli: Simon Péter, Pécs

Megoldás: 20 km/h.

P. 3457. Egy edény színültig van víznél nagyobb sűrűségű, vízzel nem elegyedő, 0 C^o-os folyadékkal, benne úszik egy 0 C^o-os jégdarab. A hőmérsékletet 0 C^o-on tartva, a jégdarabot infravörös fénnyel megvilágítva elolvasztjuk. Kicsordul-e a víz a pohárból? (3 pont)

Közli: Varga István, Békéscsaba

Megoldás: A víz egy része kifolyik.

P. 3458. Mi a magyarázata annak, hogy ha egy farönkre nehéz teherrel súlyosbított balta élét illesztjük, alig-alig sérül meg a rönk, viszont ha a teher nélküli baltát felemeljük, és úgy sújtunk a rönkre, az széthasad? (3 pont)

Arisztotelész feladata nyomán

(,,Gondolatébresztő feladat'' a Sulineten)

Megoldás: A balta a súlyának sokszorosával hat a rönkre, amikor hirtelen lefékeződik.

P. 3459. Vízszintes felületen lévő m₁=0,6 kg tömegű és m₂=0,4 kg tömegű hasábokat könnyű, laza fonál köt össze. Az m₁ tömegű testet F=3 N nagyságú vízszintes erővel kezdjük húzni, és figyeljük a testek gyorsulását. A kísérletet több, különböző súrlódású felületen elvégezzük. A csúszási és a tapadási súrlódási együtthatót azonosnak tekintve $\displaystyle mu$ nullától 0,9-ig mindenféle értéket felvehet.

a) Adjuk meg és ábrázoljuk a testek gyorsulását függvényében!

b) Határozzuk meg és ábrázoljuk a fonálban fellépő erőnek a súrlódási tényezőtől való függését! (5 pont)

Közli: Kotek László, Pécs

Megoldás: a) A kötél megfeszülésekor bekövetkező rándulás után a két test gyorsulása megegyezik, és (g10 m/s²-tel számolva)

$\displaystyle a_1=a_2=\cases{{F\over m_1+m_2}-g\mu,{\rm\ ha\ }0\leq\mu\leq{F\over(m_1+m_2)g}=0{,}3;\cr\cr0{\rm\ k\ddot{u}l\ddot{o}nben.}\cr}$

b)

$\displaystyle K=\cases{{m_2\over m_1+m_2}F,{\rm\ ha\ }\mu<0{,}3;\cr\cr0,{\rm\ ha\ }0{,}5<\mu.\cr}$

Ha 0,3<$\displaystyle mu$<0,5, akkor a fonalat feszítő erő nagysága attól függ, hogy mekkora elmozdulás után állnak meg a testek (ezt pedig a fonal rugalmas tulajdonságai határozzák meg). Mindenesetre teljesülnie kell a tapadó súrlódás egyensúlyának megfelelő

F-m₁gKm₂g$\displaystyle mu$

egyenlőtlenségeknek.

P. 3460.  Egy lövedék sebességének meghatározására a h=0,8 m magas asztal szélére M=1,2 kg tömegű fakockát helyezünk, amelybe vízszintes irányból m=20 g tömegű lövedéket lövünk. (A lövedék benne marad a fakockában.) Az ütközés hatására a kocka lerepül az asztalról, és x=3 m távolságban ér talajt. Mekkora volt a lövedék sebessége? (4 pont)

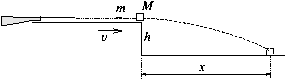
Megoldás:

$\displaystyle v=x\sqrt{{g\over2h}}{M+m\over m}\approx450~{{\rm m}\over{\rm s}}.$

P. 3461. Az ábrán vázolt kapcsolásban C helyére tetszőleges nagyságú kondenzátort tehetünk. Milyen határok között változtatható ezáltal az A és B pontok közötti kapacitás? (5 pont)

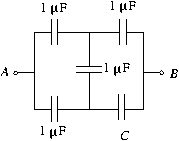
Közli: Légrádi Imre, Sopron

Megoldás: Az A és B pontok között az eredő kapacitás ($\displaystyle mu$ F egységekben számolva)

$\displaystyle C_{AB}={3+5C\over5+3C},$

amit

$\displaystyle C_{AB}={5\over3}-{16\over25+9C}$

alakban is felírhatunk. (C_AB kiszámításához felhasználhatjuk, hogy a bal oldali kör három ,,deltába'' kötött 1 $\displaystyle mu$F-os kapacitása helyettesíthető 3 darab ,,csillagba'' kapcsolt 3 $\displaystyle mu$F-os kondenzátorral. Az így kapott kapcsolásban már csak sorba és párhuzamosan kötött kondenzátorok vannak, de nincsen benne ,,híd''.) Eszerint

$\displaystyle {3\over5}\,\mu{\rm F}\leq C_{AB}\leq{5\over3}\,\mu{\rm F}.$

P. 3462.  Ugyanakkora elektromotoros erejű és egyaránt 3 $\displaystyle Omega$ belső ellenállású telepeket kapcsoltunk először párhuzamosan, majd sorosan egy 129 $\displaystyle Omega$-os fogyasztóra. Azt tapasztaltuk, hogy a soros kapcsolásnál egy-egy telep kapocsfeszültsége 10 %-kal kisebb, mint párhuzamos kapcsolás esetén.

a) Hány telepet használtunk?

b) Melyik esetben volt nagyobb a fogyasztón a teljesítmény? (4 pont)

Közli: Sütt Dezső, Budapest

Megoldás: a) A telepek száma n=5. b)

Sorosan kapcsolt telepeknél nagyobb a fogyasztón a teljesítmény.

P. 3463. Egyatomos ideális gázt térfogatának hetedrészére nyomunk össze, miközben nyomása hétszeresére nő egy olyan folyamatban, amelynek képe a p--V diagramon egy egyenes szakasz. A folyamat mely szakaszán vesz fel és mely szakaszán ad le hőt a gáz? Mennyi e két szakasz hosszának aránya a p--V diagramon? (5 pont)

Közli: Fári Jánosné, Szigetvár

Megoldás: A folyamat egyenlete a p-V diagramon

$\displaystyle p=p_0-{7p_0\over V_0}(V-V_0).$

Ebből a gáztörvény felhasználásával

$\displaystyle nR(T-T_0)=-6p_0(V-V_0)-{7p_0\over V_0}(V-V_0)^2.$

Egyatomos ideálos gáz esetén a belső energia megváltozása (miközben a (p₀, V₀) pontból az egyenes mentén a (p, V) pontba visszük a gázt) ennek a 3/2-e, azaz

$\displaystyle \Delta E_b=-9p_0(V-V_0)-{21p_0\over2V_0}(V-V_0)^2.$

Ezalatt a gáz által végzett tágulási munka

$\displaystyle L={p+p_0\over2}(V-V_0)=p_0(V-V_0)-{7p_0\over2V_0}(V-V_0)^2,$

a felvett hő pedig

$\displaystyle Q=\Delta E_b+L=-8p_0(V-V_0)-14{p_0\over V_0}(V-V_0)^2.$

Ennek a maximuma (amely pl. teljes négyzetté alakítással megkapható) V=5V₀/7-nél van. Ennek megfelelően amíg V>5V₀/7, addig a gáz hőt vesz fel, de ha már V<5V₀/7, akkor a gáz hőt ad vissza a környezetének. (Ugyanezt az eredmenyt úgy is megkaphatjuk, hogy megkeressük azt a pontot, ahol az adiabata görbe éppen érinti a folyamat egyenesét a p-V diagramon.)

A kérdéses szakaszok hosszának aránya 1:2.

P. 3464. Ha egy gázt melegítünk, előbb-utóbb világítani fog. Miért? (4 pont)

Közli: Kovács Gyula, Gyömrő

Megoldás: A gázmolekulák ütközésekor a kinetikus energia egy része a molekulák elektronhéját gerjeszti, az elektronhéj pedig a gerjesztett állapotból fénykibocsájtás mellett ugrik vissza az alapállapotba. Ehhez nyilván az kell, hogy az ütköző molekulák kinetikus energiája elég nagy legyen az elektronhéj gerjesztéséhez, azaz a hőmérséklet elég magas legyen.

P. 3465. Egy hosszú, keskeny csavarrugó annyira gyenge, hogy még saját súlya alatt is számottevően megnyúlik. Ezt a rugót egyszer az egyik végénél fogva függőlegesen lógatjuk, másszor mindkét végét tartjuk olyan távolságban, hogy a rugó az ábrán látható alakot vegye fel. Melyik esetben hosszabb a megnyúlt rugó? (6 pont)

Közli: Károlyházy Frigyes, Budapest

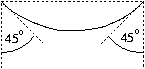
Megoldás: Az egyik végénél fogva függőlegesen lógatott rugóban az átlagos húzóerő mg/2, ennek megfelelően a megnyúlás mg/2k. Az ábrán látható esetben mindkét véget mg/2 függőleges, és ugyanekkora vízszintes erővel kell tartani. A rugót feszítő erő vízszintes komponense végig ugyanakkora, tehát mg/2. Az átlagos húzóerő így 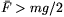, azaz a megnyúlás $\displaystyle Delta$x>mg/2k.

A megnyúlt rugó tehát a függőlegesen lógatott esetben lesz rövidebb.