A 2001. novemberi informatika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

I. 7. A Faktoriális(N) függvény rendkívül gyorsan növekszik. Míg az 5!=120, addig már a 10!=3 628 800 ábrázolásához 4 byte-os egész számokra van szükség. A 100! pedig már csak speciális matematikai programokkal kezelhető.

Tudjuk azonban, hogy minden természetes számnak elkészíthető a prímtényezős felbontása. Például:

5!=2³^.3^.5 10!=2⁸^.3⁴^.5²^.7.

Készítsünk programot, amely beolvassa billentyűzetről N értékét (1 $le$ N $le$ 10 000), majd kiírja a képernyőre az N! prímtényezős felbontását. (10 pont)

A feladat egy N szám faktoriális függvényének prímtényezős felbontásának elkészítése. Bemenő adat egy N természetes szám, mely legalább egy. A kimenő adat egy sorozat, mely szám-párokat tartalmaz, a prímosztókat, illetve azok multiplicitásait. Az össze prímet N-ig, olyan multiplicitással, hogy az összes szorzata N!-t adja.

Ehhez a feladatértelmezéshez (specifikáció) keresünk algoritmust.

Két megoldást is közlünk, melyeknek eredménye természetesen ugyanaz.

Az első megoldás értelmezése:


Konstans maxprím=5000;

Prím_felbontás = Rekord
                   Db   : Egész
                   elem : Tömb(1..maxprím): Rekord
                            prím, kitevő:   Egész
                          Rekord vége
                 Rekord vége

Változók
  fakt, akt : prím_felbontás
  i, j, n   : Egész

Beolvasunk egy számot. Ha a szám egy, akkor a felbontás is egy. Különben elkezdjük a számolást.


Be: N (1<=N<=10000)
Ha n=1
  Akkor Ki: 1
  Különben

Az első prím a 2, melynek a kitevője kezdetben 1.


    fakt.db:=1;
    fakt.elem[1].prím:=2;
    fakt.elem[1].kitevő:=1;

Majd 3-tól az összes számra N-ig kiszámoljuk a prímtényezős felbontását (Lásd az azonos nevű eljárásnál.)


    Ciklus i:=3-től n-ig
      Prímtényezők(i,akt);

Az új elem prímtényezős felbontásából származó kitevőket hozzá kell adni a már eddig kiszámolt kitevőkhöz.


    Ciklus j:=1-től akt.db-ig
      fakt.elem[j].kitevő:=fakt.elem[j].kitevő+akt.elem[j].kitevő;
    Ciklus vége

Ha újabb prím is szerepel - ami úgy lehet, hogy az új szám egy prím, ezért csak egyel nőhet a prímek száma egy lépésben -, akkor ezt az újabb elemet felvesszük a többi közé.


    Ha fakt.db<akt.db
      Akkor fakt.db:=fakt.db+1;
      fakt.elem[fakt.db]:=akt.elem[fakt.db];
     Elágazás vége
   Ciklus vége

Végül a faktoriális felbontásban szereplő összes elemet kiíratjuk.


   Ciklus i:=1-től fakt.db-ig
     Ki: fakt.elem[i].prím, fakt.elem[i].kitevő

Elágazás vége


Eljárás Prímtényezők(i : egész; akt : Prím_felbontás)

Használjuk a prím függvényt, hogy prím-e a szám.


  Függvény prím(j: Egész):Logikai

kettőtől kezdve a szám négyzetgyökéig osztót keresünk.


    k:=2
    Ciklus amíg (k*k<=j) és ((j mod k)>0)
      k:=k+1
    Ciklus vége

Mert, ha oszt, akkor nem prím, különben prím (elhagytuk a gyökét)


    prím:=(k*k>j)
  függvény vége

A 2 lesz az első prím, melynek kitevője kezdetben 1.


  j:=2;
  akt.db:=1;
  akt.elem[1].prím:=j;
  akt.elem[1].kitevő:=0;

Addig megyünk, amíg a prím kisebb vagy egyenlő a számmal.


  Ciklus amíg j<=i

Ha j osztója i-nek, akkor növeljük a kitevőt


   Ha i mod j=0
    Akkor akt.elem[akt.db].kitevő:=akt.elem[akt.db].kitevő+1
      i:=i div j;  és el is osztjuk.
    Különben j:=j+1;

de ha nem osztja, akkor megkeressük a következő nem nagyobb prímosztót.


     Ciklus amíg (j<=i) és nem prím(j)  nála
       j:=j+1;
     Ciklus vége

Ha találtunk prímet (legalább önmagát kellene), akkor eggyel több prím van


     Ha j<=i
       Akkor
     akt.db:=akt.db+1;

j lesz ez a prím nulla kitevővel, mert a következő ciklus elején majd eggyel növeljük ezt az értéket. (Akkor lesz egy.)


     akt.elem[akt.db].prím:=j;

     akt.elem[akt.db].kitevő:=0;
     elágazás vége
   Elágazás vége
 Ciklus vége

Ha az utolsó kitevő nulla, akkor azzal már nem kell számolnunk.


 Ha akt.elem[akt.db].kitevő=0
   Akkor akt.db:=akt.db-1;

eljárás
vége

Pascal program:

Program faktorialis;
  uses newdelay,crt;
  const maxprim=5000;
  type primfelbontas=record
                       db: integer;
                       elem: array [1..maxprim] of record
                                                     prim,kitevo: integer
                                                   end;
                     end;
  var fakt,akt: primfelbontas;
      i,j,n: integer;

  Procedure Primtenyezok(i: integer;var akt: primfelbontas);
    var j:integer;

    Function prim(j: integer): Boolean;
      var k: integer;
    begin
      k:=2;
      while (k*k<=j) and ((j mod k)>0) do k:=k+1;
      prim:=k*k>j;
    end;

  begin
    j:=2; akt.db:=1; akt.elem[1].prim:=j; akt.elem[1].kitevo:=0;
    while j<=i do
    begin
      if i mod j=0 then
      begin
        akt.elem[akt.db].kitevo:=akt.elem[akt.db].kitevo+1;
        i:=i div j;
      end
      else
      begin
        j:=j+1;
        while (j<=i) and not prim(j) do j:=j+1;
        if j<=i then
        begin
          akt.db:=akt.db+1;
          akt.elem[akt.db].prim:=j; akt.elem[akt.db].kitevo:=0;
        end;
      end;
    end;
    if akt.elem[akt.db].kitevo=0 then akt.db:=akt.db-1;
  end;
begin
  clrscr; writeln('                          Faktoriális számítás'); writeln;
  repeat
    write('Minek a faktoriálisát számoljam ki?'); readln(n);
  until (1<=N) and (n<=10000);
  writeln(n,'! felbontása:'); writeln;
  if n=1 then writeln(1) else
  begin
    fakt.db:=1; fakt.elem[1].prim:=2; fakt.elem[1].kitevo:=1;
    for i:=3 to n do
    begin
      Primtenyezok(i,akt);
      for j:=1 to akt.db do
        fakt.elem[j].kitevo:=fakt.elem[j].kitevo+akt.elem[j].kitevo;
      if fakt.db<akt.db then
      begin
        fakt.db:=fakt.db+1; fakt.elem[fakt.db]:=akt.elem[fakt.db];
      end;
    end;
    for i:=1 to fakt.db do write('prím=',fakt.elem[i].prim,
                                 '  kitevő=',fakt.elem[i].kitevo,' , ');
  end;
  readln;
end.

A második megoldás értelmezése:

A Legendre-formulát kódoljuk, ami a következő. Minden p prímre és N pozitív egészre igaz, hogy N! prímtényezős felbontásában a p kitevője

$\displaystyle \left[{N\over p}\right]+\left[{N\over p^2}\right]+\left[{N\over p^3}\right]+\dots$.

Természetesen ennek a sornak a tagjai valahonnan kezdve nullák, ugyanis N<pⁱ esetén az egészrész nulla lesz.)

Bekérjük a számot.


Be: N

Ha 1 a szám, akkor a felbontás is 1.


Ha N=1 Akkor Ki: 1

A legkisebb prím 2.


p:=2;

Ha a 2 nem nagyobb N-nél, akkor kiírjuk a 2-t és a kitevőjét.


Ha p<=N Akkor Ki: p,kitevő(p,N)

A következő prím a 3.


p:=3;

Amíg a prím nem nagyobb, mint a szám, addig írjuk ki a prímet, meg a kitevőjét. Majd megkeressük a következő prímet.


Ciklus amíg p<=N
  Ki: p,kitevő(p,N)
  KövetkezőPrím(p);
Ciklus vége

Program vége.

Egy prím kitevőjének kiszámítása a Legendre formulával.


Függvény kitevő(p,N:Egész):Egész

A kitevőben lesz a kiszámolt összeg; kezdetben 0.

pp-ben lesznek a p hatványai, kezdetben p.


  kitevő:=0
  pp:=p

Addig megyünk, amíg p egyik hatványa sem nagyobb, mint N.


  Ciklus amíg pp<=N

A kitevőt növeljük, és kiszámoljuk a következő hatványt.


    kitevő:=kitevő+Kerekít(n/pp)
    pp:=pp*p
 Ciklus vége

függvény
vége

A p-t követő prím megkeresése.


Eljárás KövetkezőPrím(p:Egész)

Használjuk a prím függvényt, hogy prím-e a szám.


  Függvény prím(j: Egész):Logikai

kettőtől kezdve a szám négyzetgyökéig osztót keresünk.


    k:=2
    Ciklus amíg (k*k<=j) és ((j mod k)>0)
      k:=k+1
    Ciklus vége

Ha oszt, akkor nem prím, különben prím (elhagytuk a gyökét)


    prím:=(k*k>j)
  függvény vége

Kettőt biztos léphetünk, mert csak a 2 páros prím. Így gyorsabb, hatékonyabb a program. Ezért választottuk szét a kettőt, majd az azt követő (páratlan) prímeket.


p:=p+2;

Amíg nem prím a szám, addig növeljük kettővel.


Ciklus amíg Nem prím(p)
  p:=p+2;
Ciklus vége

eljárás vége

Pascal program:

Program Faktorialis;
  Var
    N,p:LongInt;
  Function kitevo(pp,NN:LongInt):LongInt;
    Var
      k,ppp:LongInt;
  Begin
    k:=0;
    ppp:=pp;
    While ppp<=NN do begin
      k:=k+trunc(nn/ppp);
      ppp:=ppp*pp;
    end;
    kitevo:=k;
  end;
  Procedure KovetkezoPrim(Var p:LongInt);
    Function prim(j: LongInt): Boolean;
      var k: LongInt;
    begin
      k:=2;
      while (k*k<=j) and ((j mod k)>0) do k:=k+1;
      prim:=k*k>j;
    end;
  Begin
    p:=p+2;
    While Not prim(p) do
      p:=p+2;
  end;
Begin
  WriteLn('N faktorialis (N!) primtenyezos felbontasa:');
  WriteLn;
  Write('Add meg N értékét! :');
  ReadLn(N);
  WriteLn;
  WriteLn('A prímtényezős felbontás:');
  WriteLn;
  If N=1
    Then WriteLn(1);
  p:=2;
  If p<=N
    Then Write(p:5,' a ',kitevo(p,N):5,'-n    |');
  p:=3;
  While p<=N do begin
    Write(p:5,' a ',kitevo(p,N):5,'-n    |');
    KovetkezoPrim(p);
  end;
  ReadLn;
End.

I. 8. Egy kutya úgy úszik át a folyón a túlparton álló gazdájához, hogy minden pillanatban a gazdi irányába igyekszik. Ezt a mozgást kell közelítő módszerrel modellezni, és a képernyőre kirajzolnod. Ehhez a következő, valós értékű paramétereket kell beolvasnia a programnak a billentyűzetről:

(a) A folyó szélességét méterben.

(b) A gazda távolságát méterben a kutya kezdőpontjának vetületétől a túlparton (pozitív, ha a folyásiránnyal azonos irányban van, negatív az ellenkező esetben).

(d) A folyó sebességét (m/s, a folyó minden pontjában állandó nagyságú).

(e) A közelítés pontosságát, azaz annak az időintervallumnak a hosszát másodpercekben, amelyen belül a program egyenes vonalú mozgással számolhat.

A folyó két partját párhuzamos egyeneseknek tekintjük. A modellezés akkor álljon le, amikor a kutya már egy méternél közelebb kerül a túlsó parthoz.

Rajzoljuk ki a két partot jelző vízszintes egyeneseket, a kutya és a gazda kezdőhelyzetét és a kutya útját. (10 pont)

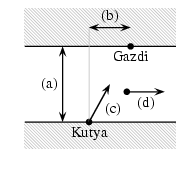
Ennek a szimulációnak az ábrázolásakor egyszerű átszámolási módszert használunk a valós koordinátarendszer és a képernyőn való megjelenítés tengelyei között. Egy méternek egy pixel fog megfelelni, illetve a képernyőn való ábrázolásnak megfelelően az x-tengely értékei jobbra nőnek, az y-tengely értékei pedig (a képernyő címzésének megfelelően, de a fizikában megszokottal ellentétben) a monitor alsó része felé nőnek.

Kódértelmezés:

Program

A változóink a feladat szövegének megfelelően:

   a,                        A folyó szélessége.
   b,                        A gazda távolsága a túlparton a vetülettől számolva.
   c,                        A kutya sebessége (mindig a gazdi fellé)
   d,                        A folyó sebessége (csak x irányba)
   e,                        A közelítés pontossága, időintervallum.
   t,                        Az eltelt időt számoljuk.
   szog,                     Milyen szögben úszik a kutya?
   gx,                       A gazdi x koordinátája.
   gy,                       A gazdi y koordinátája.
   kx,                       A kutya aktuális x koordinátája.
   ky:Valós;                 A kutya aktuális y koordinátája.
   hiba:Boolean;             Áll-e a kutya.

Ki: Kutya úszik a folyón.
Ki: Add meg a folyó szélességét!
Be: a
Ki: Add meg a gazdi távolságát a partra vetítve!
Be: b
Ki: Add meg a kutya sebességét!
Be: c
Ki: Add meg a folyó sebességét!
Be: d
Ki: Add meg az időlépés nagyságát!
Be: e
Grafikus_felület_megnyitása.

Felrajzoljuk a partvonalakat

Egyenes(10,10,KépernyőSzélesség-10,10)
Egyenes(10,Kerekít(a+10),KépernyőSzélesség-10,Kerekít(a+10));

Kör(20, Kerekít(a+10),2);            A kutya helye kezdetben.
Kör(Kerekít(20+b),10,2);             A gazdi helye
Kör(Kerekít(20+b),10,4);             kezdetben.
hiba:=HAMIS;                         Nincs hiba, vagyis feltételezzük, hogy úszik.

Ha c=0                               Ha mégsem úszik
  Akkor hiba:=IGAZ                   akkor baj van, nem ér oda.
  Különben                           különben OK
    kx:=20;                          A kutya kezdő
    ky:=a+10;                        helye
    gx:=20+b;                        A gazdi kezdő
    gy:=10;                          helye
    t:=0;
    SzínBeállítás(Piros);            Pirossal fog rajzolni
    Mozgat(Kerekít(kx),Kerekít(ky)); a kutya kezdő helyétől,
    Ciklus amíg ky-gy>1              egészen addig, amíg 1 méterre
                                     nem közelíti meg a partot.
      Ha gx-kx<>0                    Nullával nem lehet osztani.
        Akkor szog:=arctan((gy-ky)/(gx-kx))  A tangens miatt pedig kell,
        Különben szog:=pi/2;         de ekkor a szög éppen 90°.
      Ha szog>0
        Akkor szog:=szog+pi;

A sebesség vektor kirajzolása nem volt feladat. Ezt rajzoljuk kékkel, majd utána állítsuk vissza a színt pirosra.

      SzínBeállítás(Kék);
      Egyenes( Kerekít(kx),  Kerekít(ky),
               Kerekít(kx+10*c*cos(szog)), Kerekít(ky+10*c*sin(szog)));
      SzínBeállítás(Piros);

Az új x koordinátát úgy tudjuk kiszámolni, hogy ebben a kis intervallumban egyene s vonalú egyenletes mozgást feltételezünk, és ekkor a feladat szövegében is szerplő képletbe behelyettesítünk. Hasonlóan az y koordinátánal is.

      kx:=kx+(c*cos(szog)+d)*e;
      ky:=ky+c*sin(szog)*e;

Az új koordinátákig egyenes szakaszt kell húzni.

      EgyenesOdáig(Kerekít(kx),Kerekít(ky));

Az idő a kis intervallummal nő.

      t:=t+e;
    Ciklus vége
    ENTERre_vár
  Elágazás vége
Grafikus_felület_bezárása

Kiíratjuk az eredményt

Ha hiba
  Akkor Ki: Ha nem úszik, nem ér oda.
  Különben Ki: t,(kx-20-b);
ENTERre_vár

Program vége.

Pascal program:

Program Uszo_kutya;
  Uses
    Graph;
  Var
    gd,gm:Integer;
    a,b,c,d,e,t:Real;
    szog,gx,gy,kx,ky:Real;
    hiba:Boolean;
  Procedure OpenGraph;
  Begin
    DetectGraph(gd,gm);
    InitGraph(gd,gm,'c:\langs\bp\bgi');
  End;

Begin
  WriteLn('Kutya úszik a folyón.');
  Write('Add meg a folyó szélességét! :');
{  a:=200;{}
  ReadLn(a);
  Write('Add meg a gazdi távolságát a partra vetítve! :');
{  b:=100;{}
  ReadLn(b);
  Write('Add meg a kutya sebességét! :');
{  c:=5;{}
  ReadLn(c);
  Write('Add meg a folyó sebességét! :');
{  d:=6;{}
  ReadLn(d);
  Write('Add meg az időlépés nagyságát! :');
{  e:=1;{}
  ReadLn(e);
  OpenGraph;
  Line(10,10,GetMaxX-10,10);
  Line(10,trunc(a+10),GetMaxX-10,trunc(a+10));
  Circle(20,trunc(a+10),2);
  Circle(trunc(20+b),10,2);
  Circle(trunc(20+b),10,4);
  hiba:=FALSE;
  If c=0
    Then hiba:=True
    else begin
      kx:=20;
      ky:=a+10;
      gx:=20+b;
      gy:=10;
      t:=0;
      SetColor(Red);
      MoveTo(trunc(kx),trunc(ky));
      While ky-gy>1 do begin
        If gx-kx<>0
          Then szog:=arctan((gy-ky)/(gx-kx))
          Else szog:=pi/2;
        If szog>0
          Then szog:=szog+pi;
        SetColor(Blue);
        Line(trunc(kx),trunc(ky),trunc(kx+10*c*cos(szog)),trunc(ky+10*c*sin(szog)));
        SetColor(Red);
        kx:=kx+(c*cos(szog)+d)*e;
        ky:=ky+c*sin(szog)*e;
        LineTo(trunc(kx),trunc(ky));
        t:=t+e;
    {    ReadLn;{}
      end;
      ReadLn;
    End;
  CloseGraph;
  If hiba
    Then WriteLn('Ha nem úszik, nem ér oda.')
    else WriteLn(t:15:2,(kx-20-b):15:2);
  ReadLn;
End.{_Uszo_kutya}

I. 9. A binomiális együtthatók szokásos elrendezése (Pascal háromszög) az ábrán látható alakú lehet. A szélső elemek kivételével mindegyikre igaz, hogy a fölötte levő és az attól eggyel balra levő elem összege.

Készítsünk Excel táblázatot, amely ilyen módon képes megadni a Pascal háromszög első N+1 sorát! Az első sor hetedik cellájába lehessen beírni N értékét (1 $le$ N $le$ 20), és a táblázat minden esetben pontosan N+1 sorból álljon! (10 pont)

1						N=	6
1	1
1	2	1
1	3	3	1
1	4	6	4	1
1	5	10	10	5	1
1	6	15	20	15	6	1

A megoldás nagyon egyszerű, hiszen a Pascal háromszögről ismeretes, hogy egy elemét úgy kapjuk, hogy a két fölötte elhelyezkedőt összeadjuk. Most a táblázatunkban kicsit "megbillent" a háromszög, így a fölötte levő elemet és az amellettit kell összeadni.

Tehát a megoldás:

Az A oszlopban: =HA(SOR()<=$H$1+1;1;""), mindenhol vagy egyes szerepel, vagy semmi. Annak megfelelően, hogy N+1 sort kell kiírni, vagyis attól függően, hogy a sor sorszáma mennyi.

A többi helyre beírt képlet a következő: =HA(SOR()<=$H$1+1;C5+D5;""), hiszen itt is csak azokat a sorokat kell kiírni, ahol a sor sorszáma maximum N+1 ($H$1 helyen van N értéke), itt a példában a D6-os cellába beírt képlet szerint a a D5-ös és C5-ös cellák értékét kell összeadni.

Egyszerű a kitöltés is, hiszen automatikusan növeli az Excel a kitöltéskor a cellák sor- és oszlopazonosítóit. Arra kell csak vigyázni, hogy a második sorban ne legyen semmi a hatodik cellától kezdve, különben hibás lesz az egész háromszög, hiszen egy karakterrel nem tudunk összeadást végezni.

A megoldás letölthető innen.

Már regisztráltál?
Új vendég vagy?