 |
A 2002. márciusi számban kitűzött fizika elméleti feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
P. 3509. Lehetséges-e, hogy egy elejtett, szabadon eső test az esés utolsó másodpercében kétszer akkora utat tegyen meg, mint az ezt megelőző másodpercben? (3 pont)
Közli: Sütt Dezső, Budapest
Megoldás. Igen. 1,5 s és 2,5 s között a kő kétszer annyit esik, mint 0,5 s és 1,5 s között.
P. 3510. Egy 4 dm2 alapterületű, függőleges hengerben 32 g tömegű, 0 oC hőmérsékletű oxigéngázt 150 kg tömegű dugattyú zár el. A külső légnyomás 1,01.105 Pa. A henger tengelye függőleges, a dugattyú súrlódás nélkül mozoghat benne.
Milyen magasan áll a dugattyú? Mennyi hőt kell közölni a gázzal, hogy a dugattyú 20 cm-rel feljebb emelkedjék? (4 pont)
Bay Zoltán verseny, Sarkad
Megoldás. A hengerben levő gáz nyomása p=1,38.105 Pa, hőmérséklete T=273 oK, mennyisége pedig n=1 mol. Az általános gáztörvényből a térfogat, abból pedig a magasság megkapható: h=41 cm.
A dugattyú emelkedése közben a nyomás nem változik. A kétatomos gázok mólhőjének ismeretében a gáztörvény felhasználásával Q=(7/2)pΔV=3,86 kJ.
P. 3511. Függőleges falba vert szögön lóg egy l
hosszú fonálinga. Az ingát vízszintesen kitérítve tartjuk, majd
elengedjük. Amikor már a vízszinteshez képest  szöggel
elfordult, a fonál egy másik szögbe ütközik, s ettől kezdve a fonál
végén lévő kis test már e második szög körüli köríven folytatja
útját. Milyen messze lehet a második szög az elsőtől, ha a test az új
körpályán teljesen végigfut? (4 pont)
szöggel
elfordult, a fonál egy másik szögbe ütközik, s ettől kezdve a fonál
végén lévő kis test már e második szög körüli köríven folytatja
útját. Milyen messze lehet a második szög az elsőtől, ha a test az új
körpályán teljesen végigfut? (4 pont)
Közli: Farkas László, Keszthely
Megoldás. A kérdéses távolság
x≥l⋅33+2sinα.
P. 3512. Egy épület egyik oldalát erős napsugárzás éri. Milyen irányú huzat fúj át az épületen, ha a napos és az árnyékos oldalán is kinyitunk egy-egy ablakot? (3 pont)
,,Keresd a megoldást!'' verseny, Szeged
Megoldás. A hideg oldal felől a meleg felé: a meleg fal mellett felszálló áramlás alakul ki, és a felszálló meleg levegő helyére mindenhonnan - így a lakáson keresztül is - hidegebb levegő áramlik.
P. 3513. Becsüljük meg, hogy mekkora menetellenállást jelent
az autók számára az eső szélcsendben! Tegyük fel, hogy  óra alatt 10 mm csapadék esett, az
esőcseppek átmérője 2 mm, az autó homlokfelülete
1,5 m2, sebessége 90 km/h. Hogyan aránylik
egymáshoz az eső és a levegő sűrűsége? (5 pont)
óra alatt 10 mm csapadék esett, az
esőcseppek átmérője 2 mm, az autó homlokfelülete
1,5 m2, sebessége 90 km/h. Hogyan aránylik
egymáshoz az eső és a levegő sűrűsége? (5 pont)
Közli: Sári Péter, Budapest
Megoldás. A levegő átlagsűrűsége a benne levő esőcseppek miatt megnő, mondjuk Δ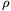 -val, ezért a közegellenállás is megnő kb. (1/2)A
-val, ezért a közegellenállás is megnő kb. (1/2)A
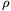 v2-tel. (A gépkocsi alaktényezőjét az egyszerűség kedvéért 1-nek vettük. Nagyságrendi becsléseknél az ilyen ,,nagyvonalúság'' megengedett.)
v2-tel. (A gépkocsi alaktényezőjét az egyszerűség kedvéért 1-nek vettük. Nagyságrendi becsléseknél az ilyen ,,nagyvonalúság'' megengedett.)
Úgy is érvelhetünk, hogy az autónak ütköző vízcseppeket az autó magával sodorja, így azoknak mv2/2 energiát kell adnia, az ehhez szükséges átlagos erő ugyancsak 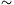 (1/2)A
(1/2)A
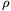 v2. (
v2. ( idő alatt az autónak ütköző víz tömege
idő alatt az autónak ütköző víz tömege 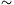

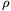 Av
Av , a víznek átadott energia
, a víznek átadott energia 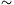 (1/2)
(1/2)
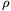 Av3
Av3 , mindez v
, mindez v úton.) (A kétféle gondolatmenettel kapott erőt nem szabad összeadni, hiszen mindkettő ugyanazt a fizikai jelenséget írja le.)
úton.) (A kétféle gondolatmenettel kapott erőt nem szabad összeadni, hiszen mindkettő ugyanazt a fizikai jelenséget írja le.)
A vízcseppek a levegőben a közegellenállás miatt már állandó sebességgel esnek. Ez a sebesség k=0,45 (a gömbre jellemző) közegellenállási tényezőt használva v0 7 m/s-nak adódik. Ha t=1800 s idő alatt h=10-2 m mennyiségű csapadék esik, az eső sűrűsége
7 m/s-nak adódik. Ha t=1800 s idő alatt h=10-2 m mennyiségű csapadék esik, az eső sűrűsége 
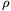 =
=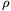 vh/v0t
vh/v0t 8.10-4 kg/m3. Innen
8.10-4 kg/m3. Innen  F
F 0,4 N.
0,4 N.
Az esővíz sűrűsége mintegy ezerszer kisebb, mint a levegő sűrűsége, s ennek megfelelően az általa okozott menetellenállás-változás is elhanyagolhatóan kicsi a levegő fékező hatásához képest.
P. 3514.  =30o hajlásszögű, két különböző felülettel
rendelkező, hosszú lejtő tetejéről kezdősebesség nélkül induló
m=4 kg tömegű, tömör henger mozgását
vizsgáljuk. A lejtő első szakasza nagyon sima, a súrlódási
tényező
=30o hajlásszögű, két különböző felülettel
rendelkező, hosszú lejtő tetejéről kezdősebesség nélkül induló
m=4 kg tömegű, tömör henger mozgását
vizsgáljuk. A lejtő első szakasza nagyon sima, a súrlódási
tényező  1=0, a második szakaszon pedig a súrlódási tényező
1=0, a második szakaszon pedig a súrlódási tényező
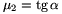 . Erre a felületre a henger akkor
érkezik, amikor a lejtőn haladva függőleges irányban már
h=1,8 m-t süllyedt.
. Erre a felületre a henger akkor
érkezik, amikor a lejtőn haladva függőleges irányban már
h=1,8 m-t süllyedt.

a) Az indítástól számítva mennyi idő múlva fog a henger tisztán gördülni?
b) Mennyi mechanikai energia vész el a henger mozgása során? (5 pont)
Közli: Kotek László, Pécs
Megoldás. a) t=1,8 s.
b)  E
E 36 J.
36 J.
P. 3515. Síkkondenzátor egy-egy lemezének területe
1500 cm2, a lemezek távolsága
20 mm. Rákapcsoltunk egy 250 V-os telepet, majd betoltunk a
lemezek közé, azokkal párhuzamosan egy 5 mm vastag fémlemezt és
egy ugyancsak 5 mm vastag üveglemezt ( rel=5). Mennyi munkát végeztünk a lemezek
betolása során? (5 pont)
rel=5). Mennyi munkát végeztünk a lemezek
betolása során? (5 pont)
Zemplén Győző verseny, Nagykanizsa
Megoldás. Egy síkkondenzátor kapacitása C= 0
0 rA/d. Először A=0,15 m2, d=0,02 m, és
rA/d. Először A=0,15 m2, d=0,02 m, és  rel=1. A h=5 mm vastag fémlemez betolása olyan, mintha a fegyverzetek távolsága d-h=0,015 m-re csökkenne (még akkor is, ha a betolt lemez nem ér hozzá a fegyverzetek egyikéhez sem, azaz két légrés keletkezik). Az üveg betolása után a rendszer úgy adható meg, mintha két sorba kötött kondenzátorunk lenne, egyikben a fegyverzetek távolsága d-2h=0,01 m és
rel=1. A h=5 mm vastag fémlemez betolása olyan, mintha a fegyverzetek távolsága d-h=0,015 m-re csökkenne (még akkor is, ha a betolt lemez nem ér hozzá a fegyverzetek egyikéhez sem, azaz két légrés keletkezik). Az üveg betolása után a rendszer úgy adható meg, mintha két sorba kötött kondenzátorunk lenne, egyikben a fegyverzetek távolsága d-2h=0,01 m és  rel=1, a másikban a távolság
rel=1, a másikban a távolság  , és
, és  rel=5. Ennek alapján az eredő kapacitások
rel=5. Ennek alapján az eredő kapacitások
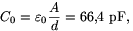
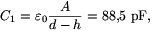
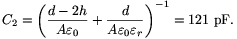
A lemezek betolása során a kondenzátor energiája előbb
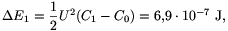
utóbb pedig
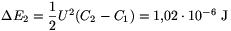
értékkel nő.
Ez az energianövekedés azonban nem egyezik meg az általunk végzett munkával, hiszen a telep is végez munkát. A kondenzátoron levő töltés kezdetben
Q0=1,66.10-8 C,
a fémlemez betolása után pedig
Q1=2,21.10-8 C.
a telep által végzett munka
=(Q1-Q0) U=13,8.10-7 J,
ez éppen kétszerese a kondenzátor energianövekedésének. A telep tehát amellett, hogy a kondenzátor energiáját növelte, rajtunk (a lemezt betolókon) is végzett valamennyi, nevezetesen W1=6,9.10-7 J-nyi munkát. Hasonlóan az üveglemez betolásakor sem kellett (pozitív) munkát végezzünk, az általunk végzett munka W2=-1,02.10-6 J.
A negatív munkavégzésből arra következtethetünk, hogy a kondenzátor (a szélén levő inhomogén elektromos mező miatt) vonzóerőt fejt ki a fémlemezre is és az üveglemezre is.
P. 3516. Az ábrán látható négyzetes keresztmetszetű gyűrű egyik fele rézből, másik fele alumíniumból készült. A gyűrű belső sugara 8 cm, külső sugara 10 cm, és bemerül egy, a síkjára merőleges, 0,1 T indukciójú homogén mágneses térbe.

Mekkora töltés halmozódik fel az összeillesztéseknél, ha a mágneses indukció értékét 2 másodperc alatt egyenletesen zérusra csökkentjük? (6 pont)
Közli: Pálfalvi László, Pécs
Megoldás. A kétféle fém eltérő fajlagos ellenállását  1-gyel, illetve
1-gyel, illetve  2-vel jelölve
2-vel jelölve
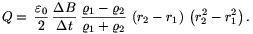
A megadott számadatokkal, továbbá az alumínium és a réz vezetőképességének táblázatban megtalálható értékeivel
Q 5.10-18 As
5.10-18 As
adódik. Ez 31,3 elemi töltésnek felel meg, ami annyit jelent, hogy körülbelül 31 vagy 32 többlet-elektron jelenik meg az egyik összeillesztésnél, a másiknál pedig ugyanennyi elektronhiány alakul ki.
P. 3517. Egy radioaktív sugárforrás felezési ideje T, s kezdetben r0 távolságra van a mérőműszerünktől. Egyszer csak elindul felénk úgy, hogy mérőműszerünkön a beütésszám nem változik.
Adjuk meg a sugárforrás és a műszer közötti távolságot az idő függvényében! Mekkora volt a radioaktív forrás kezdősebessége? (A levegő abszorpciós hatásától tekintsünk el!) (5 pont)
Közli: Simon Péter, Pécs
Megoldás. A sugárforrástól r távolságra mért beütésszám
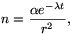
ahol  egy arányossági tényező és
egy arányossági tényező és  =ln 2/T a bomlásállandó.
=ln 2/T a bomlásállandó.
Ha a mért beütésszám állandó,
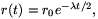
ahol r0 a forrás és a detektor távolsága a t=0 időpillanatban. Innen a kezdősebesség differenciálással, vagy az exponenciális függvény 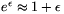 (ha
(ha 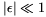 ) közelítésével
) közelítésével
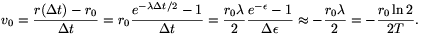
P. 3518. A XIX. században a Napot égő széntömbnek vélték, amely sugárzása által veszíti el energiáját. A napsugárzás intenzitása a Földön 1400 W/m2. Tételezzük fel, hogy ez az intenzitás a jövőben sem csökken! A Nap tömege 2.1030 kg, távolsága a Földtől 1,5.1011 m, a szén fűtőértéke 30 MJ/kg.
Mennyi ideig sütne még a Nap, ha valóban égő szénből állna? (A számítás eredménye a korabeli tudósokat is meglepte.) (4 pont)
Közli: Korpássy Péter, Budapest
Megoldás. Az égő széngömb-hipotézis szerint a Nap rendelkezésre álló teljes energiája 6.1037J lenne. Ez a feltételezett intenzitás (kb. 4,0.1026 W) mellett 1,5.1011 s-ra, vagyis kb. 4800 évre elegendő. Ez a meglepő szám szerepel Madách drámájában, Az ember tragédiája tizenharmadik színében:
| ,,S feledted-é már a tudós szavát, Ki felszámolta, hogy négyezredévre Világod megfagy, - a küzdés eláll?'' |
P. 3519. Az ábra szerinti összeállításban az alsó henger dugattyúja kezdetben 10 cm magasan áll, alatta 20 oC-os nitrogén, felette higany, amely kitölti a gumicsövet, és a felső edényben van a szabad felszíne, 2 méterrel a dugattyú felett. A henger alapterülete 100 cm2, a dugattyú súlytalan, és a nitrogén 30 cm magasságig tágulhat. A külső légnyomás 105 Pa.

A nitrogént melegítjük, és miközben a dugattyú emelkedik, a felső edényt folyamatosan süllyesztjük oly módon, hogy amíg a dugattyú 1 mm-t emelkedik, azalatt a higany felső szintje 9 mm-rel kerüljön lejjebb. Ezt addig folytatjuk, amíg a nitrogén hőt vesz fel.
Mennyi a felvett hő? Mekkora a nitrogén legnagyobb hőmérséklete? (6 pont)
Közli: Légrádi Imre, Sopron
Megoldás. Q=568 J, Tmax=374 K.

