A 2002. áprilisi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3542.Bizonyítsuk be, hogy ha egy 111...1 alakú szám osztható 7-tel, akkor osztható 37-tel is. (3 pont)

Megoldás. Könnyen ellenőrizhető, hogy az 1, 11, 111, 1111, 11111 és 111111 számok közül egyedül a 111111 osztható 7-tel, 37-tel pedig ezen kívül még a 111 osztható. Ha n=6q+r akkor az n számú 1-esből alló N szám 10^rQ+R alakba írható, ahol Q és R rendre a 6q illetve r számú 1-esből alló számot jelölik. Itt Q osztható 111111-gyel, hiszen Q=111111^.(1+10⁶+...+10^6(q-1)), és ezáltal 7-tel, valamint 37-tel is. R viszont csak akkor osztható 7-tel, ha r=0. N tehát pontosan akkor osztható 7-tel, ha n osztható 6-tal, és ekkor N=10^rQ 37-tel is osztható lesz.

B.3543.Egy négyzet alakú papírlapon egy négyzet alakú lyuk van. A lyuk mindegyik oldalát meghosszabbítottuk pozitív körüljárás szerinti irányban. Tegyük fel, hogy az így kapott félegyenesek a papírt négy négyszögre bontják az ábra szerint. Igazoljuk, hogy ebből a négy négyszögből másképpen is összeállítható egy négyzet, amelyben van egy négyzet alakú lyuk.

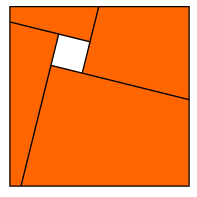
(4 pont)

Gál Péter ötletéből

Megoldás. Vezessük be az alábbi ábrán látható jelöléseket.

Rögzítsük most a KHJC négyszöget, és toljuk el az LEKD négyszöget úgy, hogy annak L csúcsa J-be kerüljön. Az E,K,D csúcsok képét jelölje rendre E', K' és D'; ekkor világos, hogy a C pont a JD' szakasz belsejében helyezkedik el. Ezután toljuk el az AIFL négyszöget is úgy, hogy annak I csúcsa a K' pontba kerüljön, és jelölje az A,F,L csúcsok képét rendre A', F' és L'. Ekkor nyilván D' az A'K' szakasz belső pontja lesz. Végül jelölje az F'L' és HK egyenesek metszéspontját G', az L'A' és KC egyenesek metszéspontját pedig B'. Ilyen módon a következő ábrát kapjuk:

Először is megmutatjuk, hogy a KB'L'G' négyszög egybevágó az IBJG négyszöggel. Legyen EF=FG=GH=HE=a, IB=b, JC=c, KD=d, LA=e, AI=p, BJ=q, CK=r, DL=s, FI=x, GJ=y, HK=z és EL=v. Mivel a H,E' és F' csúcsoknál derékszög van, a HE'F'G' négyszög téglalap. Ezért

G'L'=G'F'-L'F'=HJ+JE'-L'F'=(a+y)+v-(v+a)=y=GJ,

és hasonlóképpen G'K=GI. A G'L'K derékszögű háromszög tehát egybevágó a GJI háromszöggel, sőt, abból párhuzamos eltolással származtatható. Mivel az L'B' és KB' szakaszok is rendre párhuzamosak a JB és IB szakaszokkal, a KL'B' és IJB háromszögek is egybevágók, ami állításunkat igazolja.

Annyit kell már csak megmutatnunk, hogy a HE'F'G' és A'B'CD' négyszögek valójában négyzetek. Mivel mindkét négyszög téglalap, azt kell csak igazolni, hogy HE'=E'F' és B'C=CD'. HE'=(a+y)+v és E'F'=(z+a)+x miatt az első egyenlőség ekvivalens az y+v=z+x egyenlőséggel, először tehát ezt igazoljuk. Jelöljük ehhez az FLD szöget $\displaystyle alpha$-val, ekkor

AB=(LE+HJ)sin$\displaystyle alpha$-EHcos$\displaystyle alpha$=(y+v)sin$\displaystyle alpha$+a(sin$\displaystyle alpha$-cos$\displaystyle alpha$),

és hasonlóképpen BC=(z+x)sin$\displaystyle alpha$+a(sin$\displaystyle alpha$-cos$\displaystyle alpha$), ahonnan AB=BC miatt y+v=z+x következik. A második egyenlőséghez pedig azt kell igazolnunk, hogy r-b=s-c; r+d=e+s miatt ez ekvivalens a b+d=e+c egyenlőséggel. Azonban

b+d=AB-(z+x)cos$\displaystyle alpha$-a(sin$\displaystyle alpha$+cos$\displaystyle alpha$)

és

e+c=BC-(y+v)cos$\displaystyle alpha$-a(sin$\displaystyle alpha$+cos$\displaystyle alpha$),

ahonnan AB=BC és y+v=z+x miatt a keresett egyenlőség leolvasható.

B.3544. Mutassuk meg, hogy a háromszög hozzáírt körei közt van olyan, amelynek a sugara legalább háromszorosa a beírt kör sugarának. (3 pont)

Megoldás. A szokásos jelölések megtartásával feltesszük, hogy a háromszög oldalaira a$\displaystyle le$b$\displaystyle le$c teljesül, ekkor 2s=a+b+c$\displaystyle ge$3a$\displaystyle ge$3(a+b-c)$\displaystyle ge$3(2s-2c) miatt s$\displaystyle ge$3(s-c). Jelölje az O középpontú beírt körnek az a oldalon lévő érintési pontját E, a c oldalhoz hozzáírt O_c középpontú körnek az a oldal egyenesén lévő érintési pontját pedig F. Ekkor CE=s-c és CF=s. Az O és az O_c pont is a C csúcsból induló szögfelezőn helyezkedik el. Ezért a COE és CO_cF derékszögű háromszögek hasonlók, ahonnan a c oldalhoz hozzáírt kör és a beírt kör sugarának arányára r_c/r=O_cF/OE=CF/CE=s/(s-c)$\displaystyle ge$3 leolvasható.

B.3545. Bizonyítsuk be, hogy

$\displaystyle {n^2-n\over2}\leq\big\{\sqrt1\big\}+\big\{\sqrt2\big\}+\ldots+\big\{\sqrt{n^2}\big\}\leq{n^2-1\over2},$

ahol {x} az x törtrészét jelöli. (4 pont)

Megoldás. Az alsó becsléshez állítsuk párba az n² tagú összeg elemeit a 0-val egyenlő $\displaystyle \{\sqrt1\}$, $\displaystyle \{\sqrt4\},\ldots,\{\sqrt{n^2}\}$ számok kivételével úgy, hogy az egy párban lévő számok összege ne legyen kisebb 1-nél. A keresett párbaállítás lehetősége azonnal következik a $\displaystyle \{\sqrt{k^2+i}\}+\{\sqrt{(k+1)^2-i}\$1"> egyenlőtlenségből, mely tetszőleges k pozitív egész és 1$\displaystyle le$i$\displaystyle le$k esetén fennáll. Az egyenlőtlenség igazolásához jelöljük a baloldalon szereplő két számot $\displaystyle alpha$-val és $\displaystyle beta$-val, 0<$\displaystyle alpha$,$\displaystyle beta$<1. Ekkor k²+i=(k+$\displaystyle alpha$)² és (k+1)²-i=(k+$\displaystyle beta$)². Összegzés után mindkét oldalból 2k²-et kivonva a

2k+1=2k($\displaystyle alpha$+$\displaystyle beta$)+$\displaystyle alpha$²+$\displaystyle beta$²<(2k+1)($\displaystyle alpha$+$\displaystyle beta$)

egyenlőtlenséghez jutunk, ami bizonyítja az állítást.

A felső becsléshez vegyük észre, hogy 1$\displaystyle le$i$\displaystyle le$2k esetén

$\displaystyle \Bigl(k+{i\over2k}\Bigr)^2=k^2+i+\Bigl({i\over2k}\Bigr)^$k^2+i\ ,">

ahonnan \(\displaystyle \{\sqrt{k^2+i}\}k<n esetén a szóban forgó i-kre összegezve kapjuk, hogy a feladatban szereplő összeg nem nagyobb, mint

$\displaystyle \sum_{k=1}^{n-1}\sum_{i=1}^{2k}{i\over2k}=\sum_{k=1}^{n-1}{2k+1\over2}={n^2-1\over2}\ .$

B.3546. Egy kockát egy síkkal metszve olyan ABCDEF hatszöget kapunk, amelynek AD, BE, CF átlói egy ponton haladnak át. Bizonyítsuk be, hogy a metsző sík áthalad a kocka középpontján. (5 pont)

Megoldás. Először is vegyük észre, hogy a hatszög egymással szemközti oldalai a kocka egymással párhuzamos, szemközti lapjain helyezkednek el, és ennek következtében egymással párhuzamosak. Ha az átlók metszéspontját O-val jelöljük, akkor tehát az AOB háromszög hasonló a DOE háromszöghöz, a BOC háromszög hasonló az EOF háromszöghöz, a COD háromszög pedig hasonló az FOA háromszöghöz.

Tegyük fel, hogy a hatszög valamelyik szemközti oldalpárja nem egyenlő hosszúságú, mondjuk AB<DE. Ekkor az AOB és DOE háromszögek hasonlósága miatt OA<OD és OB<OE is igaz. A BOC és EOF háromszögek hasonlóságából OB<OE miatt az OC<OF egyenlőtlenségre következtethetünk, ahonnan a COD és FOA háromszögek hasonlósága az OD<OA egyenlőtlenségre vezet, ami ellentmondás.

Megállapíthatjuk tehát, hogy AB=DE. A DE oldalt taltalmazó lapon azonban csak legfeljebb kettő olyan szakasz található, amely az AB-vel párhuzamos, és azzal egyenlő hosszúságú. Ezek közül az egyik, melyet az AB oldalnak a kocka AB oldalt tartalmazó lappal párhuzamos szimmetriasíkjára való tükrözésével kapunk, nem jöhet szóba, ekkor ugyanis a kocka síkmetszete egy négyszög lenne. A szóba jövő másikat viszont úgy kapjuk, hogy az AB oldalt a kocka középpontjára tükrözzük, következésképpen az ABDE sík áthalad a kocka középpontján.

B.3547. Bizonyítsuk be, hogy ha az f függvényre

$\displaystyle f(x+1)+f(x-1)=\sqrt2f(x)$

minden valós x-re teljesül, akkor a függvény periodikus. (4 pont)

Megoldás. Az összefüggést először x helyett az x+3 és x+1 számokra, majd az x+2 számra alkalmazva látható, hogy minden valós x-re

$\displaystyle f(x+4)+2f(x+2)+f(x)=\sqrt{2}f(x+3)+\sqrt{2}f(x+1)=2f(x+2)\ ,$

vagyis f(x+4)+f(x)=0. Ezért minden valós x-re f(x+8)=-f(x+4)=f(x), tehát az f függvény valóban periodikus, egyik periódusa pedig 8.

B.3548. Egy különböző pozitív egészekből álló végtelen számtani sorozat minden elemét elosztjuk a legnagyobb prímosztójával. Lehet-e az így kapott sorozat korlátos? (4 pont)

Megoldás. Tegyük fel, hogy a kapott sorozat korlátos, és jelöljük ekkor maximumát M-mel. M=a/p, ahol a az eredeti S sorozat egy eleme, p pedig a legnagyobb prímosztója. Legyen az S sorozat differenciája d, ekkor d szükségképpen pozitív egész. Tekintsük most az S sorozat b=a+ad elemét, jelölje ennek legnagyobb prímosztóját q. Mivel b osztható a-val, és így p-vel is, q$\displaystyle ge$p. Ha q=p, akkor b/q=(a+ad)/p>a/p=M, ami nem lehetséges. Ha pedig q>p, akkor a nem osztható q-val, és ezért b/q=(1+d)a/q osztható a-val. Ekkor azonban b/q$\displaystyle ge$a>a/p=M, ami ismét csak lehetetlen. Ezért kiindulási feltevésünk nem lehet helyes, a kapott sorozat biztosan nem korlátos.

B.3549. Bizonyítsuk be, hogy tetszőleges x valós szám esetén

cos cos x$\displaystyle ge$|sin x|.

(4 pont)

Javasolta: Szobonya László, Budapest

I. megoldás. Mivel mindkét függvény 2$\displaystyle pi$ szerint periodikus páros függvény, elegendő az állítást a [0,$\displaystyle pi$] intervallumban igazolni. Továbbá |sin($\displaystyle pi$-x)|=|sinx| és coscos($\displaystyle pi$-x)=cos(-cosx)=coscosx, ezért elegendő az I=[0,$\displaystyle pi$/2] intervallumra szorítkozni. Ebben az intervallumban |sinx|=cos($\displaystyle pi$/2-x), a koszinusz függvény pedig monoton csökken. Ezért elegendő azt észrevenni, hogy x$\displaystyle in$I esetén cosx és $\displaystyle pi$/2-x is az I intervallumhoz tartozik, és f(x)=cosx$\displaystyle le$ $pi$ /2-x=g(x). Ez az egyenlőtlenség azonban azonnal következik abból, hogy f( $pi$ /2)=g( $pi$ /2)=0, és az I intervallumban ezen függvények deriváltjaira f'(x)=-sinx $ge$ -1=g'(x) teljesül.

II. megoldás. Legyen cosx=y. -1 $le$ cosx $le$ 1 minden x-re, ezért -1 $le$ y $le$ 1 is igaz lesz. Ezért cosy>0. Vegyük az egységkört, és rajta azt a P pontot, melynek a vízszintes tengelytől mért távolsága |siny|. A P-től a tengelyig érő |y| hosszúságú körív szintén P-t köti össze a tengely egy pontjával, ez az út viszont csak hosszabb lehet, hiszen a pont és az egyenes távolsága a ponttól az egyenesig vezető utak közül a legrövidebb. Tehát |siny| $le$ |y|. Mindkét oldal nemnegatív, ezért négyzetre emelve: sin²y $le$ y². Mivel sin²y+cos²y=1, ezért 1-cos²y $le$ y², és így cos²y $ge$ 1-y². 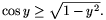Mivel -1 $le$ y $le$ 1, ezért y² $le$ 1, így az egyenlet mindkét oldalán nemnegatív szám áll, így kihasználva, hogy a négyzetgyök-függvény szigorúan monoton, valamint, hogy cosy>0: $\cos y\geq\sqrt{1-y^2}.$

Ezután y helyébe cosx-et beírva: 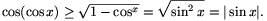$\cos(\cos x)\geq\sqrt{1-\cos^x}=\sqrt{\sin^2x}=|\sin x|.$ Ezzel a feladat állítását beláttuk.

Backhausz Ágnes (Budapest, Fazekas Mihály Fővárosi Gyakorló Gimnázium, 11. o. t.) megoldása alapján

B.3550.Az ABC háromszög A-ból és B-ből induló magasságvonalai az M pontban metszik egymást, a szemközti oldalakat pedig az A₁ és a B₁ pontokban. Tegyük fel, hogy az A₁B₁ egyenes az AB oldalt D-ben metszi. Bizonyítsuk be, hogy a DM egyenes merőleges a C-ből induló súlyvonalra. (5 pont)

Megoldás. Természetesen `oldal' alatt mindig a megfelelő oldal egyenesét értjük. Feltesszük továbbá, hogy a háromszög nem derékszögű, ellenkező esetben ugyanis vagy az M és D pontok, vagy az A₁ és B₁ pontok egybeesnek. Jelölje az M pontból az A, B, C, D pontokba mutató vektorokat rendre a, b, c, d. Jegyezzük meg, hogy a nem párhuzamos b-vel. Ekkor a c vektor felírható c=- $alpha$ a- $beta$ b alakban, ahol könnyen ellenőrizhető, hogy az $alpha$ , $beta$ számok egyike sem lehet 0 vagy -1, továbbá $alpha$ + $beta$ $ne$ -1. 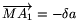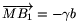Az $\overrightarrow{MA_1}=-\delta a$ , $\overrightarrow{MB_1}=-\gamma b$ jelöléssel élve a $gamma$ , $delta$ együtthatók könnyen meghatározhatók. Valóban, a b+ $delta$ a és b-c=(1+ $beta$ )b+ $alpha$ a vektorok párhuzamosságából $delta$ = $alpha$ /(1+ $beta$ ) adódik; ugyanígy $gamma$ = $beta$ /(1+ $alpha$ ). Könnyen meggyőződhetünk arról is, hogy $gamma$ és $delta$ sem lehet 0 vagy -1.

Mivel D az AB és A₁B₁ egyenesek metszéspontja, alkalmas s és t 1-től kölönböző számokkal d+ $delta$ a=t(d+ $gamma$ b) és d-a=s(d-b). Innen d kiküszöbölése után a

$delta$ (s-1)a+ $gamma$ t(1-s)b=(1-t)a+(t-1)sb

egyenlőséghez jutunk, ahonnan $delta$ (s-1)=1-t és $gamma$ t(1-s)=(t-1)s adódik, hiszen az a és b vektorok nem párhuzamosak. Innen s $ne$ 1 miatt $delta$ s= $gamma$ t, vagyis $delta$ (s-1)=1-( $delta$ / $gamma$ )s, ahonnan

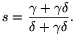
$s={\gamma+\gamma\delta\over\delta+\gamma\delta}.$

Ha az AB oldal felezőpontját F-fel jelöljük, akkor

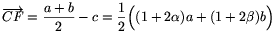
$\overrightarrow{CF}={{a}+{b}\over2}-{c}={1\over2}\Bigl((1+2\alpha){a}+(1+2\beta){b}\Bigr)$

és

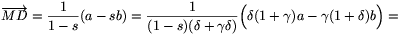
$\overrightarrow{MD}={1\over1-s}({a}-s{b})={1\over(1-s)(\delta+\gamma\delta)}\Bigl(\delta(1+\gamma){a}-\gamma(1+\delta){b}\Bigr)=$

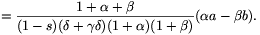
$={1+\alpha+\beta\over(1-s)(\delta+\gamma\delta)(1+\alpha)(1+\beta)}(\alpha a-\beta b).$

Elegendő tehát annyit belátni, hogy az $alpha$ a- $beta$ b vektor merőleges az (1+2 $alpha$ )a+(1+2 $beta$ )b vektorra, vagyis hogy ezen vektorok

p= $alpha$ (1+2 $alpha$ )a²- $beta$ (1+2 $beta$ )b²+( $alpha$ - $beta$ )ab

skaláris szorzata 0.

Mivel M az ABC háromszög magasságpontja, a(b-c)=b(a-c)=0. Ezért ac=ab=cb, ahonnan - $alpha$ a²- $beta$ ab=ab=- $alpha$ ab- $beta$ b², vagyis $alpha$ a²=-(1+ $beta$ )ab és $beta$ b²=-(1+ $alpha$ )ab. Innen

p=-(1+ $beta$ )(1+2 $alpha$ )ab+(1+ $alpha$ )(1+2 $beta$ )ab+( $alpha$ - $beta$ )ab=0,

ahogyan azt igazolni kívántuk.

B.3551. Legyenek az a, b, c, d olyan pozitív egészek, melyekre

a²+b²+ab=c²+d²+cd.

Bizonyítsuk be, hogy a+b+c+d összetett szám. (5 pont)

Megoldás. Tegyük fel, hogy a bizonyítandó állítással ellentétben a+b+c+d=p, ahol p $ge$ 4 prímszám. Ekkor az általánosság megszorítása nélkül feltehetjük, hogy a+b páros, míg c+d páratlan szám. Az a+b=2B, ab=A jelöléssel élve, a és b éppen az x²-(2B)x+A=0 egyenlet gyökei, melyek pontosan akkor esnek egybe, ha A-B²=0, ellenkező esetben pedig nyilván különböző maradékot adnak p-vel osztva.

Mivel c+d=p-2B, a

(2B)²-ab=a²+b²+ab=c²+d²+cd=(p-2B)²-cd=p(p-4B)+(2B)²-cd

összefüggésből látjuk, hogy cd ugyanolyan maradékot ad p-vel osztva, mint ab. Ezért

c²+(2B)c+A $equiv$ c²-(c+d)c+cd=0 (mod p),

és hasonlóképpen d²+(2B)d+A is osztható p-vel. Vagyis p osztója a (c+B)²+(A-B²) és (d+B)²+(A-B²) kifejezéseknek.

Tekintsük most A-t és B-t rögzítettnek, és vizsgáljuk meg, hogy az 1,2,...,p-1 számok között hány olyan y található, melyre (y+B)²+(A-B²) osztható p-vel. Ha A-B²=0, akkor szükségképpen (y+B)², és így y+B is osztható p-vel, ezért ekkor legfeljebb egy ilyen y szám lehet. Ha A-B² $ne$ 0, akkor is legfeljebb csak két ilyen szám lehet. Ha ugyanis y₁,y₂,y₃ is ilyenek, akkor i $ne$ j esetén

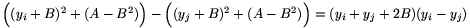
$\Bigl((y_i+B)^2+(A-B^2)\Bigr)-\Bigl((y_j+B)^2+(A-B^2)\Bigr)=(y_i+y_j+2B)(y_i-y_j)$

osztható p-vel, ahonnan |y_i-y_j|<p miatt adódik, hogy y_i+y_j+2B is osztható p-vel. Ezért (y₁+y₂+2B)-(y₁+y₃+2B)=y₂-y₃ is osztható p-vel, ami nem lehetséges, amint azt már az előbb láttuk.

Helyettesítsük most be a p-a és p-b számokat az (y+B)²+(A-B²) kifejezésbe.

(p-a+B)²+(A-B²)=p(p-2a+2B)+a²-(2B)a+A=p(p-2a+2B),

és hasonlóképpen kapjuk, hogy (p-b+B)²+(A-B²) is osztható p-vel. Az eddig elmondottak szerint tehát az A-B²=0 esetben szükségképpen c=d=p-a=p-b, egyébként pedig c és d közül az egyik (p-a)-val, a másik (p-b)-vel egyenlő. Mindkét esetben azt kapjuk, hogy a+b+c+d=2p. Ez az ellentmondás mutatja, hogy kiindulási feltevésünk nem lehet helyes, amivel a bizonyítandó állítást igazoltuk.

Már regisztráltál?
Új vendég vagy?