A 2002 májusi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 293. Mutassuk meg, hogy tetszőleges m $\displaystyle \ge$ 2 egészhez léteznek olyan a és b pozitív egészek, amelyek m-es számrendszerben felírt alakja együttesen minden számjegyből pontosan annyit tartalmaz, mint az a^.b szám m-es számrendszerbeli alakja.

Szobonya László, Budapest

1. megoldás (Zsbán Ambrus megoldása). Mint könnyen ellenőrizhető, m-es számrendszerben

11^.(m-1)10100(m-1)=1001110(m-1)(m-1).

2. megoldás (Kovács Erika Renáta megoldása).

11^.(m-1)101(m-2)01=10011(m-1)(m-2)11.

A. 294. Definiáljuk az a₁,a₂,... sorozatot a következő rekurzióval: a₁=1, $\displaystyle a_{n+1}={a_1a_n+a_2a_{n-1}+\dots+a_na_1\over n+1}$ . Igazoljuk, hogy a $\displaystyle b_n=\root{n}\of{a_n}$ sorozat konvergens.

Megoldás. A definícióból látható, hogy az (a_n) sorozat elemei a (0,1) intervallumba esnek.

Megmutatjuk, hogy a sorozat szigorúan monoton fogy. Az első elemekre ezt könnyű ellenőrizni: a₁=1, 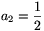$a_2={1\over2}$ , $\displaystyle a_3={1\over3}$ , $\displaystyle a_4={11\over48}$ . Legyen n $ge$ 4 és tegyük fel, hogy a₁<...<a_n. Ekkor

$\displaystyle (n+1)a_{n+1}=a_1a_n+\sum_{k=2}^na_ka_{n+1-k}<$

\(\displaystyle Ezután indukcióval azt is bebizonyítjuk, hogy a szomszédos elemek hányadosa, az $\displaystyle {a_{n+1}\over a_n}$ sorozat szigorúan monoton nő. (A bizonyítás Csóka Endre dolgozatából származik.) A monotonitást az első elemekre könnyen ellenőrizhetjük:

$\displaystyle {a_2\over a_1}={{1\over2}\over1}=0.5,\quad{a_3\over a_2}={{1\over3}\over{1\over2}}\approx0.667,\quad{a_4\over a_3}={{11\over48}\over{1\over3}}\approx0,688.$

Legyen tehát n $\displaystyle ge$ 3, és tegyük fel, hogy $\displaystyle {a_2\over a_1}<\dots<{a_{n+1}\over a_n}$ . Ebből bebizonyítjuk, hogy $\displaystyle {a_{n+1}\over a_n}<{a_{n+2}\over a_{n+1}}$ , azaz a_na_n+2-a_n+1²>0.

(n+2)(a_na_n+2-a_n+1²)=

=a_n^.(n+2)a_n+2-a_n+1^.(n+1)a_n+1-a_n+1²=

$\displaystyle =a_n\sum_{k=1}^{n+1}a_ka_{n+2-k}-a_{n+1}\sum_{k=1}^na_ka_{n+1-k}-a_{n+1}^2=$

$\displaystyle =\sum_{k=1}^na_k(a_na_{n+2-k}-a_{n+1}a_{n+1-k})+a_na_{n+1}-a_{n+1}^2.$

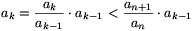Az utolsó összegben az első tag 0. Ha 2 $\displaystyle le$ k $\displaystyle le$ n, akkor az indukciós feltevés szerint $\displaystyle a_na_{n+2-k}-a_{n+1}a_{n+1-k}=a_na_{n+1-k}\left({a_{n+2-k}\over a_{n+1-k}}-{a_{n+1}\over a_n}\right)<0$ és $a_k={a_k\over a_{k-1}}\cdot a_{k-1}<{a_{n+1}\over a_n}\cdot a_{k-1}$ , ezért

(n+2)(a_na_n+2-a_n+1²)>

$\displaystyle$ {a_{n+1}\over a_n}\sum_{k=2}^na_{k-1}(a_na_{n+2-k}-a_{n+1}a_{n+1-k})+a_na_{n+1}-a_{n+1}^2=">

$\displaystyle =a_{n+1}\sum_{k=2}^na_{k-1}a_{n+2-k}-{a_{n+1}^2\over a_n}\sum_{k=2}^na_{k-1}a_{n+1-k}+a_na_{n+1}-a_{n+1}^2=$

$\displaystyle =a_{n+1}\big((n+1)a_{n+1}-a_na_1\big)-{a_{n+1}^2\over a_n}\cdot na_n+a_na_{n+1}-a_{n+1}^2=0.$

Ezzel a hányados sorozat monotonitását igazoltuk.

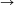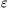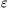Legyen $\displaystyle B=\lim{a_{n+1}\over a_n}$ . Ez a határéték létezik, mert a hányados sorozat monoton nő és felülről korlátos: az 1 egy felső korlátja. Bebizonyítjuk, hogy b_n $to$ B. Legyen 0< $\displaystyle varepsilon$ <1 tetszőleges valós szám; azt kell megmutatnunk. hogy elég nagy n esetén (1- $varepsilon$ )B<b_n<(1+ $varepsilon$ )B.

Mivel a₁=1 és minden n-re 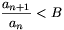${a_{n+1}\over a_n}<B$ , az is igaz, hogy a_n<B^n-1, amiből

$\displaystyle b_n=a_n^{1/n}<{1\over B^{1/n}}\cdot B.$

A B^1/n sorozat 1-hez tart, ezért elég nagy n esetén valóban $\displaystyle {1\over B^{1/n}}<1+\varepsilon$ .

A B szám definíciója szerint létezik egy olyan n₀ index, hogy n $\displaystyle ge$ n₀ esetén 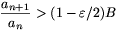${a_{n+1}\over a_n}>(1-\varepsilon/2)B$ . Ezért n>n₀ esetén

b_n=a_n^1/n>(a_n₀^.((1- $\displaystyle varepsilon$ /2)B)^n-n₀)^1/n=

$\displaystyle =\left({a_{n_0}\over\big((1-\varepsilon/2)B)^{n_0}}\right)^{1/n}\cdot(1-\varepsilon/2)B.$

Az utolsó kifejezés (1- $\displaystyle varepsilon$ /2)B-hez tart, ezért elég nagy n esetén nagyobb lesz, mint (1-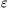 $varepsilon$ )B.

Ezzel bebizonyítottuk, hogy a b_n sorozat konvergens.

A. 295. Az x₁,x₂...,x_n pozitív számokra teljesül, hogy

$\displaystyle {1\over1+x_1}+{1\over1+x_2}+\dots+{1\over1+x_n}=1.$

Bizonyítsuk be, hogy

$\displaystyle \sqrt{x_1}+\sqrt{x_2}+\dots+\sqrt{x_n}\ge(n-1) \left({1\over\sqrt{x_1}}+{1\over\sqrt{x_2}}+\dots+ {1\over\sqrt{x_n}}\right).$

Vojtech Jarník Matematikaverseny, Ostrava, 2002

1. megoldás. A szimmetria miatt feltehetjük, hogy x₁ $\displaystyle le$ x₂ $\displaystyle le$ ... $\displaystyle le$ x_n.

Az (1) egyenlet alapján tetszőleges 1 $\displaystyle le$ i<j $\displaystyle le$ n indexekre 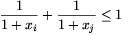${1\over1+x_i}+{1\over1+x_j}\le1$ . Ezt átrendezve kapjuk, hogy x_ix_j $ge$ 1.

Írjuk át a bizonyítandó állítást a következő alakba:

(2a)	$\displaystyle \left(\sqrt{x_1}+{1\over\sqrt{x_1}}\right)+\dots+\left(\sqrt{x_n}+{1\over\sqrt{x_n}}\right)\ge n\left({1\over\sqrt{x_1}}+{1\over\sqrt{x_2}}+\dots+{1\over\sqrt{x_n}}\right)$

Tekintsük az $\displaystyle y_i=\sqrt{x_i}+{1\over\sqrt{x_i}}$ (i=1,2,...,n) számokat. Megmutatjuk, hogy y₁ $le$ y₂ $\displaystyle le$ ... $\displaystyle le$ y_n. Ha ugyanis 1 $\displaystyle le$ i<j $\displaystyle le$ n, akkor az y_i $le$ y_j egyenlőtlenség a következőkkel ekvivalens:

$\displaystyle \sqrt{x_i}+{1\over\sqrt{x_i}}\le\sqrt{x_j}+{1\over\sqrt{x_j}};$

$\displaystyle \sqrt{x_j}(x_i+1)-\sqrt{x_i}(x_j+1)\le0;$

$\displaystyle \big(\sqrt{x_i}-\sqrt{x_j}\big)\big(\sqrt{x_ix_j}-1\big)\le0.$

Az $\displaystyle {1\over1+x_1}{1\over1+x_2}\dots,{1\over1+x_n}$ és y₁...,y_n sorozatok ellentétesek rendezettek, ezért a Csebisev-egyenlőtlenségből

$\displaystyle {{1\over1+x_1}+\dots+{1\over1+x_n}\over n}\cdot{y_1+y_2+\dots+y_n\over n}\ge{{y_1\over1+x_1}+\dots+{y_n\over1+x_n}\over n}.$

Ez átrendezve éppen (2a).

2. megoldás (Kovács Erika Renáta megoldása). Az 1. megoldáshoz hasonlóan kapjuk, hogy 1 $\displaystyle le$ i<j $\displaystyle le$ n esetén x_ix_j $ge$ 1.

Az (1) feltétellel ekvivalens, hogy

$\displaystyle {x_1\over1+x_1}+{x_2\over1+x_2}+\dots+{x_n\over1+x_n}=n-1.$

Ezért a bizonyítandó állítást a következő alakba is írhatjuk:

$\displaystyle \sum_{i=1}^n{1\over1+x_i}\sum_{j=1}^n\sqrt{x_j}\ge\sum_{i=1}^n{x_i\over1+x_i}\sum_{j=1}^n{1\over\sqrt{x_j}}.$

A két oldal különbsége:

$\displaystyle \sum_{i=1}^n{1\over1+x_i}\sum_{j=1}^n\sqrt{x_j}-\sum_{i=1}^n{x_i\over1+x_i}\sum_{j=1}^n{1\over\sqrt{x_j}}=$

$\displaystyle =\sum_{i=1}^n\sum_{j=1}^n\left({\sqrt{x_j}\over1+x_i}-{x_i/\sqrt{x_j}\over1+x_i}\right)=$

\(\displaystyle =\sum_{1\le i\(\displaystyle =\sum_{1\le i Az utolsó összegben mindegyik tag nemnegatív.

Már regisztráltál?
Új vendég vagy?