A 2002. májusi informatika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

I. 25. A Zeckendorf tétel alapján minden természetes szám egyértelműen előállítható Fibonacci számok összegeként úgy, hogy n =F_k1 + F_k2 + ...+ F_kr, ahol 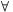i (1 \(\displaystyle \le\)i <r): k_i \(\displaystyle \ge\)k_i+1 + 2, és k_r \(\displaystyle \ge\)2. A Fibonacci számokat az alábbi módon számolhatjuk:

\(\displaystyle F_k=\cases{0{\rm\ ha\ }k=0\cr1{\rm\ ha\ }k=1\cr F_{k-1}+F_{k-2}{\rm\ ha\ }\)1.} ">

Készítsünk programot (I25.PAS,...), amely adott n (1 \(\displaystyle \le\)n \(\displaystyle \le\)10 000 000) természetes számot felbont Fibonacci számok összegére! (A megoldásban a hatékonyságot is értékeljük.) (10 pont)

Megoldás:

Két megoldást is adunk erre a feladatra. Először az első ötletet követjük, majd azt tesszük hatékonyabbá a számolási időt javítva a memóriafoglaltság rovására.

Eljárás Fibonacci_felbontas;
  Változók N,E,F:egész;

  Be: N;
  Ciklus amíg N>0

    E:=0;
    F:=1;
    Ciklus amíg F<=N
      S:=E;
      E:=F;
      F:=E+S;
//      F:=F+E;
//      E:=F-E;
    Ciklus vége

    Ki: E;
    N:=N-E;
  Ciklus vége
Eljárás vége.

A következő - hatékonyabb - megoldásban is az N számnál kisebb Fibonacci számok közül ki a legnagyobbat az összeg képzéséhez. Majd azt levonjuk az N-ből és folytatjuk a keresést. De itt nem számoljuk ki többször a sorozat minden elemét, hanem eltároljuk. Illetve felhasználjuk, hogy biztosan nem szerepel két egymást követő Fibonacci szám a felbontásban.

Eljárás Fibonacci_felbontas2;
  változók i,n,m,db: egész;
           f,k     : tömb(0..50:egész);

  Be: N;
  f[0]:=0; f[1]:=1;
  m:=2;
  Ciklus
    f[m]:=f[m-1]+f[m-2]; m:=m+1
  amíg f[m-1]<=n;
  ciklus vége

  m:=m-2;
  Ki: f[m];
  n:=n-f[m];
  db:=1; k[db]:=m;

  m:=m-2;
  Ciklus amíg n>0
    Ha f[m]>n akkor
      m:=m-1
    Különben

      Ki: '+',f[m]);
      n:=n-f[m];
      db:=db+1; k[db]:=m;
      m:=m-2;
    Elágazás vége;
  ciklus vége;

  Ki: 'F(',k[1],')';
  ciklus i:=2-től db-ig
    Ki: '+F(',k[i],')';
  ciklus vége;
eljárás vége.

I. 26. A Sierpinski csipke egy rekurzív ábra, ami úgy keletkezik, hogy első lépésben egy négyzet alakú terítőből kivágjuk a középső, harmad akkora oldalhosszúságú négyzetet. Ez a csipke 1. szintje. Az ezután maradt részt 8 kisebb négyzet alakú résznek véve, mindegyikre végrehajtjuk ugyanezt a műveletet. Ez lesz a 2. szint. Az eljárást a megmaradt 8^.8, kilenced akkora területtel folytatjuk tovább...

Készítsünk programot (I26.PAS,...), amely beolvassa a szint sorszámát, majd kirajzolja az adott szintű Sierpinski csipkét, szürkére színezve a megmaradt részeket!

1. szint	2. szint	3. szint	4. szint

(10 pont)

Megoldás:

Ennek a problémának egyszerű rekurzív megoldása található alább, ahol egy négyzettel úgy foglalkozunk, hogy a középső 1/3-szor 1/3-os (1/9) területét fehérre festjük, és a többi nyolc részre is elvégezzük ugyanezt az eljárást.

Eljárás Sierpinski;
  Változók N:Egész;
  Be: N;
  feherre_fest(0,0,480,480,N);
eljárás vége;

Eljárás feherre_fest(x1,y1,x2,y2,N:Egész);
  Ha N>0 akkor
    Színbeállítás(FEHÉR);
    NégyzetRajzolás(x1+(x2-x1)/3,y1+(y2-y1)/3,x2-(x2-x1)/3,y2-(y2-y1)/3));
    feherre_fest(x1,y1,x1+(x2-x1)/3,y1+(y2-y1)/3,N-1);
    feherre_fest(x1+(x2-x1)/3,y1,x2-(x2-x1)/3,y1+(y2-y1)/3,N-1);
    feherre_fest(x2-(x2-x1)/3,y1,x2,y1+(y2-y1)/3,N-1);
    feherre_fest(x1,y1+(y2-y1)/3,x1+(x2-x1)/3,y2-(y2-y1)/3,N-1);
    feherre_fest(x2-(x2-x1)/3,y1+(y2-y1)/3,x2,y2-(y2-y1)/3,N-1);
    feherre_fest(x1,y2-(y2-y1)/3,x1+(x2-x1)/3,y2,N-1);
    feherre_fest(x1+(x2-x1)/3,y2-(y2-y1)/3,x2-(x2-x1)/3,y2,N-1);
    feherre_fest(x2-(x2-x1)/3,y2-(y2-y1)/3,x2,y2,N-1);
  elágazás vége;
eljárás vége;

I. 27. A ,,Francia zászló'' probléma egy szabályozási feladat. Egymás mellett levő N darab, egyformán működő cellát olyan állapot-átmenet függvénnyel (cellába írandó képlettel) kell ellátni, aminek hatására az N cellában a francia zászló mintázata alakul ki: az első N/3 cella piros, a második N/3 cella fehér, a harmadik N/3 cella pedig kék színű lesz.

A kiinduló állapotban a bal szélső cellát impulzus éri, aminek hatására három hullám (i,j,k) indul ki belőle. Minden cellában 1 időegységig tartózkodik az i-hullám, majd továbblép a jobb oldali szomszédjába, a j-hullám 2, a k-hullám pedig 5 időegységig tartózkodik egy-egy cellában, mielőtt a következőbe jut. Az i-hullám a jobb szélső cellából visszaverődik és kiolt minden hullámot, amivel találkozik.

Ha egy cellát i-hullám ér, akkor az eredetileg szürke cella kék színű lesz, ha j-hullám éri, akkor fehér, ha pedig k-hullám, akkor piros. Ha a visszavert i-hullám ér egy cellához, akkor annak színe a továbbiakban nem változik. Az ábrákon az egyes lépéseknek az egyes sorok felelnek meg. (Az ábrák a lap hátsó borítóján találhatók.)

1. ábra	2. ábra	3. ábra

Ha a bal szélső cellát újabb impulzus éri, akkor újra elindítja az i-, j- és k-hullámot, s a mintázat újra kialakul (2. ábra). Ha pedig a cellasort szétszakítjuk (beszúrunk a táblázatba egy üres oszlopot), akkor a mintázat külön-külön mindkét részben kialakul. (3. ábra)

Készítsünk Excel állományt (I27.XLS) a ,,Francia zászló'' probléma megoldására. (10 pont)

Megoldás:

A feladatot három részfeladatra bontjuk. A Munka2 nevű lapon az átmeneteket írjuk fel, a Munka1 lapon pedig az állapotokat tároljuk számérték és szín megjelenítésével..
A Munka2 lapon B10-es cellába egyet, míg a mellette levőkbe az AG oszlopig 0-át írunk, majd az alábbi képletnek megfelelően töltjük ki a következő sorokat (mondjuk 100-ig).

C15=HA(B15="";
 HA(VAGY(C14=1;C13=1);
  2;
  HA(VAGY(C14=2;C13=2;C12=2;C11=2;C10=2);
   3;
   0
  )
 );
 HA(B14=1;
  HA(D14="";4;1);
  HA(VAGY(C14=4;D14=4);
   HA(C14=1;0;4);
   HA(B13=2;
    2;
	HA(ÉS(B10=3;C14<>1;C13<>1;C12<>1;C11<>1;C10<>1);
	 3;
	 0)
	)
  )
 )
)

Átírva:

ha B15=""
  akkor
    ha C14=1 vagy C13=1
      akkor
        2
      különben
        ha C14=2 vagy C13=2 vagy C12=2 vagy C11=2 vagy C10=2
          akkor
            3
          különben
            0
        elágazás vége
    elágazás vége
  különben
    ha B14=1
      akkor
        ha D14=""
          akkor
            4
          különben
            1
        elágazás vége
      különben
        ha C14=4 vagy D14=4
          akkor
            ha C14=1
              akkor
                0
              különben
                4
            elágazás vége
          különben
            ha B13=2
              akkor
                2
              különben
                ha B10=3 és C14<>1 és C13<>1 és C12<>1 és C11<>1 és C10<>1
                  akkor
                    3
                  különben
                    0
                elágazás vége
            elágazás vége
        elágazás vége
    elágazás vége
elágazás vége

B10=HA(Munka2!B10=1;1;B9)

A többi cella ebben a sorban (AG-ig) kilences (9) értéket kap.
A többi cella az alábbi képlet szerint kap értéket.

C15=HA(Munka2!C15=1;1;HA(Munka2!C15=2;2;HA(Munka2!C15=3;3;C14)))

Vagyis ha az átmenet egyes (1), akkor itt is egyes (1) az érték, ugyanígy, ha kettes (2), akkor kettes (2), ha pedig hármas (3), akkor hármas (3). Minden más esetben az előző állapot marad, vagyis a felette levő értéket kapja meg.
A B110-es cellától az AG200-asig a cellákat feltételesen formázzuk úgy, hogy a neki megfelelő 100 sorral feljebb található cella tartalmától függően legyen a cellának kék, fehér vagy piros színe. Elég megformáznunk egy cellát, majd annak az átmásolásával ez a (feltételes formázás) tulajdonság is továbbítódik.

Például az S142 mezőt a következő képen formázzuk: