A 2002. szeptemberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3562. Egy nyolcéves kislány konvex hétszög alapú tortát kapott a születésnapjára. A tortát a hétszög átlói mentén függőleges vágásokkal szeletelték föl. Az ünnepelt nyolcszög alapú szeletet szeretne kapni. Teljesülhet-e a kívánsága? (3 pont)

Megoldás: Képzeljünk el egy tortaszeletet. Ennek alapja egy olyan konvex sokszög, melyet a hétszög néhány átlója határol. Ezek között a hétszög egy adott csúcsából kiinduló átlók közül legfeljebb kettő szerepelhet, ami legfeljebb 14 átlót jelent. Igenám, de ezeket az átlókat mindkét végpontjuknál számításba vettük, vagyis a szóban forgó sokszöget a hétszög átlói közül legfeljebb 7 darab határolhatja, a tortaszelet alapja nem lehet nyolcszög.

B.3563. Legalább mekkora t érték esetén teljesül minden nemnegatív x, y valós számra a $\displaystyle \sqrt{xy}\leq t(2x+3y)$ egyenlőtlenség? (3 pont)

Megoldás: A számtani és mértani közepek közötti egyenlőtlenség alapján

$\displaystyle t(2x+3y)={2t}{2x+3y\over2}\ge{2t}\sqrt{6xy}\ge{2t\sqrt{6}}\sqrt{xy}\ge\sqrt{xy},$

valahányszor $\displaystyle t\ge1/(2\sqrt{6})$. Ennél kisebb t értékek azonban nem jöhetnek szóba, hiszen 2x=3y>0 esetén

$\displaystyle \sqrt{xy}={1\over2\sqrt{6}}(2x+3y$t(2x+3y),">

valahányszor $\displaystyle t<1/(2\sqrt{6})$. A keresett érték tehát $\displaystyle 1/(2\sqrt{6})$.

B.3564. Vigyük át az (x,y) koordináta-sík A(0;1) pontját a B(3;2) pontba az x-tengelyre való tükrözések és az A pont körüli elforgatások alkalmazásával. (4 pont)

Megoldás: Az A pontot az x-tengelyre tükrözve kapjuk az A₁(0,-1) pontot. Ezt az A pont körül elforgatva, a következő pont, amit A₂-vel jelölünk, az A középpontú, AA₁=2 sugarú körön lesz. Az A₂ pont x-tengelyre vonatkozó A₃ tükörképe tehát az A₁ középpontú, 2 sugarú körön lesz, melynek egyenlete x²+(y+1)²=4. Képzeljük el, hogy az A₃ pontot A körül alkalmasan elforgatva már megkaphatjuk a B pontot. Ez azt jelenti, hogy A₃ rajta van az A középpontú, $\displaystyle AB=\sqrt{10}$ sugarú körön is, melynek egyenlete x²+(y-1)²=10. A két egyenletet egymásból kivonva x kiküszöbölhető, y=-3/2 adódik, ami pontosan $\displaystyle x=\pm\sqrt{15}/2$ esetén elégíti ki mindkét egyenletet. Innen leolvashatjuk, hogy egy lehetséges megoldás a következő, 4 lépésből álló eljárás:

$\displaystyle A(0,1)\longrightarrow A_1(0,-1)\longrightarrow A_2(\sqrt{15}/2,3/2)\longrightarrow A_3(\sqrt{15}/2,-3/2)\longrightarrow B(3,2).$

B.3565. Adott 2002 doboz, mindegyikükben néhány kavics. Ezen kívül korlátlan számú kavics áll rendelkezésünkre. Egy lépésben bármely k dobozba betehetünk 1-1 kavicsot. Elérhető-e, hogy bizonyos számú lépés után minden egyes dobozban ugyanannyi kavics legyen, ha

a) k=8

b) k=9? (4 pont)

Megoldás: Ha k=8, akkor a feladat nem mindig oldható meg. Ha ugyanis kezdetben a dobozok együttesen páratlan sok kavicsot tartalmaznak, akkor ez a tulajdonság minden egyes lépés után megmarad. Ha néhány lépés után minden egyes dobozban ugyanannyi kavics lenne, akkor a dobozokban lévő kavicsok együttes száma 2002 többszöröse, vagyis páros szám lenne, ami esetünkben nem lehetséges.

Ha azonban k=9, akkor a feladat mindig megoldható. Jelölje kezdetben a legtöbb kavicsot tartalmazó dobozban lévő kavicsok számát K, az összes dobozban lévő kavicsok együttes számát pedig M. A K,K+1,...,K+8 számok között van egy olyan, jelöljük ezt L-lel, amelyre 2002L ugyanolyan maradékot ad 9-cel osztva, mint M. Valóban, a 2002K,2002(K+1),...,2002(K+8) számok mind különböző maradékot adnak 9-cel osztva (ellenkező esetben ugyanis az azonos maradékot adók különbsége, 2002t, ahol 1$\displaystyle le$t$\displaystyle le$8, osztható lenne 9-cel, ami nem lehetséges, hiszen 2002 nem osztható 3-mal), és mivel itt 9 számról van szó, megkapjuk mind a 9 lehetséges maradékot. Nem nehéz megadni egy olyan eljárást, amelynek végén minden dobozban pontosan L kavics lesz. Valóban, ameddig a dobozokban összesen legfeljebb 2002K-9 kavics van, és minden dobozban legfeljebb K kavics van, addig a soron következő lépésben a 9 kavicsot el tudjuk úgy helyezni, hogy minden dobozban továbbra is legfeljebb K darab kavics legyen. Az utolsó lehetséges ilyen lépés után minden egyes dobozban legfeljebb K kavics van, a dobozokban lévő összes kavics együttes száma pedig 2002K-8 és 2002K között van, és ugyanolyan maradákot ad 9-cel osztva, mint M, vagyis mint 2002L. Ha L=K, akkor már készen is vagyunk, ellenkező esetben pedig úgy járunk el, hogy minden egyes lépés után igaz legyen, hogy mindegyik dobozban vagy J vagy J+1 kavics van valamilyen K$\displaystyle le$J<L számra. Ez nyilván megtehető, egészen addig, amíg a dobozokban lévő kavicsok együttes száma a 2002L-9 értéket meg nem haladja. Ha már nem tudunk így tovább lépni, akkor a kavicsok együttes száma nyilván 2002L-8 és 2002L közé esik. Mivel 9-cel osztva ugyanolyan maradékot ad, mint 2002L, csakis 2002L lehet, és mivel ekkor minden egyes dobozban J vagy J+1 kavics van, ez csak úgy lehet, ha J=L-1, és minden dobozban éppen J+1=L kavics van.

B.3566. Az ABC háromszögről tudjuk, hogy minden P belső pontjára a PA, PB és PC szakaszokból háromszög szerkeszthető. Mutassuk meg, hogy az ABC háromszög szabályos. (4 pont)

Megoldás: Tegyük fel, hogy az állítással ellentétben a háromszög nem szabályos, ekkor van két különböző hosszúságú oldala. Az általánosság megszorítása nélkül feltehetjük, hogy a=BC<AC=b. Legyen b-a=$\displaystyle varepsilon$, P pedig olyan pont a háromszög belsejében, melynek a C csúcstól való távolsága, PC=$\displaystyle delta$ $le$ $varepsilon$ /3. A BCP háromszögre felírva a háromszög-egyenlőtlenséget kapjuk, hogy PB<PC+CB=a+ $delta$ . Hasonlóképpen az ACP háromszögből kapjuk, hogy AC<AP+PC, vagyis PA>AC-CP=b- $delta$ . Ekkor azonban

PA-PB>(b- $delta$ )-(a+ $delta$ )= $varepsilon$ -2 $delta$ $ge$ $delta$ =PC,

tehát PA>PB+PC, és ezért a PA,PB,PC szakaszokból nem szerkeszthető háromszög. Ez az ellentmondás igazolja a feladat állítását.

B.3567. Egy konvex ötszögről tudjuk, hogy minden oldala párhuzamos valamelyik átlójával. Mekkora lehet egy oldal és a vele párhuzamos átló hosszának aránya? (5 pont)

Megoldás: Jelölje az ötszög csúcsait valamely körüljárás szerint sorban A,B,C,D,E. Jelölje továbbá M és N az EC átlónak az AD illetve BD átlókkal való metszéspontját. Ekkor nyilván az ABCM és ABNE négyszögek paralelogrammák. Az AB=a,BC=b,DM=x,EM=y jelöléseket is bevezetve adódik, hogy AM=b, EN=MC=a, és így MN=t=a-y. Az AMC és DME háromszögek hasonlóságából kapjuk, hogy x:b=y:a, az AME és DMN háromszögek hasonlóságából pedig x:b=t:y. A két egyenlőséget összevetve kapjuk, hogy y²=at=a(a-y), vagyis y²+ay-a²=0, ahonnan 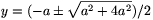$y=(-a\pm\sqrt{a^2+4a^2})/2$ . Mivel y>0, az AB oldal és a vele párhuzamos EC átló arányára

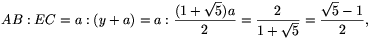
${AB:EC}={a:(y+a)}=a:{(1+\sqrt{5})a\over2}={2\over1+\sqrt{5}}={\sqrt{5}-1\over2},$

és nyilván ugyanez az aránya bármelyik oldal és az azzal párhuzamos átló hosszának.

B.3568. Mely $alpha$ szögetre igaz, hogy minden k nemnegatív egészre cos2^k $alpha$ $le$ 0? (5 pont)

Megoldás: Keressük az $alpha$ szöget $alpha$ =2 $pi$ x alakban, és képzeljük el x értékét négyes számrendszerben, `negyedes' törtként felírva. Ez nem lehet egy véges negyedes tört, hiszen ha x ilyen felírásában a negyedes vesszőt csak j darab számjegy követi, akkor 4^jx egész szám, és így cos2^2j $alpha$ =1>0. Ezért x egy olyan végtelen negyedes tört, melyben a negyedes vessző után egyes vagy kettes számjegy áll. Ha tekintjük a 4x,4²x,..., számokat, ezek olyan végtelen negyedes törtek, melyeket x-ből úgy nyerünk, hogy a negyedes vesszőt mindig egy hellyel jobbra tesszük. Lévén 2²ⁱ $alpha$ =2 $pi$ (4ⁱx), az előző gondolatmenet mutatja, hogy x végtelen negyedes tört alakjában a negyedes vessző után minden egyes számjegy 1 vagy 2. Mivel pedig 2 $alpha$ =2 $pi$ (2x), és a $beta$ =2 $alpha$ szögre is igaz, hogy minden k nemnegatív egész esetén cos2^k $beta$ $le$ 0, a 2x végtelen negyedes tört alakjára is igaz, hogy a negyedes vessző után minden egyes számjegy 1 vagy 2.

Vegyük észre azt, hogy ha x-ben a negyedes vessző utáni j-edik számjegy 1, a (j+1)-edik pedig 2, akkor 2x-ben a negyedes vessző utáni j-edik számjegy 3 lesz. Ha pedig x-ben a negyedes vessző utáni j-edik számjegy 2, a (j+1)-edik pedig 1, akkor 2x-ben a negyedes vessző utáni j-edik számjegy 0 lesz. Ezért szükségképpen x-ben a negyedes vessző után vagy minden egyes számjegy 1, vagy minden egyes számjegy 2. Ennek alapján x törtrésze vagy 1/3, vagy pedig 2/3. Könnyen ellenőrizhetjük, hogy mindkét esetben igaz, hogy minden k nemnegatív egészre 2^kx törtrésze is 1/3 vagy 2/3. Ezért a feltételnek eleget tevő $alpha$ szögek éppen a 2n $pi$ $pm$ 2 $pi$ /3 alakban felírható szögek, ahol n egész szám, amikor is minden k nemnegatív egészre cos2^k $alpha$ =-1/2.

B.3569. 100 kockáról tudjuk, hogy bármelyik kettőnek van közös belső pontja, és a kockák élei három adott egyenes valamelyikével párhuzamosak. Mutassuk meg, hogy ekkor az összes kockának van közös pontja.

Adjunk meg 100 kockát úgy, hogy közülük bármely háromnak legyen közös belső pontja, de ne legyen olyan pont, amelyik mindegyik kockában benne van. (5 pont)

Megoldás. Kockák helyett általánosabban téglatestekre bizonyíthatunk. A három adott egyenesnek megfelelően beszélünk majd ,,előre--hátra'', ,,jobbra--balra'' és ,,fel--le'' irányokról. Tekintsük a téglatestek közül azt, amelyiknek a felső lapja (F) a legmélyebben helyezkedik el; ekkor mindegyik téglatest alsó lapja F alatt van -- közülük a legfelsőt jelölje A. Hasonlóan, jobbra haladva legyen a bal oldali lapok közül a jobb szélen elhelyezkedő B, a jobb oldali (B-től szükségképpen jobbra eső) lapok közül a bal szélen lévő J. Végül jelölje a legelőrébb eső hátsó lapot H, a leghátrább található első lapot pedig E. Ekkor az F, A, B, J, H és E lapok síkjai olyan (nemüres) téglatestet határoznak meg, amely valamennyi téglatestnek része.

Rátérve a feladat második részére, tekintsünk először egy T tetraédert és állítsunk minden lapjára kifelé egy-egy olyan nagy kockát, hogy annak a tetraéderre fekvő lapja belsejében tartalmazza a tetraéder három csúcsát. Nem nehéz meggyőződni arról, hogy a négy kocka közül bármely háromnak van közös belső pontja, mind a négynek azonban nincs. Ezek után valamelyik kockát 97 példányban tekintve, a kívánt tulajdonsággal rendelkező 100 kockához jutunk.

B.3570. A folytonos f függvényre teljesül, hogy f(1000)=999 és f(x)^.f(f(x))=1 minden valós x számra. Határozzuk meg f(500) értékét. (4 pont)

Megoldás: f(x)^.f(f(x))=1

úgy is átírható, hogy ha y=f(x) valamely x-re, akkor f(y)=1/y (y $ne$ 0). f(1000)=999

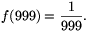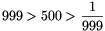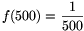, így $f(999)={1\over999}.$ Egy folytonos függvény két értéke között mindent felvesz, így $999>500>{1\over999}$ miatt van olyan x, melyre f(x)=500, azaz $f(500)={1\over500}$ .

Van a feladatnak megfelelő függvény: 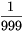${1\over999}$ és 999 között 1/x legyen a függvény, f(1000)=999 és más x-re 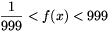${1\over999}<f(x)<999$ . Ez valóban kielégíti a feladat feltételeit.

B.3571. Egy egyenes csonkakúp alakú poharat körbegurítottunk egy kör alakú asztalon úgy, hogy mozgás közben sosem érte el az asztal peremét. Az asztal átmérője 1,6 m. A pohár alja 5 cm, a teteje pedig 6,5 cm átmérőjü kör. Milyen magas lehet a pohár? (4 pont)

Megoldás: Legyen a pohár magassága h, alkotója pedig $ell$ cm. Mivel a poharat határoló két körlap sugarának különbsége (6,5-5)/2=3/4 cm, Pithagorasz tétele alapján $ell$ ²=h²+(3/4)². Egészítsük ki a poharat gondolatban egy kúppá, melynek csúcsa a pohár tetejétől R cm-re van, ekkor a párhuzamos szelők tétele alapján R:6,5=(R- $ell$ ):5, ahonnan $ell$ =3R/13. Miközben a pohár körbegurul az asztalon, képzeletbeli kúpunk is ugyanezt teszi úgy, hogy mozgás közben csúcspontja egy helyben marad, a pohár tetejének az asztal lapjával érintkező pontja pedig egy R sugarú körvonalat ír le. Ez azért van így, mert ha a kúpot egy alkotója mentén felvágjuk, annak palástja a síkba kiteríthető, hiszen egy adott középponti szögű körív hossza egyenesen arányos a körív sugarával. A poharat tehát pontosan akkor lehet körbegurítani úgy az asztalon, hogy mozgás közben soha sem érje el az asztal peremét, ha a kúp R alkotója rövidebb az asztal sugaránál, vagyis ha R<80, $ell$ <240/13,

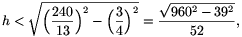
$h<\sqrt{\Bigl({240\over13}\Bigr)^2-\Bigl({3\over4}\Bigr)^2}={\sqrt{960^2-39^2}\over52},$

vagyis ha a kúp magassága $approx$ 18,45 cm-nél kevesebb.

Már regisztráltál?
Új vendég vagy?