 |
A 2002. szeptemberi C-jelű matematika gyakorlatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
C. 680. Egy kilenctagú választó testület három jelölt közül választ. Mindegyikük rangsorolja őket, az elsőnek 3, a másodiknak 2, a harmadiknak pedig 1 pontot ad. Összesítve a jelöltek pontszámát kiderült, hogy a sorrend egyértelmü, hármuk pontszáma különböző. A testület egyik tagja észrevette, hogy ha a választást úgy bonyolították volna le, hogy mind a kilencen csak egy jelöltet választanak ki és annak adnak 1 pontot, akkor a jelöltek sorrendje megfordulna. Hány pontot kaptak eredetileg a jelöltek?
Megoldás.A választó testület összesen 54 pontot adott a jelöltekre. Mivel a sorrend egyértelmű, és fordított eredményt hozott volna, ha csak az első helyen választottnak adnak egy pontot, ezért az első helyek alakulására csak a következő három eset lehetséges:
|
A-nak van: 2 első, 6 második és 1 harmadik helye, ez 19 pont.
B-nek van: 3 első, 3 második és 3 harmadik helye, ez 18 pont.
C-nek van: 4 első, 0 második és 5 harmadik helye, ez 17 pont.
C. 681. Az ábrán látható három emeletes ,,piramist'' 1 cm3-es kockákból építettük, felszíne 42 cm2. Ennek mintájára készítettünk egy nagyobb ,,piramist'' is, amelynek 2352 cm2 a felszíne. Hány emeletes?
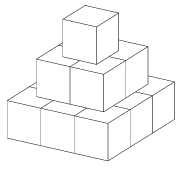
Megoldás. Jelöljük n-nel az emeletek számát. Ekkor a ,,piramis'' alulról és felülről is n2 cm2, továbbá minden oldalról (1+2+...+n), vagyis \(\displaystyle {n(n+1)\over2}\) cm2. Vagyis a felszíne: \(\displaystyle 2n^2+4\cdot{n(n+1)\over2}=2352\), amit 2n2+n-1176=0 alakra tudunk rendezni. Csak az egyik gyök pozitív: x=24. Így a ,,piramis'' 24 emeletes.
C. 682. A 2002-es adóbevallásnál azoknak, akiknek az éves bruttó jövedelme 1 050 000 forintnál több volt, a többlet 40%-án kívül 267 000 forintot kellett adóként befizetni. Mekkora havi bruttó jövedelem esetén lett a jövedelem 30%-a az adó?
Fried Ervin, Budapest
Megoldás. Legyen az éves bruttó jövedelem 1050000+x Ft. Ekkor a feladat szövege szerint: 267000+0,4x=(1050000+x).0,3. Ebből x=480000. Vagyis 1530000 Ft-os éves bruttó jövedelem esetén lesz az adó a jövedelem 30 %-a. Ez 127500 Ft-os havi bruttó jövedelmet jelent.
C. 683. Az ABC egyenlő szárú derékszögü háromszögben AC=BC. Az A csúcsból induló szögfelező a BC befogót a P pontban metszi. Igazoljuk, hogy a PB szakasz hossza egyenlő az ABC háromszög beírt körének átmérőjével.
Megoldás.
A befogók hossza legyen 1, az átfogó ekkor \(\displaystyle \sqrt2\). Tudjuk, hogy AF=BF=AE=1-r, továbbá AF+FB=AB, vagyis \(\displaystyle 2(1-r)=\sqrt2\), amiből \(\displaystyle r={2-\sqrt2\over2}\). Az AEK és az ACP háromszögek hasonlóságából: \(\displaystyle CP={r\over1-r}\), így \(\displaystyle PB=1-{r\over1-r}\). Az r-re kapott értéket ebbe behelyettesítve és átalakítva azt kapjuk, hogy \(\displaystyle PB=2-\sqrt2\), ami valóban 2r, vagyis a beírt kör átmérőjének a hossza.
C. 684. Oldjuk meg az
x-xy+y=1
x2+y2=17
egyenletrendszert.
Megoldás. Az első egyenletet rendezzük 0-ra és alakítsuk szorzattá: 0=xy-x-y+1=x(y-1)-(y-1)=(x-1)(y-1). Két eset van. Ha x=1, akkor a második egyenletből kapjuk az y-t. Ha y=1, akkor a második egyenletből kapjuk az x-et. A megoldások:
|