A 2002. szeptemberi számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3541. Egy vízzel félig töltött edényben egy vékony falú, zárt üveggömb úszik. Az asztalon áll még két azonos méretü pohár is, teletöltve vízzel. Ha az egyik pohár tartalmát beleöntjük az edénybe, azt tapasztaljuk, hogy az üveggömb jobban bemerül, ha a másik pohár vizet öntjük az edénybe, az üveggömb kevésbé merül be a vízbe. Hogyan lehetséges ez? (3 pont)

Frank János verseny, Szeged

Megoldás. Valami miatt más a másik két pohárban lévő víz sűrűsége (ez lehet például attól, hogy más a hőmérsékletük, esetleg attól, hogy különböző anyagokat oldottunk fel bennük).

P. 3542. Az ábrán látható oldalcsöves edény, valamint víz és mérőhenger felhasználásával hogyan becsülhetjük meg egy adott kémcső tömegét?

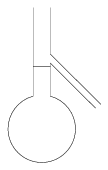
(3 pont)

Becslési verseny, Sárospatak

Megoldás. Az oldalcsöves edényt feltöltjük vízzel ameddig lehet, ezután beleengedjük a kémcsövet, és megmérjuk az oldalt kifolyó víz térfogatát. Ahány milliliter a víz térfogata, annyi gramm a kémcső tömege.

P. 3543. Éva, a 176 cm magas manöken a falra akasztott tükörben nézi magát. A tükör függőleges, magassága 75 cm. Éva egyenesen áll, és a szeme a talaj fölött 168 cm magasan van. Láthatja-e a saját szemét, ha még éppen látja a cipőjét? (3 pont)

Tarján Imre verseny, Szolnok

Megoldás. Ha Éva éppen látja a cipője orrát, akkor a tükör alja pont Éva szemmagasságának a felénél, tehát 84 cm magasan van. A tükör teteje tehát 159 cm magasan van a föld felett, így Éva nem látja a saját szemét a tükörben.

P. 3544. Az ábrán látható edényből kiszivattyúzták a levegőt. A felső gömbben víz van. Ha az alsó gömböt cseppfolyós nitrogénnel hütik, akkor a felső gömbben levő víz egy idő után megfagy. Mivel magyarázható a jelenség? Lehetséges-e, hogy a víz forrás közben fagy meg?

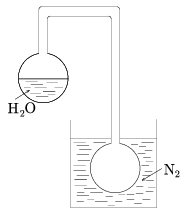
(4 pont)

Bródy Imre verseny, Ajka

Megoldás. Az alsó tartályban a nagyon alacsony hőmérséklet miatt a vízgőz lecsapódik és kifagy, a fölső tartályban ezért a víz folyamatosan párolog (forr is), és lehűl. A víz párolgáshője 100 és 0 ^oC között 2256 és 2500 kJ/kg között változik, a fajhője pedig 4,18 kJ/(kg^oC), ezért a mindenkori vízmennyiség nem egész 0,2%-ának az elpárolgása a maradék hőmérsékletét 1^oC-kal csökkenti. Ha tehát a felső edény elég jó hőszigetelő, a víz a felső tartályban előbb-utóbb 0^oC-ra hűl. A víz fagyáshője 333,7 kJ/kg, így a 0^oC-os víz kb. 12%-ának elpárolgása annyi hőt von el, amennyi a maradék fagyáshője, azaz elég jó hőszigetelés esetén a felső tartályban a víz - forrás közben - megfagy.

P. 3545. Két egyforma nagy, gömb alakú, vízzel telt üveg akvárium áll szorosan egymás mellett az asztalon. Mindkét akvárium középpontjában egy-egy kis hal úszik. Mekkorának, és milyen távolságban látják egymást a halacskák? A víz törésmutatója 1,33. (5 pont)

Holló András verseny, Jászberény

Megoldás. Jelölje a gömbök sugarát R, a víz törésmutatóját n. A két akvárium a közte lévő levegővel olyan, mintha egy mindkét oldalán R sugarú, homorú, levegővel telt lencse merülne vízbe. Ennek a (gyüjtő!)lencsének a fókusztávolsága

\(\displaystyle f={n\over{n-1}}{R\over2}\approx2R,\)

így a lencsétől (1/2)f távolságra lévő halak a lencsén át nézve a lencsétől f távolságra látszanak. A halacskák képe virtuális, egyenes állású, nagyságuk a halak méretének kétszerese, de mivel másfélszer távolabb jön létre, mint a halak tényleges távolsága, a szögnagyítás - ahányszor nagyobbnak látják egymást a halak - csak 4/3.

P. 3546. Az ürben egymástól 20 m távolságra lebeg egy 1000 kg-os ürhajó, benne egy 100 kg-os asztronauta, és egy 100 kg-os mühold. Az ürhajóról az asztronauta úgy rugaszkodik el -- megigazítani egy antennaelemet a müholdon --, hogy a sebessége az ürhajóhoz képest 1,1 m/s. A munkát 130 másodperc alatt végzi el, utána 100 másodperc alatt szeretne visszatérni az ürhajóhoz. A müholdhoz képest mekkora sebességgel kell elrugaszkodnia, hogy terve sikerüljön? (4 pont)

Öveges József emlékverseny, Tata

Megoldás. Írjuk le a mozgást abban a koordináta-rendszerben, amelyben az űrhajó kezdetben nyugalomban volt, és az időt mérjük az elrugaszkodás pillanatától. Az űrhajós sebessége az elrugaszkodás után 1/10-e lesz az űrállomásénak (a tömegarányok és a lendületmegmaradás törvénye miatt miatt), tehát az űrhajós sebessége 1 m/s, az űrállomásé pedig -0,1 m/s.

Az űrhajós a 20. másodpercben éri el a műholdat, majd a szerelési munkák idejére össze kell kapcsolódjon azzal, sebessége tehát (ismét a lendületmegmaradás miatt) 0,5 m/s-ra csökken. 130 másodperc alatt 65 méter utat tesz meg, a kiindulási helyétől tehát 85 méter távol lesz.

Ha 100 másodperc alatt szeretne visszaérni az űrállomáshoz, akkor a 250. másodpercben fognak találkozni, a kiindulási helytől 25 m távolságban. Az űrhajósnak tehát 100 másodperc alatt 85+25=110 méter utat kell megtennie, sebessége eszerint 1,1 m/s. Az űrhajós sebessége a második elrugaszkodás során 1,1-(0,5)=1,6 m/s-t változott, (ugyanennyit változott a műholdé is, hiszen a tömegük egyforma nagy), a műholdhoz viszonyított sebessége tehát 3,2 m/s kell legyen.

P. 3547. A geostacionárius müholdakat a következő módon állítják pályára: a mühold először a Földhöz közeli parkolópályán mozog, majd a hajtómüveit rövid ideig bekapcsolva olyan ellipszispályára állítják, amelynek földközel-pontja a parkolópályán, földtávol-pontja pedig a geostacionárius pályán van. Ezt elérve, a hajtómüveket újra müködésbe hozva körpályára állítják a müholdat.

Tegyük fel, hogy a parkolópálya a Föld felszínétől 200 km-re levő körpálya. Mennyi idő alatt ér innen a mühold a geostacionárius pálya magasságába? (5 pont)

Zemplén Győző verseny, Nagykanizsa

Megoldás. Ha a parkolópálya sugara r, a geostacionáriusé pedig R, akkor Kepler 3. törvénye szerint az átszállópályához tartozó T keringési idő

\(\displaystyle T=T_0\left(\frac{r+R}{2R} \right)^{3/2},\)

ahol a T₀ a geostacionárius pályához tartozó keringési idő, vagyis éppen 1 nap. A Föld egyenlítői sugara 6380 km, a geostacionárius pálya magassága az Egyenlítő fölött 35 680 km, így r=6580 km és R=42 060 km. Innen T=0,44 nap, azaz az átszállás ideje 0,22 nap=5,3 óra.

P. 3548. Az ábrán látható elektromos hálózatban a fogyasztók ellenállása R₁=300 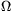, illetve R₂=700 \(\displaystyle Omega\). Az áramforrás elektromotoros ereje U₀=50 V, belső ellenállása elhanyagolható. A kondenzátor kapacitása C=50 F. A voltmérőt az A és B pontok közé kapcsolva azt tapasztaljuk, hogy U₁=14,5 V feszültséget mutat.

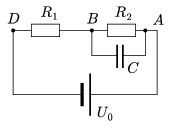
a) Mekkora a voltmérő ellenállása? Hány elektron távozik a kondenzátor negatív fegyverzetéről a feszültségmérés ideje alatt?

b) Mit mutat a voltmérő, ha a B és D pontok közé kapcsoljuk? Mekkora e mérés abszolút, illetve relatív hibája?

c) Legalább mekkora legyen egy voltmérő ellenállása, hogy a B és D pontok közé kapcsolva a mérés relatív hibája 1% legyen? (5 pont)

Vermes Miklós feladata nyomán

Megoldás. Ideális voltmérővel mérve a 300 ohmos ellenálláson 15 V, a 700 ohmos ellenálláson pedig 35 V mérhető. Ezekből a számokból sejthető, hogy a feladat kitűzési szövegében felcserélődött R₁ és R₂ számértéke: helyesen R₂=300 \(\displaystyle \Omega\) és R₁=700 \(\displaystyle \Omega\). Az alábbi végeredmények ezekre az adatokra érvényesek (de a hibás adatokkal helyesen kiszámolt megoldás is teljes pontszámot kapott).

a) R_b=6,1 k\(\displaystyle \Omega\), és n=1,6^.10¹⁴ elektron távozik a negatív fegyverzetről a mérés során. (A hibás adatokkal R_b=0,15 k\(\displaystyle \Omega\), és n=6,4^.10¹⁵ adódna.)

b) U_DB mért értéke 33,8 V, az abszolút hiba 1,2 V, ez a 35 V-nak 3,4%-a. (A hibás adatokkal U_DB mért értéke 6,2 V, az abszolút hiba 8,8 V, ez a 15 V-nak kb. 60%-a! A mérendő mennyiség ilyen durva megváltoztatása már nem is tekinthető ,,fizikai mérésnek'', hanem inkább ,,zárlatnak''.) c) \(\displaystyle R_b^{\prime}\approx20~{\rm k}\Omega\). (Érdekes, hogy az ellenállásokat felcserélve, vagyis a hibás adatokkal számolva ugyanekkora értéket kapunk.)

P. 3549. Egy optikai rácsot 589 nm hullámhosszúságú párhuzamos fénynyalábbal világítunk meg. A rácstól 3 méterre lévő ernyőn a nulladrendü és az elsőrendü elhajlási maximum egymástól 20 cm-re látható.

a) Centiméterenként hány karcolat van a rácson?

b) Milyen messze van a másodrendü elhajlási maximum az elsőrendütől? (4 pont)

Jedlik Ányos verseny, Győr

Megoldás. a) n=1130 osztás/cm,

b) 20,2 cm.

P. 3550. Egy, a Föld körül keringő ürhajóban egy 50 g tömegü, lebegő állapotban levő lézerceruza hirtelen bekapcsolódik, és egy órán keresztül 3 mW teljesítménnyel 500 nm hullámhosszúságú fényt sugároz.

a) Hány fotont sugároz ki a lézer ennyi idő alatt?

b) Becsüljük meg, hogy mekkora sebességre tesz szert és mekkora utat tesz meg az ürhajóban ennyi idő alatt a lézerceruza! (5 pont)

Wigner Jenő verseny, Békéscsaba

Megoldás. a) 2,7^.10¹⁹  foton.

b) v=7,2^.10^-7 m/s a lézerceruza végsebessége, és s=1,3 mm az elmozdulása.