A 2002. novemberi informatika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

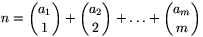I. 34. A binomiális együtthatók felhasználhatók számok speciális számrendszerben, az ún. binomiális számrendszerben való felírására. Rögzített m (2 $\le$ m $\le$ 50) esetén minden nemnegatív n (0 $\displaystyle \le$n $\displaystyle \le$10 000) szám egyértelműen felírható az alábbi formában: $n={a_1\choose1}+{a_2\choose2}+\dots+ {a_m\choose m}$ , ahol 0 $\displaystyle \le$a₁ < a₂ < ...< a_m.

Készítsünk programot (I34.pas, ...), amely beolvassa n és m értékét, majd kiírja a hozzá tartozó a₁,a₂,..., a_m értékét!

Pl.: n=41 esetén a₁ = 1, a₂ = 2, a₃ = 4, a₄ = 7, azaz

$\displaystyle 41={1\choose1}+{2\choose2}+{4\choose3}+{7\choose4}=1+1+4+35.$ (10 pont)

Megoldás:

Algoritmus
  Be: A felbontandó szám: N;
  Be: A tényezők száma: M;
  binom(100);

Ez az eljárás számolja ki a Pascal-háromszöget az N. soráig.

  n0:=n;

Az m darab tényezőt a legnagyobbtól kezdve határozzuk meg, úgy hogy közben az N értéke egyre csökken. A minden sorban a legnagyobb megfelelő elemet választjuk ki.

  ciklus i:=m-től 1-ig -1-esével
    j:=0;
    ciklus amíg b[j+1,i]<=n
      j:=j+1;
    ciklus vége;
    Ha n=0
      akkor
        a[i]:=0
      különben
        a[i]:=b[j,i];
        c[i]:=j;
    elágazás vége;
    n:=n-a[i];
  ciklus vége;

Végül kiíratjuk az összeget.

  Ki: n0 =;
  ciklus i:=1-től m-1-ig
    Ki: a[i] +; 
  ciklus vége;
  Ki: a[m];
  ciklus i:=1-től m-ig
    Ki: c[i];
  ciklus vége;
algoritmus vége;

A binom eljárás számolja ki a Pascal-háromszöget.

Eljárás binom(n: egész);
  változók
    i,j: egész;

Az első oszlopban és az átlóban egyesek vannak.

  ciklus i:=0-től n-ig
    b[i,i]:=1;
    b[i,0]:=1;
  ciklus vége;

A minden egyes elem a fölötte levő kettő összegével egyenlő.

  ciklus i:=1-től n-ig
    ciklus j:=1-től i-1-ig
      b[i,j]:=b[i-1,j-1]+b[i-1,j];
    ciklus vége;
  ciklus vége;
eljárás vége;

A megoldás Pascal nyelven: Letöltés

I. 35. Egy R sugarú, H magasságú henger palástja alján elhelyezünk egy hangyát. A hangya percenként M centimétert mászik felfelé. A hengert tengelye (ami a koordinátarendszer Z tengelye) körül megforgatjuk az óramutató járásával ellentétes irányban, egy fordulatot T perc alatt tesz meg. A hangya az (R,0,0) pontból indul, és pályáját az Y=0 síkra vetítjük. A vetítősugarak az Y-tengellyel ALFA fok szöget zárnak be (1. ábra).


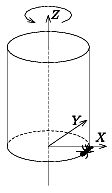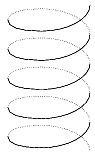1. ábra	2. ábra

Készítsünk programot (I35.pas, ...), amely beolvassa R (1 $\displaystyle \le$R$\displaystyle \le$50), H (1 $\displaystyle \le$ $\le$ H $\le$ 200), M (1 $\le$ M $\le$ H), T (1 $\le$ T $\le$ $\le$ 100) és ALFA (0 $\le$ ALFA<90) értékét, majd az Y=0 síkra vetített ábrát rajzol a hangya pályájáról a henger látható oldalán folytonos, hátoldalán pedig pontozott vonallal.

R=50, H=200, M=1, T=40, ALFA=30 esetén a 2. ábrán látható rajzot kapjuk. (10 pont)

Megoldás:

Hangya;
  változók
    x,y,z,tt: valós;
    m,h,r,t,alfa,y1,z1: valós;

Az adatok beolvasásakor az alfa dőlésszöget fokban olvassuk be, de rögtön radiánba átírjuk, mert azzal fogunk számolni.

  Be: A henger magassága: H;
  Be: A henger sugara: R;
  Be: Percenkénti felfelé haladás: M;
  Be: Egy forgás ideje: t;
  Be: Dőlésszőg: alfa; alfa:=-alfa/180*3.14159;
  x:=r; y:=0; z:=0; tt:=0; z1:=0;

Beállítjuk a grafikus felületet. A grafikus kurzort a kép közepére állítjuk.
Megjegyzés: Az XZ síkot fogjuk kirajzolni.

  Grafikus_Felület_Inicializálása;
  HelyezésXYhoz(Kerekít(x)+MaxX div 2,-Kerekít(z)+MaxY div 2);

Az aljától a tetejéig megyünk. tt az aktuális idő, lépésenként. Kiszámítjuk a koordinátákat, majd a pont helyétől függően kirajzoltatjuk az utat, mint egy szakasz.

  ciklus amíg z1<h+m/t
    tt:=tt+1;
    x:=r*cos(tt/t*2*3.14159);
    y1:=r*sin(tt/t*2*3.14159)*cos(alfa);
    z1:=m*tt;
    Ha y1>0
      akkor Vonal_Beállítása(Szaggatott)
      különben Vonal_Beállítása(Folytonos);
    elágazás vége;
    y:=y1*cos(alfa)+z1*sin(alfa);
    z:=-y1*sin(alfa)+z1*cos(alfa);
    SzakaszRajzolásXYig(Kerekít(x)+MaxX div 2,-Kerekít(z)+MaxY div 2);
  ciklus vége;

Végül lezárjuk a grafikus felületet.

  Grafikus_Felület_Lezárása;
algoritmus vége;

A megoldás Pascal nyelven: Letöltés

I. 36. A trinomiális tétel szerint:

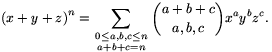
${(x+y+z)}^n=\sum_{\textstyle{0\le a,b,c\le n\atop a+b+c=n}}{a+b+c\choose a,b,c}x^ay^bz^c.$

A képletben használt zárójeles formula az ún. trinomiális együtthatókat tartalmazza, melyeket az alábbi képlettel is számolhatunk:

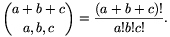
${a+b+c\choose a,b,c}=\frac{(a+b+c)!}{a!b!c!}.$

Az ebben a képletben szereplő faktoriális értékek azonban túlságosan nagyok, így kiszámításuk nem mindig végezhető el. A trinomiális együtthatók kiszámítása azonban visszavezethető binomiális együtthatók szorzatára is, ami ezt a problémát megoldja.

Készítsünk táblázatot (I36.xls), amelynek egy adott mezőjébe beírva n (n= a+b+c, n $\le$ 20) értékét, az alábbi jellegű táblázatot kapjuk a trinomiális együtthatókról!

Példa: n=5 esetén a táblázat:

a/b	0	1	2	3	4	5
0	1	5	10	10	5	1
1	5	20	30	20	5	0
2	10	30	30	10	0	0
3	10	20	10	0	0	0
4	5	5	0	0	0	0
5	1	0	0	0	0	0

(10 pont)

Megoldás:

Valóban a trinomiális együtthatók kiszámítása lehetséges a binomiális együtthatók szorzásával a következő módon:

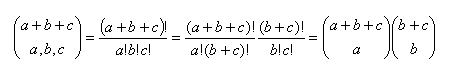
Így az első lépés a binomiális együtthatók kiszámítása oly módon, hogy az A oszlopba egyeseket (1) írunk míg az 1. sorba nullákat (0) a második mezőtől kezdve. A többi mezőben pedig kiszámítjuk a felette és az a melletti mező összegét. Így:

c6:=B5+C5

A B23-as cellában az N értékét írjuk.
A B25:L35-ös mezőben pedig kiíratjuk a trinomiális együtthatókat. A sorokban az "a" értéke, míg az oszlopokban a "b" értéke már egyértelműen meghatározza a "c"-t is, hiszen c=N-a-b. A cellákba nullát (0) vagy a megfelelő szorzatot kell írni, "a" és "b" függvényében (az indexek függvényében). Nullától indexelünk, és N-ig megyünk. Ezért vonunk le az oszlop és sor indexekből 2-t illetve 25-t. A binomiális együtthatók szorzatát is indexek segítségével számoljuk ki.
Az INDEX függvényhez meg kell adni a tartományt, ami a binomiális együtthatók értékeinek tartománya, vagyis az A1:U21 tartomány. Majd meg kell adni a sor illetve oszlop indexek értékét. Nullától indexelünk ezért mindenhol hozzá kell adni egyet. Kell az N-edik sorban a (b+c)-dik vagyis az (N-a)-dik oszlopban levő mező és az (N-a)-dik sorban az (N-a-b) vagyis a "c"-dik mező értéke a szorzáshoz.

c26:=HA(OSZLOP()-2+SOR()-25>$B$23;
        0;
        INDEX($A$1:$U$21;
              $B$23+1;
              $B$23-(OSZLOP()-2)+1
             )*
		INDEX($A$1:$U$21;
		      $B$23-(OSZLOP()-2)+1;
			  $B$23-(OSZLOP()-2)-(SOR()-25)+1
             )
       )

A megoldás Excelben: Letöltés

Már regisztráltál?
Új vendég vagy?