A 2002. novemberi számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3561. Az egyik balesetvédelmi reklám szerint ha 50 km/h sebességgel egy falnak ütközünk, annak ugyanaz a következménye, mintha a 4. emeletről estünk volna le. Vajon mekkora átlagos emeletmagasságra gondoltak? (3 pont)

Közli: Kopcsa József, Debrecen

(Mikola-verseny feladat)

Megoldás. 2,4 m.

P. 3562. Egy kertészetben gyümölcsös ládák szállítására földre fektetett acéllapot használnak, amelyet traktorral húznak. A lap tömege 20 kg, a lapon 400 kg gyümölcs van. A lap és a talaj közötti súrlódási együttható 0,6. Mennyire melegszik fel a lap 100 méteres úton, ha a súrlódási munka 40%-a az acéllap belső energiáját növeli? (3 pont)

,,Keresd a megoldást!'' verseny, Szeged

Megoldás. 11 C^o.

P. 3563. Két autó halad egyenes, keskeny úton egymás után. Mindkét jármű sebessége 72 km/h. Az elöl haladó autó fékezni kezd és egyenletesen lassulva megáll, miközben sebessége másodpercenként 5 m/s-mal csökken. A másik autó vezetőjének reakcióideje 1 másodperc, és sebességét másodpercenként 4 m/s-mal tudja csökkenteni.

a) Legalább mekkora legyen a követési távolság, hogy a járművek ne ütközzenek össze?

b) A minimális követési távolság betartása mellett az elöl haladó jármű fékezésének megkezdése után mennyi idő múlva lesznek a járművek 22 m távolságra egymástól? (4 pont)

Közli: Szegedi Ervin, Debrecen

(Mikola-verseny feladat)

Megoldás. a) 30 m;

b) 2 s, éppen akkor, amikor az elöl haladó autó megáll.

P. 3564. Hány darab 25 cm átmérőjű léggömböt lehet megtölteni a 0,1 m³ térfogatú, 1,5^.10⁷ Pa nyomású héliumgázzal töltött gázpalackból? A léggömbökben a nyomás 1,02^.10⁵ Pa-ra emelkedik, amikor a betöltött gáz hőmérséklete kiegyenlítődik a környezetével. A palackot napokkal előbb a töltőhelyre szállították. (4 pont)

Közli: Hilbert Margit, Szeged

(Tornyai-verseny feladat)

Megoldás. 1798 darabot, vagyis a megadott számadatok pontosságát is figyelembe véve kb. 1800 léggömböt lehet megtölteni.

P. 3565. Legalább mekkora térfogatú legyen az az edény, amelyben 15 liter 80 ^oC hőmérsékletű vizet úgy akarunk 25 ^oC-ra lehűteni, hogy 0 ^oC hőmérsékletű jeget teszünk bele, és nem akarjuk, hogy kifolyjon az edényből a víz? (3 pont)

Közli: Holics László, Budapest

Megoldás. Kb. 8 kg jégre van szükség, az edény tehát legalább 23 literes kell legyen.

P. 3566. Egy 1,5 méter magas faltól 2 méterre, a talaj szintjéről indítva át akarunk dobni a fal felett egy 5 kg tömegű súlygolyót.

a) Milyen irányú legyen a 8 m/s nagyságú kezdősebesség, hogy a súlygolyó a fal mögött a lehető legmesszebb essen le? Mekkora ez a távolság?

b) Mekkora legkisebb energiabefektetéssel hajítható át az adott helyről a súlygolyó? Milyen irányú ebben az esetben a kezdősebesség? (5 pont)

Közli: Szűcs József, Pécs

(Párkányi-verseny feladat)

Megoldás. a) 47,54^o és 6,4 m;

b) 98 J és 63,4^o.

Megjegyzés. Ezek a pályák nem szimmetrikusak a falra, a golyó nem vízszintesen repül át a fal felett. Ha minél messzebbre szeretnénk dobni (adott kezdősebességgel) a súlyt egy akadályon át, akkor a felszálló ágban kell áthaladjon az akadály felett. Ha viszont a legkisebb kezdősebességgel (energiával) akarjuk átjuttatni az akadályon, akkor a leszálló ágban kell átrepüljön a súlygolyó a fal felett.

P. 3567. Határozzuk meg az ábrán látható két besatírozott terület nagyságát integrálszámítás alkalmazása nélkül, valamilyen egyszerű fizikai gondolatmenettel!

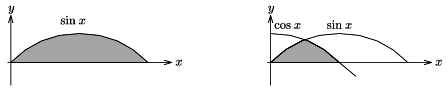
(5 pont)

Közli: Sári Péter, Budapest

Megoldás. Egy lehetséges megoldás: ha egy fonálingát megfelelő nagyságú érintő irányú erővel lassan kimozdítunk az alsó helyzetéből, az erő arányos a szögkitérés szinuszával, a végzett munka pedig (ami ennek az erőnek az integrálja) a nyert helyzeti energiával adható meg. Innen adódik, hogy a bal oldali terület 2, a jobb oldali pedig \(\displaystyle 2-\sqrt{2}\approx0{,}586\).

P. 3568. Vízszintes fém mennyezetre m tömegű pontszerű nehezékkel ellátott fonálingát kötünk. Az inga lengésideje kis kitérések esetén T₁. Ezután a nehezékre elektromos töltést viszünk, majd ismét kis kitérésű lengésbe hozzuk. A fonál szigetelő. Lengésidejét most T₂-nek mérjük.

Mekkora töltést vittünk a nehezékre?

(Adatok: m= 5 g, T₁=2,02 s, T₂=2,03 s, g=9,81 m/s².) (5 pont)

Közli: Légrádi Imre, Sopron

Megoldás. Amikor a nehezékre elektromos töltést adunk, az a fém mennyezeten elektromos megosztást hoz létre, és egy felfele ható, az inga kis kitérései mellett a pillanatnyi helyzettől függetlennek tekinthető erő lép fel, aminek a hatása olyan, mintha a g csökkenne. Ezt az erőt a tükörtöltés módszerével vehetjük figyelembe. Ennek alapján

\(\displaystyle Q={T_1^2\over T_2}{g\over2\pi^2}\sqrt{{mg\over k}\left(T_2^2-T_1^2\right)}=4{,}7\cdot10^{-7}\,{\rm C}.\)

P. 3569. Hidrogéngázzal töltött kisülési csövön működés közben 1,12 A áram folyik. Hány elektron halad át a cső keresztmetszetén másodpercenként, ha a negatív elektródából kilépő elektronok száma másodpercenként 3^.10¹⁸? (4 pont)

Közli: Radnai Gyula, Budapest

Megoldás. A kisülési csőben a hidrogén egy része ionizálódik, ennek során ugyanannyi pozitív töltés keletkezik, mint amennyi elektron válik szabaddá. Így amikor az áram 1,12 A, a 3^.10¹⁸ primer elektronnal együtt össesen 5^.10¹⁸ elektron halad át az egyik irányban, miközben 2^.10¹⁸ pozitív töltés megy a másik irányban.

P. 3570. U feszültségű szinuszos generátorra sorosan R ellenállást, L induktivitást és C kapacitást kapcsoltunk. Az induktivitás változtatható, növelése közben először az áram is nő, majd csökkenni kezd. Az áramerősség legnagyobb értéke I₀, ekkor a tekercs feszültsége U₀.

Az induktivitást tovább növelve a tekercs feszültsége tovább nő, elér egy maximális U_max  értéket, majd csökkenni kezd.

Határozzuk meg az U_max /U₀ arányt, és számítsuk ki értékét \(\displaystyle R=2\sqrt{2}X_C\) esetén! (5 pont)

Közli: Veres Zoltán, Margitta (Románia)

Megoldás. A körben folyó áram

\(\displaystyle I={U\over\sqrt{R^2+\left(X_L-X_C\right)^2}}\,, \)

és az induktvitáson eső feszültség

\(\displaystyle U_L={X_LU\over\sqrt{R^2+\left(X_L-X_C\right)^2}}\,. \)

Az áram akkor a legnagyobb, ha X_L=X_C, míg az U_L akkor, ha

X_L=(R²+X_C²)/X_C,

így

\(\displaystyle {U_{\rm max}\over U_0}={\sqrt{R^2+X_C^2}\over X_C}\,. \)

A kérdéses esetben ez az arányszám éppen 3.