A 2002. decemberi számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3571. Belül üres fémkocka külső élhosszúsága 5 mm, falvastagsága 1 mm. A fém sűrűsége 8400 kg/m³. Mi történik a kockával, ha a víz felszíne alatt tartjuk, majd elengedjük? (3 pont)

Komárom-Esztergom megyei ,,Ifjú Fizikus'' verseny nyomán

Megoldás. A belül üres kocka átlagsűrűsége 6586 kg/m³, tehát elsülyed.

P. 3572. Bizonyos mennyiségű ideális gáz az ábrán látható körfolyamatot végzi. Mennyi a gáz által végzett munka egy ciklus során?

(3 pont)

Közli: Veres Zoltán, Margitta

Megoldás. W=4p₁V₁.

P. 3573. Mekkora munka árán tudunk becsapni egy tömör fából készült, 24 kg tömegű ajtót úgy, hogy a széle 5 m/s sebességgel csapódjon az ajtótoknak? (4 pont)

Közli: Holics László, Budapest

Megoldás. Az ajtó szélességét a-val, tömegét M-mel jelölve a kérdéses munka legalább

$\displaystyle W=\frac{1}{2}\Theta\omega^2=\frac{1}{2}\, \frac{Ma^2}{3}\,\left(\frac{v}{a}\right)^2=\frac{Mv^2}{6}=100~\rm J.$

A légellenállás miatt ennél több munkát kell végeznünk.

P. 3574. Mennyi hő elvonásával készíthető 2 kg -5 ^oC hőmérsékletű túlhűtött vízből ugyanilyen hőmérsékletű jég? (4 pont)

Közli: Pálfalvi László, Pécs

Megoldás. A teljes energiaelvonás nem függ attól, milyen folyamaton keresztül fagyasztjuk ki a túlhűtött vizet. Ezért számolhatunk úgy, hogy a túlhűtött vizet először óvatosan felmelegítjük 0 ^oC-ra, azután a 0 ^oC-os vizet megfagyasztjuk, majd a jeget lehűtjük. Eszerint az elvonandó hő

Q=-mc_v$\displaystyle \Delta$T+mL₀+mc_j$\displaystyle \Delta$T=650 kJ.

P. 3575. M tömegű szánkón m tömegű kutya áll, amely u relatív sebességgel tud leugrani a szánkóról, majd v sebességgel tud utána szaladni és felugrani rá.

Elhanyagolva a szánkó súrlódását a hóborította vízszintes talajon, határozzuk meg, hogy végül is mekkora sebességre gyorsulhat fel így a szánkó és a kutya! Hányszor ugrik fel közben a kutya a szánkóra?

Legyen M=30 kg, m=10 kg, u=0,5 m/s, v=4 m/s. (5 pont)

Közli: Varga István, Békéscsaba

Megoldás. Ha a kutya egy w sebességű szánkóról u relatív sebességgel leugrik (azaz az ugrás után a kutyának a szánkótól mért sebessége u), az ugrás után a szánkó sebessége

$\displaystyle w^{\prime}=w+u{m\over m+M}. $

Ha most a kutya v sebességgel futva utoléri a szánkót és azzal felugrik rá, az új közös sebesség

$\displaystyle w^{\prime\prime}=w^{\prime}{M\over m+M}+v{m\over m+M}. $

Eszerint az n-edik es n+1-edik le-fel ugrás utáni sebességek közötti összefüggés

$\displaystyle w_{n+1}=\left(w_n+u{m\over m+M}\right){M\over m+M}+v{m\over m+M}\,. $

Innen, figyelembe véve, hogy w₀=0,

$\displaystyle w_n=w_1\sum_{k=1}^{n-1}\left({M\over m+M}\right)^k$, $\displaystyle w_1={m\over m+M}\left(u{M\over m+M}+v\right)$

Ha az n-edik leugrás után a sebesség már meghaladná v-t, már nem szabad a szánról leugrani, tehát

\(\displaystyle w_{n-1}+{m\over m+M}u< v

Ebből n=8 adódik, a végsebesség pedig w₈=3,94 m/s.

P. 3576. Rögzített, $\alpha$ =30^o-os hajlásszögű lejtőre egy m tömegű tömör hengert helyezünk. A hengert a palástjára csavart fonál segítségével a lejtőre merőlegesen F=x^.mg nagyságú erővel húzzuk. A henger csúszásmentesen gördül a lejtőn.

a) Határozzuk meg és ábrázoljuk a tapadási súrlódási erőt x függvényében!

b) Mekkorának kell választani x értékét, ha a lejtő felülete nagyon sima?

c) Legalább mekkorának kell lennie a tapadási súrlódási együtthatónak, ha a henger középpontja 2g gyorsulással mozog? (5 pont)

Közli: Kotek László, Pécs

Megoldás. Az alapegyenletek:

mgsin $\displaystyle \alpha$+S=ma,

$\displaystyle (mgx-S)R=\Theta\frac{a}{R}=\frac12maR,$

$\displaystyle \vert S\vert\leq mg(\cos\alpha+x)\mu.$

(Itt S a lejtővel párhuzamosan lefelé mutató súrlódási erő.) Ezekből

a) A súrlódási erő x függvényében:

$\displaystyle S=\frac{mg}{6}\,(4x-1).$

A csúszásmentes gördülés feltétele:

$\displaystyle \mu\geq{1\over3}\frac{\vert2x-\sin\alpha\vert} {\cos\alpha+x}={1\over3}\,\frac{\vert4x-1\vert} {\sqrt{3}+2x}.$

b) $\displaystyle \mu$=0 esetén is csúszásmentesen gördülhet a henger, ha

$\displaystyle x=\frac{\sin\alpha}2=\frac14.$

c) Ha a=2g,

$\displaystyle S=\frac32\,g$, $\displaystyle x=\frac52$ és $\displaystyle \mu\geq\frac{3}{\sqrt{3}+5}$.

P. 3577. Határozzuk meg egy téglalap keresztmetszetű toroid induktivitását! A tekercs menetszáma N, középkörének sugara R, a téglalap oldalai a és b. (Az a hosszúságú oldal párhuzamos a toroid tengelyével.)

Adatok: N=1000, R=10 cm, a=6 cm, b=4 cm. (5 pont)

Közli: Simon Péter, Pécs

Megoldás. Az adott toroid tekercset jó közelítéssel tekinthetjük egy $\displaystyle \ell$=2$\displaystyle \pi$R hosszú, A=a^.b keresztmetszetű, N menetes tekercsnek. Ekkor (légmagos tekercs esetén)

$\displaystyle L\approx{\mu_0N^2ab\over2\pi R}=4{,}80~\rm mH.$

Pontosabb eredményt kapunk, ha figyelembe vesszük, hogy a toroid belsejében a mágneses indukcióvektor nagysága a toroid tengelyétől mért r távolság függvényében változik:

$\displaystyle B(r)={\mu_0IN\over2\pi r}.$

Ezt is figyelembe véve

$\displaystyle L={\mu_0N^2a\over2\pi}\,\ln{2R+b\over2R-b}=4{,}86~\rm mH$

adódik. Látható, hogy a közelítő formulával számolt önindukciós együttható csak 1 százaléknyit tér el a pontosabb értéktől.

P. 3578. Egy felhő 0,1 mm átmérőjű vízcseppjei 10 V-ra töltődnek fel. A kicsiny cseppek 2,7 mm átmérőjű nagy cseppekké egyesülnek.

Mekkora lesz ezeknek a feszültsége? (4 pont)

Nagy László (1931-1987) feladata nyomán

Megoldás. Egy töltött gömb potenciálja U=kQ/r. A vízcseppek egyesülésekor a töltés 27³-szörösére, a sugár 27-szeresére nő, tehát a potenciál az eredeti érték 27²-szerese, azaz 7,3 kV lesz.

P. 3579. Ugyanakkora gyorsítófeszültség hatására hányszor nagyobb sebességre gyorsul fel vákuumban egy proton, mint egy $\displaystyle \alpha$-részecske, ha kezdeti sebességük elhanyagolható? (4 pont)

Közli: Radnai Gyula, Budapest

Megoldás. Ha a mozgás nemrelativisztikus (a sebességek elhanyagolhatók a fénysebesség mellett), akkor

$\displaystyle \frac{v_{\rm proton}}{v_{\rm alfa}}=\sqrt{2}.$

Ha viszont a gyorsítófeszültség sokkal nagyobb, mint 10⁹ V (ennél a gyorsítófeszültségnél éri el a proton mozgási energiája a nyugalmi energia nagyságrendjét), akkor a sebességarány egyre csökken és határesetben

$\displaystyle \frac{v_{\rm proton}}{v_{\rm alfa}}\rightarrow1.$

P. 3580. Egy űrállomás R=10 m sugarú forgó henger alakú tornatermében a földi g-nek megfelelő nagyságú ,,mesterséges gravitációt'' hoznak létre. Amikor nem használják a tornatermet, (rosszul értelmezett takarékosságból) egyenletes lassítással g-t a szokásos érték felére csökkentik.

Mennyi időre van szükség a lassításhoz, ha azt akarják, hogy a padlón lévő szőnyegek ne csússzanak el eredeti helyükről? (A tapadási súrlódási együttható a szőnyegek és a padló között legalább 0,1.) (4 pont)

Mennyire csökkenthető le a fékezés ideje, ha nem ragaszkodunk az egyenletes lassításhoz? Mennyi időre lenne szükség a teljes súlytalanság eléréséhez? (+2 pont)

Közli: Szokoly Gyula, Németország

Megoldás. A lassítás előtt $\displaystyle \omega$₀²R=g, a lassítás alatt

$\displaystyle \omega$=$\displaystyle \omega$₀-$\displaystyle \beta$t.

(Itt $\displaystyle \beta$>0 a lassulás mértéke.) A végállapotban $\displaystyle \omega=\omega_0/\sqrt{2}$, és annak a feltétele, hogy nincs megcsúszás

$\displaystyle \beta$R$\displaystyle \le$ $\mu$ $\omega$ ²R .

Eszerint $\beta$ = $\mu$ $\omega$ _min²= $\mu$ $\omega$ ₀²/2, a lassítás ideje pedig

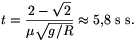
$t={2-\sqrt{2}\over\mu\sqrt{g/R}}\approx5{,}8~\rm s~\rm s.$

Ha végig úgy fékezzük a forgást, hogy éppen ne csússzanak meg a szőnyegek, akkor

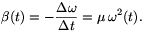
$\beta(t)=-\frac{\Delta\omega}{\Delta t}= \mu\,\omega^2(t).$

Ennek az egyenletnek (differenciálegyenletnek) a megoldása ,,elemi'' módszerrel is megkapható. Osszuk fel a fékezes megkezdésétől eltelt t időt $\Delta$ t_i intervallumokra (ezek legyenek olyan rövidek, hogy alattuk a fékezést egyenletesnek tekinthessük), és jelölje a szögsebesség értékét az i-edik intervallum végén $\omega$ _i. (A szögsebesség értéke az első intervallum elején $\omega$ ₀, az utolsó végén $\omega$ (t)). Még éppen nem csúszik meg a szőnyeg, ha

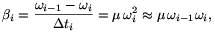
$\beta_i={\omega_{i-1}-\omega_{i}\over\Delta t_i}=\mu\,\omega_{i}^2\approx\mu\,\omega_{i-1}\omega_{i},$

azaz

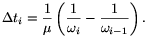
$\Delta t_i={1\over\mu}\left({1\over\omega_{i}}-{1\over\omega_{i-1}}\right).$

Mindkét oldalt felösszegezve az összes intervallumra (mivel a jobb oldalon a közbülső tagok kiesnek)

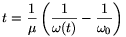
$t={1\over\mu}\left({1\over\omega(t)}- {1\over\omega_{0}}\right)$

adódik, ahonnan

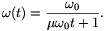
$\omega(t)={\omega_0\over\mu\omega_0 t+1}.$

Innen a fékezés ideje

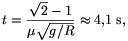
$t={\sqrt{2}-1\over\mu\sqrt{g/R}}\approx4{,}1~\rm s,$

ez egy 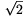$\sqrt{2}$ faktorral rövidebb idő, mint az egyenletes fékezésé.

A fenti képletből az is látható, hogy véges idő alatt $\omega$ (t) nem csökkenthető nullára, tehát a teljes súlytalanság állapota ilyen módon nem érhető el, csak tetszés szerint megközelíthető.

Már regisztráltál?
Új vendég vagy?