A 2003. februári számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3591. Egy metróállomás 3,5 m széles kijáratán percenként átlagosan 70 ember halad át azonos irányban. A ,,népsűrűség'' 0,4 fő/m².

Mekkora az emberek átlagos sebessége?

(3 pont)

Közli: Varga Zsuzsa, Szeged
Tarján Imre emlékverseny, Szolnok

Megoldás. Az átlagsebesség

$\displaystyle v={70~{{\rm ember}\over{\rm perc}}\over{3{,}5~{\rm m}\cdot0{,}4~{{\rm ember}\over{\rm m}^2}}}=3{,}0~{{\rm km}\over{\rm h}}=0{,}83~{{\rm m}\over{\rm s}}.$

P. 3592. Galvánelemből, akkumulátorból és egy ohmos ellenállásból összeállított elágazás nélküli áramkörben az akkumulátoron és az ellenálláson is 9 V feszültség mérhető.

Mekkora feszültség mérhető az ugyancsak 9 V-os, de nem zérus belső ellenállású galvánelemen, és mit állapíthatunk meg az ellenállás nagyságáról?

(4 pont)

Közli: Radnai Gyula, Budapest

Megoldás. Ha a galvánelemet és az akkumulátort azonos polaritással kötöttük sorba, akkor a galvánelemen mérhető feszültség nulla, ellenkező polaritású kapcsolásnál pedig 18 V.

Az előbbi esetben a galvánelem belső ellenállásán éppen az elem elektromotoros erejének megfelelő feszültség esik, a terhelő ellenállás nagysága pedig úgy aránylik a galvánelem belső ellenállásához, mint ahogy az akkumulátor feszültsége aránylik a galvánelem üresjárati feszültségéhez. Ellentétes polaritású kapcsolásnál a galvánelem elektromotoros ereje legalább 18 V kell legyen.

P. 3593.

Egy vízszintes síkú, R sugarú mágneskorong $\displaystyle \omega$₀ szögsebességgel forog a középpontján átmenő, rögzített függőleges tengely körül. Kis magasságból ráesik egy ugyanilyen, kezdetben nyugvó korong, és azonnal hozzátapad. (A két korong középpontja R-nél kisebb távolságra lesz egymástól.)

Mekkora közös szögsebességgel fog forogni a két korong?

(4 pont)

Közli: Simon Péter, Pécs

Megoldás. Ha a két mágneskorong középpontjának távolsága kR lesz (k<1), akkor a közös szögsebességük

$\displaystyle \omega={\omega_0\over2\left(1+k^2\right)}.$

P. 3594.

Fonálingát derékszögben kitérítünk, majd lökés nélkül elengedjük. Az ábra szerinti AP vagy PB szakaszt teszi meg az inga rövidebb idő alatt?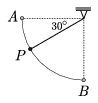

(5 pont)

Közli: Károlyházy Frigyes, Budapest
Mikola Sándor fizikaverseny, Gyöngyös

Megoldás. Az időtartamok ,,pontos'' számértékének kiszámítása felsőbb matematikai eszközöket igényel, de erre most nincs szükség; enélkül is belátható, hogy t_AP>t_PB. A mozgás első szakasza ugyanis legalább annyi ideig tart, mint a szabadesés ideje az A és P pontok szintkülönbségének megfelelő h=$\displaystyle \ell$sin 30^o távolságon ($\displaystyle \ell$ a fonal hossza):

$\displaystyle t_{AP$\sqrt{2h\over a}>\sqrt{\ell\over g}.">

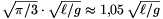Megjegyzés: Még élesebb egyenlőtlenséget kaphatunk abból a tényből, hogy az inga érintőleges gyorsulása a kezdőpillanatot leszámítva mindvégig g-nél kisebb, emiatt az $\displaystyle \ell$ $\pi$ /6 út megtételéhez legalább $\sqrt{\pi/3}\cdot\sqrt{\ell/g}\approx1{,}05\,\sqrt{\ell/g}$ időre van szüksége.

Másrészt - az energiamegmaradás tételéből - tudjuk, hogy a P pontban az inga sebessége

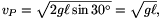
$v_P=\sqrt{2g\ell\sin30^\circ}=\sqrt{g\ell},$

a PB ív C felelőpontjában pedig a sebesség

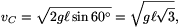
$v_C=\sqrt{2g\ell\sin60^\circ}=\sqrt{g\ell\sqrt{3}},$

továbbá azt, hogy a sebesség a megtett út (és az eltelt idő) monoton növekvő függvénye. Emiatt

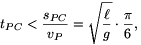
$t_{PC}<{s_{PC}\over v_P}=\sqrt{\ell\over g}\cdot{\pi\over6},$

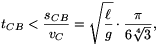
$t_{CB}<{s_{CB}\over v_C}=\sqrt{\ell\over g}\cdot{\pi\over6\root4\of{3}},$

és így

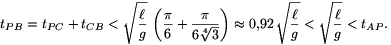
$t_{PB}=t_{PC}+t_{CB}<\sqrt{\ell\over g}\, \left({\pi\over6}+{\pi\over6\root4\of{3}}\right)\approx0{,}92\,\sqrt{\ell\over g}<\sqrt{\ell\over g}<t_{AP}.$

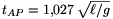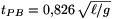Megjegyzés: Még pontosabb közelítésekkel (a mozgás nagyon sok kis részre osztásával) kiszámítható, hogy (4 jegyre pontosan) $t_{AP}=1{,}027\,\sqrt{\ell/g}$ és $t_{PB}=0{,}826\,\sqrt{\ell/g}$ .

P. 3595. Félgömb alakú mélyedést hozunk létre egy hasáb belsejében. Az M tömegű hasáb a vízszintes asztalon szabadon elmozdulhat. A nyugvó hasáb P pontjánál elengedünk egy m tömegű pontszerű testet. Mekkora erővel nyomja a hasáb a kis testet a $\varphi$ szögű helyzetben? (A súrlódás mindenütt elhanyagolható.)

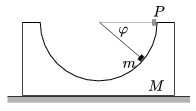
(5 pont)

Közli: Pálfalvi László, Pécs

Megoldás.

$N=mg\sin\varphi\cdot\left[{M\over M+m\cos^2\varphi}+{2(m+M)M\over(M+m\cos^2\varphi)^2}\right].$

P. 3596. Egy 3 literes tartályban 2,2^.10⁶ Pa nyomású és 80 ^oC hőmérsékletű, egy 5 literesben pedig 1,3^.10⁵ Pa nyomású és 5 ^oC-os oxigéngáz van. A két tartályt egy rövid csővel összekötjük. Mekkora lesz bennük a közös nyomás akkor, amikor a gáz felveszi a szoba 23 ^oC-os hőmérsékletét? Mennyi gáz áramlott át eközben a csövön?

(4 pont)

Közli: Hilbert Margit, Szeged
Tornyai Sándor fizikaverseny, Hódmezővásárhely

Megoldás. A mólszámok:

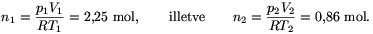
$n_1={p_1V_1\over RT_1}=2{,}25~{\rm mol},\qquad{\rm illetve}\qquad n_2={p_2V_2\over RT_2}=0{,}86~{\rm mol}.$

A kialakuló nyomás:

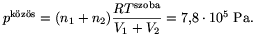
$p^{\rm k\ddot oz\ddot os} =(n_1+n_2){RT^{\rm szoba}\over V_1+V_2}=7{,}8\cdot10^5~\rm Pa.$

A végállapotban

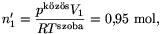
$n_1^\prime={p^{\rm k\ddot oz\ddot os}V_1\over RT^{\rm szoba}}=0{,}95~\rm mol,$

a csövön tehát 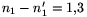$n_1-n_1^\prime=1{,}3$ mólnyi gáz áramlott át a 3 literes tartályból az 5 literesbe. Ez kb. 42 g oxigénnek felel meg.

P. 3597. Bizonyos mennyiségű nemesgáz állapotváltozása során Q hőt vesz fel, miközben térfogata V₁-ről V₂-re nő, nyomása térfogatával arányosan növekszik. Mekkora V₃ térfogatra tágulna ki a gáz a kezdeti V₁ térfogatról, ha úgy venne fel Q hőt, hogy nyomása mindvégig a kezdeti értéken maradna?

(Adatok: V₁=5 dm³, V₂=8 dm³.)

(4 pont)

Közli: Légrádi Imre, Sopron

Megoldás.

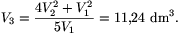
$V_3={4V_2^2+V_1^2\over5V_1}=11{,}24~\rm dm^3.$

P. 3598. Vákuumban elhelyezett síkkondenzátor A területű fémlemezei vízszintes szigetelő szálon súrlódásmentesen csúszhatnak. A bal oldali lemez tömege m, töltése Q, a jobb oldali lemez tömege 2m, töltése -2Q. A lemezek kezdetben rögzítettek, távolságuk 3d.

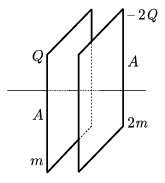
a) Mekkora a lemezek közötti elektromos mező energiája?

b) Egy adott pillanatban a lemezek rögzítését megszüntetjük. Mekkora lesz a lemezek sebessége akkor, amikor távolságuk már csak d?

(5 pont)

Közli: Kotek László, Pécs
Párkányi László fizikaverseny, Pécs

Megoldás. Mindkét kondenzátorlemez polarizálódik. A bal oldali lemez külső felületére -Q/2, a belsőre 3Q/2 töltés kerül. A jobb oldali lemez belső oldalán -3Q/2, a külsőn -Q/2 töltés fog elhelyezkedni. (Ebben az állapotban a legkisebb a rendszer elektrosztikus energiája.)

a) Az elektrosztatikus térenergia a lemezek között

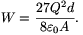
$W={27Q^2d\over8\varepsilon_0A}.$

b) A lemezek között ható vonzóerő F=Q²/( $\varepsilon$ ₀A), a testek gyorsulása

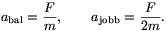
$a_{\rm bal}={F\over m},\qquad a_{\rm jobb}={F\over2m}.$

A kérdéses pillanatban a lemezek elmozdulása

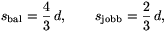
$s_{\rm bal}={4\over3}\,d,\qquad s_{\rm jobb}={2\over3}\,d,$

a sebességek pedig

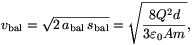
$v_{\rm bal}=\sqrt{2\,a_{\rm bal}\,s_{\rm bal}}=\sqrt{8Q^2d\over3\varepsilon_0Am},$

illetve

$v_{\rm jobb}=\sqrt{2\,a_{\rm jobb}\,s_{\rm jobb}}=\sqrt{2Q^2d\over3\varepsilon_0Am}.$

A két lemez sebessége ellentétes irányú, és mivel v_jobb=v_bal/2, az összimpulzusuk nulla.

P. 3599. Debrecenben 1984-ben méréssel megállapították, hogy a maghasadás egyik lehetséges termékeként keletkező ⁸⁵Kr izotóp $\beta$ ^- bomlásának aktivitás-koncentrációja 0,8 Bq/m³. Becsüljük meg, hány kg kripton bomlik el óránként a légkörben?

(5 pont)

Közli: Kopcsa József, Debrecen

Megoldás. Tekintsük a légkör azon kriptonatomjait, melyek éppen 1 óra alatt bomlanak el. Ezek darabszám-sűrűsége a Föld felszínén

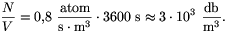
${N\over V}=0{,}8~{{\rm atom}\over{\rm s}\cdot{\rm m^3}}\cdot3600~{\rm s}\approx3\cdot10^3~{{\rm db}\over{\rm m^3}}.$

Innen a pV=NkT gáztörvény felhasználásával (k a Boltzmann-állandó, és T $\approx$ 300 K) a kérdéses mennyiségű kriptongáz parciális nyomása tengerszinten:

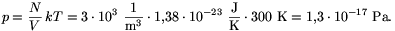
$p={N\over V}\,kT=3\cdot10^3~{1\over{\rm m^3}}\cdot1{,}38\cdot10^{-23} ~{{\rm J}\over{\rm K}}\cdot300~{\rm K}=1{,}3\cdot10^{-17}~{\rm Pa}.$

Ennek a nyomásnak és a Föld mintegy 5^.10¹⁴ m² nagyságú felszínének szorzata 6^.10^-3 N erőt ad, ami a kérdéses kripton mg súlyával egyenlő. Innen a keresett tömeg:

m $\approx$ 6^.10^-4 kg.

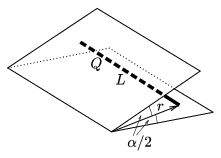
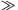P. 3600. Két nagyméretű, földelt fémlap $\alpha$ szöget zár be egymással. A szögfelező síkban, a síkok metszésvonalától r távolságban egy L hosszúságú (L $\gg$ r), egyenletesen elosztott Q töltésű, vékony pálca található. Mekkora erő hat a pálcára az elektromos megosztás következtében, ha

a) $\alpha$ =180^o,

b) $\alpha$ =18^o.

(5 pont)

Közli: Gnädig Péter, Budapest

Megoldás. Egy hosszú, egyenletesen töltött pálca elektromos terének nagysága a pálcától x távolságban (a Gauss-törvény szerint)

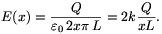
$E(x)={Q\over\varepsilon_0\,2x\pi\,L}=2k{Q\over xL}.$

Ha n= $\pi$ / $\alpha$ egész szám, akkor - a tükörtöltések módszerével - belátható, hogy a pálcára ható erő nagysága n-től független:

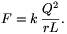
$F=k\,{Q^2\over rL}.$

Megjegyzés: Felsőbb matematikai eszközökkel igazolható, hogy ez az eredmény akkor is érvényes marad, ha n nem egész.

Már regisztráltál?
Új vendég vagy?