A 2003 márciusi A-jelű matematika feladatok megoldása

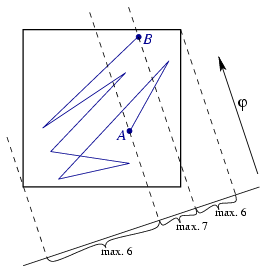
A. 314. Adott egy egységnyi oldalú négyzetben egy töröttvonal úgy, hogy bármely egyenes, amely egy csúcsára sem illeszkedik, legfeljebb hét oldalát metszi. Legfeljebb milyen hosszú lehet a töröttvonal?

Soukup Lajos ötletéből

Megoldásvázlat. Legyen a töröttvonal hossza l, végpontjai A és B. Tetszőleges $\displaystyle \varphi$ irányban legyen a négyzet vetületének hossza n($\displaystyle \varphi$), az AB szakasz vetületének hossza h($\displaystyle \varphi$), a töröttvonalat alkotó szakaszok vetületének összege v($\displaystyle \varphi$).

Ha egy $\displaystyle \varphi$ irányú egyenes nem választja el egymástól az A és B pontokat, akkor a töröttvonalat páros sokszor, tehát legfeljebb csak 6-szor metszi. Ezért

v($\displaystyle \varphi$)$\displaystyle \le$6n($\displaystyle \varphi$)+h($\displaystyle \varphi$).

(Lásd az 1. ábrát.)

1. ábra	2. ábra

Vegyük az egyenlőtlenség $\displaystyle \varphi$ szerinti átlagát, azaz integráljunk $\displaystyle \varphi$ szerint 0-tól $\displaystyle \pi$-ig, és osszuk el az integrált $\displaystyle \pi$-vel. Könnyen ellenőrizhető, hogy egy x hosszú szakasz vetületének átlaga $\displaystyle {2\over\pi}x$, az egységnégyzeté $\displaystyle {4\over\pi}$, tehát

$\displaystyle {2\over\pi}l\le6\cdot{4\over\pi}+{2\over\pi}AB,$

$\displaystyle l\le12+AB\le12+\sqrt2.$

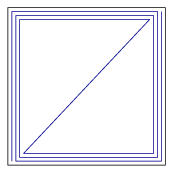
Ez az eredmény éles. Ha a töröttvonal háromszor végigfut a négyzet kerületén és tartalmazza az egyik átlót, akkor megfelel a feltételnek és a hossza éppen $\displaystyle 12+\sqrt2$ (2. ábra).

A. 315. Egy szabályos (n²+n+1)-szögnek kiválasztottuk n+1 csúcsát. Bizonyítsuk be, hogy ha az n szám 12k-2 alakú, akkor a kiválasztott csúcsok közötti távolságok nem lehetnek mind különbözők.

Megoldás. Tegyük fel indirekten, hogy n=12k-2 és a kiválasztott csúcsok között futó $\displaystyle {n+1\choose2}$ átló mind különböző hosszúságú. A szabályos (n²+n+1)-szögben éppen ennyiféle hosszúságú átló van.

Az n²+n+1 szám osztható 3-mal. Számozzuk meg a csúcsokat sorban 1-től (n²+n+1)-ig, és csoportosítsuk a kiválasztott csúcsok indexeit modulo 3. A három csoportba eső indexek száma legyen a, b, illetve c; a kiválasztott csúcsok száma összesen a+b+c=n+1=12k-1.

Számoljuk össze azokat az átlókat, amelyek hossza a kerületen mérve hárommal osztható, tehát a harmad-, hatod-, kilenced- stb. szomszédos átlókat. Ezek száma $\displaystyle \big[{n+1\choose2}/3\big]=24k^2-6k$. Ilyen átlókat úgy kaphatunk, hogy azonos csoportba tartozó csúcsokat kötünk össze, tehát

$\displaystyle 24k^2-6k={a\choose2}+{b\choose2}+{c\choose2}.$

Ebből

a²+b²+c²=48k-12k+a+b+c=48k-1.

A 8k-1 és speciálisan a 48k-1 alakú számok nem írhatók fel három négyzetszám összegeként. Az indirekt feltevésből ellentmondásra jutottunk.

A. 316. Adott n pozitív egész számhoz tekintsük azon A$\displaystyle \subset${1,2,...,n} halmazokat, amelyekben az x+y$\displaystyle \equiv$u+v (mod n) kongruenciának nincs más megoldása, mint az x=u, y=v, illetve x=v, y=u triviális megoldások. Legyen f(n) az ilyen halmazok elemszámának maximuma.

a) Bizonyítsuk be, hogy $\displaystyle f(n)<\sqrt{n}+1$.

b) Mutassunk példát végtelen sok olyan n-re, amikor $\displaystyle f(n$\sqrt{n}-1">.

A 2002. évi Schweitzer-verseny 4. feladata nyomán

Megoldásvázlat. a) Tekintsük az A-beli elemek különbségeit modulo n; az x-y és y-x különbségeket különböztessük meg. Ha |A|=k, akkor összesen k(k-1) ilyen van, egyik sem 0. Ha valamelyik két különbség megegyezne, akkor azokból nemtriviális megoldást kapnánk. Ezért k(k-1)$\displaystyle \le$n-1, amiből $\displaystyle k\le{1\over2}+\sqrt{n-{3\over4}}<\sqrt{n}+1$.

b) Legyen p tetszőleges prímszám és n=p(p-1); legyen továbbá g egy primitív gyök modulo p. Az A halmaz álljon azokból az x számokból, amelyekre x$\displaystyle \equiv$g^x (mod p). Először is bebizonyítjuk, hogy a modulo n maradékosztályok között pontosan p-1 ilyen van.

Legyen r egy tetszőleges, 0-tól különböző maradék modulo p, és keressük az x$\displaystyle \equiv$r, g^x$\displaystyle \equiv$r (mod p) kongruenciarendszer megoldásait. Az x számot az x$\displaystyle \equiv$r kongruencia meghatározza modulo p, a g^x$\displaystyle \equiv$r kongruencia pedig meghatározza modulo (p-1). Mivel p és p-1 relatív prímek, a kínai maradéktétel szerint a megoldások az egyik modulo p(p-1) maradékosztály elemei.

Konkrét példa: Legyen p=7, n=42 és g=3. (A 3 primitív gyök modulo 7, mivel a 3 hatványai 7-tel osztva minden 0-tól különböző maradékot kiadnak: 3⁰=1, 3¹=3, 3²$\displaystyle \equiv$2, 3³$\displaystyle \equiv$6, 3⁴$\displaystyle \equiv$4 és 3⁵$\displaystyle \equiv$5 (mod 7).) Az x$\displaystyle \equiv$3^x (mod 7) kongruencia megoldásait az alábbi táblázatban foglaltuk össze:

r 3x$\displaystyle \equiv$r (mod 7) megoldása x$\displaystyle \equiv$r, 3x$\displaystyle \equiv$r (mod 7) megoldása 1 x$\displaystyle \equiv$0 (mod 6) x$\displaystyle \equiv$36 (mod 42) 2 x$\displaystyle \equiv$2 (mod 6) x$\displaystyle \equiv$2 (mod 42) 3 x$\displaystyle \equiv$1 (mod 6) x$\displaystyle \equiv$31 (mod 42) 4 x$\displaystyle \equiv$4 (mod 6) x$\displaystyle \equiv$4 (mod 42) 5 x$\displaystyle \equiv$5 (mod 6) x$\displaystyle \equiv$5 (mod 42) 6 x$\displaystyle \equiv$3 (mod 6) x$\displaystyle \equiv$27 (mod 42)

Az A halmaz elemei tehát: 2,4,5,27,31,36.

Végül megmutatjuk, hogy az A halmaz eleget tesz a feltételeknek. Mint láttuk, az A halmaz elemei páronként különbözők modulo p. Tetszőleges x,y$\displaystyle \in$A esetén az x+y érték meghatározza a szorzatot is modulo p, hiszen xy$\displaystyle \equiv$g^xg^y$\displaystyle \equiv$g^x+y. Ha tehát ismerjük x+y-t, akkor meghatározhatjuk xy-t is modulo p, és felírhatunk egy modulo p másodfokú egyenletet, amelynek két gyöke x és y. A másodfokú egyenlet pedig - a sorrendtől eltekintve - egyértelműen meghatározza a gyökpárt. Ha tehát ismerjük x+y értékét, akkor x és y értékét is meghatározhatjuk modulo p; ez pedig meghatározza magát a két elemet is.

Az előbbi példában tegyük fel, hogy azokat az x,y elemeket keressük, amelyekre x+y$\displaystyle \equiv$16 (mod 42). Ekkor x+y$\displaystyle \equiv$2 (mod 7) és xy$\displaystyle \equiv$3¹⁶$\displaystyle \equiv$4 (mod 7). Az x és y számok tehát a t²-2t+4$\displaystyle \equiv$0 (mod 7) kongruencia gyökei. Mivel t²-2t+4$\displaystyle \equiv$(t-3)(t-6) (mod 7), az x,y számok egyike 7-tel osztva 3-at ad maradékul a másik pedig 6-ot. Az egyik szám tehát a 31, a másik a 27.

A bemutatott konstrukcióban n=p(p-1) és |A|=p-1, ezért $\displaystyle f(n)\ge p-$\sqrt{n}-1">. Végtelen sok olyan n-et sikerült tehát találni, amikor $\displaystyle f(n$\sqrt{n}-1">.