 |
A 2003. áprilisi számban kitűzött fizika elméleti feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
P. 3611. Tekintsük a pizzát r sugarú, m tömegű homogén, vékony korongnak! Egy 20o-os szeletet már kivágtunk, és megettük. A sugár hány százalékával tolódott el a pizza súlypontja?
(3 pont)
Közli: Varga Zsuzsa, Szeged
Tornyai Sándor fizikaverseny, Hódmezővásárhely
Megoldás. A sugár kb. 4 százalékával.
P. 3612. Egy kötél végére függesztett vödör ingamozgást végez. Csökken vagy nő a lengésidő, ha a vödörből a víz a vödör alján lévő lyukon keresztül lassanként kicsöpög?
(5 pont)
A Vermes Miklós fizikaverseny (Sopron) egyik feladata nyomán
Megoldás. Ha a kötél hossza sokkal nagyobb, mint a vödör mérete, és a víz mennyisége lassan csökken a vödörben, akkor a mozgás közelítőleg egy matematikai inga lengéseivel írható le. Ennek lengésidejét a rendszer tömegközéppontjának helyzete határozza meg.
Ha a vödörben sok víz van, akkor a tömegközéppont lassan süllyed, a lengésidő tehát növekszik. Amikor viszont a vödörben már csak kevés víz van, a tömegközéppont helyzetét egyre inkább a vödör határozza meg. A vízszint csökkenésével a tömegközéppont ekkor már emelkedik, a lengésidő tehát csökken.
Nem túl hosszú kötél esetén a rendszer mozgását egy olyan fizikai ingaként tárgyalhatjuk, melynek tömege, tehetetlenségi nyomatéka, valamint tömegközéppontjának helyzete egyszerre változik, s ezen változások együttese határozza meg a lengésidő módosulását.
P. 3613. Vashuzalból zárt karikát készítettünk, és az ábra szerint egy negyedkörének végpontjaiban egy-egy vezetéket forrasztottunk hozzá.
Mekkora a karikához vezető huzalokban folyó áram erőssége, ha a negyedkörnyi huzaldarab ellenállása 0,2 \(\displaystyle \Omega\), és a forrasztási pontok között 0,6 V feszültség mérhető?
(3 pont)
Közli: Holics László, Budapest
Megoldás. 4 A.
P. 3614. Adjunk becslést arra, milyen vastag rétegben lehetne egyenletesen lefedni a szárazföldet annyi búzaszemmel, amennyit a sakkjáték állítólagos feltalálója kért jutalmul a királytól. (Az első mezőre 1 szemet kért, és minden következőre kétszer annyit, mint az előzőre.)
(4 pont)
Kőnig Dénes (1884-1944) nyomán
Megoldás. A búzaszemek száma 264-1\(\displaystyle \approx\)2.1019. A szárazföldek összterülete kb. 1,5.1014 m2. A búzaszemeket 3 mm átmérőjű, 1 cm hosszú hengereknek, vagy néhány milliméter átmérőjű gömböknek tekintve a ,,búzatakaró'' vastagságára kb. 5-10 mm adódik. A pontos számértéknek nincs jelentősége, csupán a becslés nagyságrendjét szabad komolyan venni.
P. 3615. Vízszintes felületen, egymástól 4 m távolságra lévő, azonos tömegű két test egyszerre indul el egymás irányába, majd a pálya közepén rugalmatlanul ütköznek. A jobb oldali, állandó sebességgel mozgó test kezdősebessége kétszerese a bal oldali, 0,5 m/s2 gyorsulással mozgó test kezdősebességének.
a) Mekkorák a kezdősebességek?
b) A mechanikai energia hány százaléka veszett el a rugalmatlan ütközés során?
(4 pont)
Közli: Kotek László, Pécs
Megoldás. a) 1 m/s. b) 96,15 %.
P. 3616. Dugattyúval elzárt hengerben lévő levegő nyomása a térfogatával arányosan nő. A folyamat során a levegő 90 kJ hőt vesz fel.
Mennyi munkát végez a táguló gáz, és mennyivel nő az energiája?
(4 pont)
Közli: Légrádi Imre, Sopron
Megoldás. W=15 kJ. \(\displaystyle \Delta\)E=75 kJ.
P. 3617. 100 V feszültségre feltöltött kondenzátort egy ellenálláson keresztül kisütünk. A kisütő áram erőssége a kezdeti 100 \(\displaystyle \mu\)A értékről 2 másodpercenként 60%-kal csökken.
a) Mekkora a kisütő ellenállás?
b) Mekkora a kondenzátor kapacitása?
c) Mennyi idő elteltével csökken az áram erőssége 0,41 \(\displaystyle \mu\)A-re?
(5 pont)
Közli: Szegedi Ervin, Debrecen
Nagy László fizikaverseny, Kazincbarcika
Megoldás. a) 1 M\(\displaystyle \Omega\), b) 2,2 \(\displaystyle \mu\)F, c) 12 s.
P. 3618. Két végtelen, egyenként d vastagságú, +\(\displaystyle \varrho\), illetve -\(\displaystyle \varrho\) térfogati töltéssűrűségű lemez közvetlenül egymás mellett helyezkedik el.
Adjuk meg és ábrázoljuk az elektromos térerősséget, valamint a potenciált a lemezektől mért távolság függvényében!
(5 pont)
Közli: Kotek Gyula, Pécs
Megoldás. A térerősség a lemezeken kívül nulla, középen a legnagyobb, nevezetesen E(0)=\(\displaystyle \varrho\)d/\(\displaystyle \varepsilon\)0, és az egyes lemezeken belül lineárisan (a távolsággal arányosan) változik. Az E(x) függvény grafikonja ,,háztető alakú''.
A potenciálfüggvény E(x) görbe alatti területe (valamely önkényesen választott ponttól kiindulva). Ez két - egymáshoz folytonosan és törésmentesen illeszkedő - parabola, melyek egyenlete
\(\displaystyle U(x)=-{\varrho\over2\varepsilon_0}(x^2+2dx+d^2),\qquad{\rm ha}\quad-d\le x\le0,\)
illetve
\(\displaystyle U(x)={\varrho\over2\varepsilon_0}(x^2-2dx-d^2),\qquad{\rm ha}\quad0\le x\le d.\)
A lemezeken kívül a potenciál állandó, x\(\displaystyle \le\)0 esetén nulla, az x\(\displaystyle \ge\)d tartományban pedig U0=-\(\displaystyle \varrho\)d2/\(\displaystyle \varepsilon\)0.
P. 3619. Egy elektronnyaláb merőlegesen lép be olyan homogén mágneses térbe, ahol a Lorentz-erő R sugarú körív befutására készteti. A mágneses tér ,,szélessége'' \(\displaystyle \ell\)=R/5, és tőle L=5R távolságban van az a fluoreszkáló ernyő, ahová az elektronok becsapódnak. Mekkora az elektronnyaláb eltérülése az ernyőn? Mi történne, ha a gyorsítófeszültséget a) negyed, b) huszonötöd részére csökkentenénk?
(4 pont)
Közli: Veres Zoltán, Margitta (Románia)
Megoldás. Az eltérülés 5,2 \(\displaystyle \ell\).
Negyed gyorsítófeszültségnél a pályasugár az eredeti érték fele, az eltérülés pedig 11,1 \(\displaystyle \ell\) lesz. Huszonötöd részére lecsökkentett gyorsítófeszültségnél a pályasugár az eredeti érték ötöde, tehát \(\displaystyle \ell\). Ilyenkor az elektronnyaláb nem lép ki a mágneses mező jobb oldali határán, hanem egy félkört tesz meg, majd az eredeti mozgásirányával éppen ellentétesen mozog tovább (visszapattan a mágneses mezőről).
P. 3620. Két, egyenként 10 N/m rugóállandójú gumiszál kapcsolódik a vízszintes, súrlódásmentes talajon lévő 1 kg tömegű test két oldalához. A gumiszálakat bizonyos \(\displaystyle \Delta\)
hosszúsággal megnyújtva, végeiket rögzítjük. Ezután a testet 2
-lel kitérítjük az egyik rögzítési pont felé, majd elengedjük.
Határozzuk meg a kialakuló rezgőmozgás periódusidejét!
(5 pont)
Közli: Pálfalvi László, Pécs
Megoldás. 1,57 s.
P. 3621. Egy dugattyúval elzárt hengeres edényben gáz van. A henger fala szigetelő, alaplapja és a dugattyú azonban fémből készült, és síkkondenzátorként viselkedik, ha elektromos feszültséget kapcsolunk rá. Kezdetben a fegyverzetek közötti távolság d0, a bezárt gáz nyomása megegyezik a külső légnyomással.
Hogyan változik a fegyverzetek közötti távolság, ha U feszültségre kapcsoljuk a ,,kondenzátort''? Tegyük fel, hogy a gáz hőmérséklete állandó.
(5 pont)
Közli: Varga István, Békéscsaba
Megoldás. A dugattyúnak nem túl nagy feszültség,
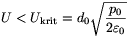
esetén két egyensúlyi helyzete is lehet, amikor a fegyverzetek távolsága
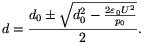
A nagyobb távolságnak megfelelő eset stabil, a kisebb instabil egyensúlyi helyzet. Amennyiben U=Ukrit, már csak egyetlen istabil egyesúlyi helyzet van, ha pedig U>Ukrit, a dugattyú addig mozog, míg a fegyverzetek össze nem érnek (vagy a gáz már nem írható le az ideális gáz állapotegyenleteivel).