A 2003. májusi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3642.

(4 pont)

Megoldás: Tekintsünk két ilyen számot. Mindkét szám jegyeinek összege 28=3^.9+1, vagyis minkét szám 9-cel osztva 1 maradékot ad. Ha a két szám hányadosa egész szám, akkor a hányados is 1 maradékot ad 9-cel osztva. Mivel a hányados nyilván 1 és 7 közé esik, ez csak úgy lehetséges, ha a hányados értéke 1, vagyis ha a két szám megegyezik. A számok között tehát nincs olyan, amely osztója lenne egy tőle különbözőnek.

B.3643.

(3 pont)

Megoldás: A kocka egy csúcsát az adott csúcsot nem tartalmazó lapokkal összekötve a kockát fel tudjuk osztani három egybevágó négyzet alapú gúlára. Ha egy ilyen gúla alaplapja az ABCD négyzet, csúcsa pedig az A' pont, ahol AA' merőleges a négyzet síkjára, akkor azt az A', A és C csúcsokra illeszkedő sík két egybevágó tetraéderre osztja. Mindhárom gúlát ilyen módon kettévágva tehát a keresett felosztáshoz jutunk.

B.3644.

(4 pont)

Megoldás: Legyen a háromszög oldala egységnyi hosszú és jelölje a három kör sugarát a,b,c, ahol a\(\displaystyle \ge\)b\(\displaystyle \ge\)c. A feltételek miatt \(\displaystyle a\le\sqrt{3}/2\). Nyilván feltehetjük, hogy a\(\displaystyle \ge\)1/2 és b=c=1-a. Ha ezen feltételek teljesülnek, akkor a három kör a kívánt módon helyezkedik el, a háromszögből pedig együttesen

\(\displaystyle {\pi\over6}(a^2+b^2+c^2)={\pi\over6}(3a^2-4a+2)\)

területű részt fednek le. Azt kell tehát megválaszolnunk, hogy az \(\displaystyle 1/2\le a\le\sqrt{3}/2\) feltétel mellett mikor lesz a 3a²-4a+2 kifejezés értéke a lehető legnagyobb. Mivel

\(\displaystyle 3a^2-4a+2=3\Bigl(a-{2\over3}\Bigr)^2+{2\over3}\)

és egyszerű számolással ellenőrizhető, hogy

\(\displaystyle {2\over3}-{1\over2}<{\sqrt{3}\over2}-{2\over3},\)

a kifejezés értéke \(\displaystyle a=\sqrt{3}/2\) esetén lesz a lehető legnagyobb.

A körök sugarát tehát úgy kell megválasztani, hogy az egyik kör sugara a háromszög oldalának \(\displaystyle \sqrt{3}/2\)-szöröse, a másik két kör sugara pedig a háromszög oldalának \(\displaystyle 1-\sqrt{3}/2\)-szöröse legyen.

B.3645.

\(\displaystyle f\left(\frac{x+y}{3}\right)=\frac{f(x)+f(y)}{2}. \)

(3 pont)

Megoldás: Tegyük fel, hogy f(1)=a, ekkor az f(1)=(f(1)+f(2))/2 feltétel alapján f(2)=a, f(2)=(f(3)+f(3))/2 miatt pedig f(3) értéke is a. Tegyük fel hogy valamilyen k pozitív egész számra már igazoltuk, hogy

f(1)=f(2)=...=f(3k)=a.

Ekkor k+2\(\displaystyle \le\)3k miatt f(k+1)=f(k+2)=a, és ezért

\(\displaystyle {f(3k+1)+f(2)\over2}={f(3k+2)+f(1)\over2}=a= {f(3k+3)+f(3)\over2}\)

alapján f(3k+1)=f(3k+2)=f(3k+3)=a is teljesül. A teljes indukció elve miatt tehát minden n pozitív egész számra f(n)=a. Ugyanakkor f(n)=(f(4n)+f(-n))/2 miatt f(-n)=a is igaz.

Az f függvény tehát minden 0-tól különböző egész számra ugyanazt az értéket veszi fel. Az pedig nyilvánvaló, hogy minden ilyen konstans függvény kielégíti az előírt feltételt.

B.3646.

(4 pont)

Kiss Sándor (Szatmárnémeti) javaslata nyomán

Megoldás:

Az a=BC oldalhoz hozzáírt kör érintse a BC oldalt a D pontban, a b=AC és c=AB oldalakak egyenesét pedig rendre az E és F pontokban. Ekkor AE=AF=s, CD=CE=s-b és BD=BF=s-c, ahol s=(a+b+c)/2 a háromszög kerületének fele. Az a oldalhoz hozzáírt DEF háromszög T_a területét úgy számolhatjuk ki, hogy az AEF háromszög területéből levonjuk a BDF, CDE és ABC háromszögek területét. Ez utóbbit T-vel jelölve, az AEF háromszög területe T(s/b)(s/c), hiszen a két háromszög egyik szöge közös, azt ezt közrefogó megfelelő oldalak aránya pedig AE/AC=s/b illetve AF/AB=s/c. Mivel az ABC és DBF szögek kiegészítő szögek, melyeknek szinusza egyenlő, kapjuk hogy a BDF háromszög területe az ABC háromszög területének (BD/BC)(BF/BA)=(s-c)²/(ac)-szerese, a CDE háromszög területe pedig ugyanilyen alapon T(s-b)²/(ab). Ezért

\(\displaystyle T_a=T\Bigl({s^2\over bc}-{(s-b)^2\over ab}-{(s-c)^2\over ac}-1\Bigr)= {2Ts(s-b)(s-c)\over abc}.\)

Szimmetria okok miatt a b oldalhoz hozzáírt háromszög területe

\(\displaystyle T_b={2Ts(s-a)(s-c)\over abc},\)

a két terület aránya pedig T_a/T_b=(s-b)/(s-a).

B.3647.

(4 pont)

Megoldás:

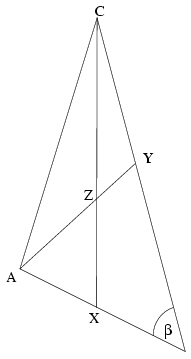
A BAY és ZCY háromszögekre a szinusz tételt felírva a megfelelő oldalak egyenlősége alapján kapjuk, hogy az ABY és AYB szögek szinuszainak aránya megegyezik a CZY és CYZ szögek szinuszainak arányával. Mivel az AYB és CYZ szögek kiegészítő szögek, az ABY és CZY szögek szinusza is egyenlő. Ha az első szög \(\displaystyle \beta\) a második pedig \(\displaystyle \pi\)-\(\displaystyle \beta\), akkor az AYB szög \(\displaystyle \pi\)-\(\displaystyle \beta\)-nál kisebb, amiért is a CYZ szög \(\displaystyle \beta\)-nál nagyobb, vagyis a ZCY háromszög szögeinek összege \(\displaystyle \pi\)-nél nagyobb, ami nem lehetséges. Ezért a CZY szög is \(\displaystyle \beta\), tehát az XBY és XZY szögek kiegészítő szögek, vagyis az XBYZ négyszög húrnégyszög. A B,X,Y,Z pontok tehát valóban egy körön vannak.

B.3648.

2y+x-x²-y² = 0

z-x+y-y(x+z) = 0

-2y+z-y²-z² = 0.

(4 pont)

Megoldás: Az a=x-1/2, c=z-1/2 helyettesítéssel az egyenletrendszer

\(\displaystyle 2y-y^2-a^2=-{1\over4},\ c-a-y(a+c)=0,\ -2y-y^2-c^2=-{1\over4}\)

alakot ölti. Az első egyenletből a harmadikat kivonva c²-a²=-4y adódik, ha tehát a második egyenletet a+c-vel megszorozzuk, akkor a 4y+y(a+c)²=0 összefüggést nyerjük. Innen (a+c)²\(\displaystyle \ne\)-4 miatt y=0, vagyis a²=c²=1/4, amit a második egyenletből adódó c=a feltétellel is összevetve kapjuk, hogy a=c=1/2 vagy a=c=-1/2.

Az egyenletrendszernek tehát két megoldása lehetséges, ezek x=z=1, y=0, illetve x=y=z=0. Mindkét számhármas meg is felel a feltételeknek.

B.3649.

(4 pont)

Megoldás: Teljes indukcióval azonnal belátható, hogy minden m, n természetes számra a_n+m=2^ma_n+(2^m-1). Mivel a sorozat képzési szabálya miatt a_n páratlan pozitív egész, az Euler-Fermat tétel alapján létezik olyan m pozitív egész, nevezetesen az a_n-nél nem nagyobb, a_n-hez relatív prím pozitív egészek száma, amelyre a_n | 2^m-1. Ekkor azonban a k=n+m jelöléssel élve nyilván a_n osztója lesz a nála nagyobb a_k számnak.

B.3650.

cos 3\(\displaystyle \alpha\)+ cos 3\(\displaystyle \beta\)+ cos 3\(\displaystyle \gamma\)=1.

Bizonyítsuk be, hogy a háromszögnek van 120^o-os szöge.

(5 pont)

Megoldás: Az x=3\(\displaystyle \alpha\), y=3\(\displaystyle \beta\) jelöléssel élve 0<x,y,x+y<3\(\displaystyle \pi\) és

cos 3\(\displaystyle \gamma\)=cos (3\(\displaystyle \pi\)-x-y)=-cos (x+y)=sin xsin y-cos xcos y.

Ezért átrendezés után összefüggésünk a

sin xsin y=(1-cos x)(1-cos y)

alakot ölti. Mindkét oldalt négyzetre emelve a trigonometrikus Pithagorasz tétel alapján az

(1-cos² x)(1-cos² y)=(1-cos x)²(1-cos y)²

összefüggést kapjuk, ahonnan vagy 1-cos x=0, mely esetben x=2\(\displaystyle \pi\), \(\displaystyle \alpha\)=120^o, vagy 1-cos y=0, azaz \(\displaystyle \beta\)=120^o, vagy pedig a pozitív (1-cos x)(1-cos y) szorzattal leosztva

(1+cos x)(1+cos y)=(1-cos x)(1-cos y).

Ez utóbbi esetben átrendezés után cos x+cos y=0 adódik, tehát x\(\displaystyle \pm\)y=(2k+1)\(\displaystyle \pi\) valamilyen k egész számra. x-y=(2k+1)\(\displaystyle \pi\) nem lehetséges, mert ekkor sin x=-sin y lenne, amiből

0\(\displaystyle \ge\)sin xsin y=(1-cos x)(1-cos y)>0

következne, ami nyilván lehetetlen. Ezért ebben az esetben x+y=(2k+1)\(\displaystyle \pi\), amit a 0<x+y<3\(\displaystyle \pi\) feltétellel összeveteve x+y=\(\displaystyle \pi\), \(\displaystyle \alpha\)+\(\displaystyle \beta\)=\(\displaystyle \pi\)/3 adódik, vagyis most \(\displaystyle \gamma\)=120^o.

B.3651.

Hány 2-nél nagyobb osztatlan szám van?

(5 pont)

Megoldás: Legyen p₁=2, p₂=3, p₃=5, és általában p_k a k-adik pozitív prímszám. Ha az n osztatlan szám nagyobb, mint p_k², akkor szükségképpen osztható p_k-val, ennélfogva P_k=p₁p₂...p_k-val is. Másrészt ha n\(\displaystyle \le\)p_k+1² és n osztható P_k-val, akkor n nyilván osztatlan. Ennek alapján a 4-nél nagyobb, ugyanakkor 49-nél nem nagyobb osztatlan számok a következők: 6,8,12,18,24,30. Ezenkívül a 3 és a 4 is osztatlan számok. Megmutatjuk, hogy 49-nél nagyobb osztatlan szám nem létezik, vagyis összesen nyolc 2-nél nagyobb osztatlan szám van.

Tegyük fel, hogy az n osztatlan szám nagyobb, mint 49=p₄². Ekkor a fentiek alapján n osztható P₄=210-zel, következésképpen p₆²=169<210\(\displaystyle \le\)n. Ezért n osztható P₆-tal is, tehát n\(\displaystyle \ge\)P₆. Mivel P₆>p₈², az is igaz, hogy n\(\displaystyle \ge\)P₈. Ebből már világosan látszik, hogy elegendő igazolni az alábbi állítást: minden k\(\displaystyle \ge\)4 egész szám esetén p_2k+2²<P_2k, ugyanis ebből a teljes indukció elve alapján következik, hogy minden k\(\displaystyle \ge\)2 egész számra n\(\displaystyle \ge\)P_2k>k, ami viszont nem lehetséges.

Legyen Q=P_k+1, és tekintsük a következő k+1 számot:

\(\displaystyle Q-1,\ a_i={Q\over p_i}-p_i\ (2\le i\le k+1).\)

Ezen számok mindegyike páratlan, és nem osztható a p₂,p₃,...,p_k+1 számok egyikével sem. Ezek a számok egymáshoz is relatív prímek, ugyanis ha egy q prímszám osztója Q-1-nek és a_i-nek is, akkor osztója a Q-1-p_ia_i=p_i²-1=(p_i-1)(p_i+1) számnak is, tehát q |  p_i-1 vagy q |  p_i+1. Mivel p_i-1 és p_i+1 páros számok, ezen számok minden prímosztója p_i-nél kisebb, de mint láttuk, a p_i-nél kisebb prímek nem osztói a_i-nek, ez tehát nem lehetséges. Ugyanígy, ha a q prím osztja a_i-t és a_j-t is (i<j), akkor osztója a p_ia_i-p_ja_j=p_j²-p_i²=(p_j-p_i)(p_j+p_i) számnak is, ám a p_j-p_i és p_j+p_i számok prímosztói p_j-nél kisebbek. A Q-1, a_i=Q/p_i-p_i számoknak van tehát k+1 különböző prímosztója, melyek mindegyike nagyobb, mint p_k+1. Ezen számok abszolút értékben mind Q-nál kisebbek, ezért p_2k+2<Q. Minthogy p₁p₂p₃p₄p₅<p₆p₇p₈\(\displaystyle \le\)p_2k-2p_2k-1p_2k,

p_2k+2²<Q²=(p₁p₂...p_k+1)(p₁p₂p₃p₄p₅)(p₆p₇...p_k+1)\(\displaystyle \le\)

\(\displaystyle \le\)(p₁p₂...p_k+1)(p_2k-2p_2k-1p_2k)(p_k+2p_k+3...p_2k-3)=P_2k,

ami az állítást igazolja.