A 2003. májusi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 720. Egy iskolában a tanév során három kirándulást szerveztek. Az első kiránduláson a résztvevő tanulók 75%-a, a másodikon 60%-a volt fiú. A harmadik kirándulásra pontosan azok a tanulók mentek el, akik legalább az egyik kiránduláson részt vettek. Mutassuk meg, hogy a harmadik kiránduláson sem volt kevesebb fiú, mint lány.

Megoldás. Az a ,,legrosszabb'' eset, ha csak olyan fiúk kirándultak, akik mindkét kiránduláson részt vettek, a kiránduló lányok közül pedig senki nem vett részt mindkét kiránduláson. (Könnyen belátható, hogy ezen a szituáción akárhol változtathatunk is, nő a fiúk aránya a harmadik kiránduláson.)

Ennek a legegyszerűbb megvalósítása:

Ekkor a 3. kiránduláson (3 fiú és 3 lány) éppen 50% a fiúk aránya.

C. 721. A 0-tól különböző a, b, c valós számokra kiszámítjuk az

$\displaystyle \frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{abc}{|abc|} $

értéket. Hány különböző eredményt kaphatunk?

Megoldás. Minden tört értéke +1 vagy -1, és ez csak a, b és c előjelétől függ, ezek sorrendjétől nem. Így összesen 4-féle előjelváltozat létezik, amikből már következik az $\displaystyle abc\over|abc|$ tört előjele is:

Tehát összesen 3-féle értéke lehet a vizsgált összegnek: 4, 0 és -4.

C. 722. Tetszőleges x valós számra legyen f(x) a 4x+1, x+2, -2x+4 értékek minimuma. Mennyi f(x) legnagyobb értéke?

Megoldás. Vázoljuk közös koordinátarendszerben a három lineáris függvényt: f₁(x)=4x+1, f₂(x)=x+2, f₃(x)=-2x+4.

Látható, hogy másként

f(x)=4x+1, ha x<1/3,

f(x)=x+2, ha 1/3$\displaystyle \le$x<2/3,

f(x)=-2x+4, ha 2/3$\displaystyle \le$x.

Így f szigorúan monoton nő, ha x<2/3 és szigorúan monoton csökken, ha x>2/3. Maximuma x=2/3-nál $\displaystyle f(2/3)=2{2\over3}.$

C. 723. Egy első generációs robotmanó csak egyenesen tud haladni. Irányváltoztatáshoz le kell állítani, majd a kívánt irányba fordítva újból elindítani. Egy 1 méter széles körfolyosón, amelynek belső kerülete 30 méter, legalább hányszor kell leállítani a robotot ahhoz, hogy a folyosót körbejárva visszaérjen kiindulási pontjába? (A robotmanó kiterjedése elhanyagolható.)

Megoldás. Nézzük, mekkora középponti szög tartozik a robotmanó leállítás nélküli lehetséges legnagyobb elmozdulásához.

Az ábra alapján:

$\displaystyle \cos{\alpha\over2}={r\over R}={r\over r+1}={{30/2\pi}\over{(30+2\pi)/2\pi}}={30\over30+2\pi}.$

Innen $\displaystyle {\alpha\over2}\approx34,226^{\circ}$, $\displaystyle \alpha$ $\approx$ 68,45^o.

Így öt szakasszal még nem tud körbejárni (5 $\alpha$ <360^o). Hattal viszont igen, például hat egyforma 60^o-os középponti szöghöz tartozó elmozdulással. De ehhez csak ötször kell leállítani és elfordítani.

C. 724. Egy egyenes hasáb alapja derékszögű háromszög. A háromszög egyik befogója akkora, mint a hasáb magassága. Másik befogójának és átfogójának hossza együtt 8 cm. Legfeljebb mekkora lehet a hasáb térfogata?

Megoldás.

a+c=8 cm

Pitagorasz tétele alapján a²+b²=64-16a+a², ebből b²=64-16a.

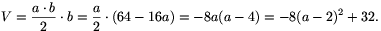
$V={a\cdot b\over2}\cdot b={a\over2}\cdot\left(64-16a\right)=-8a(a-4)=-8(a-2)^2+32.$

Tehát a térfogat a=2 cm esetén maximális: V_max=32cm³. (Ekkor c=6 cm, 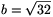$b=\sqrt{32}$ cm.)

Már regisztráltál?
Új vendég vagy?