A 2003. májusi számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3622. Lehet-e készíteni olyan kaleidoszkópot, amelybe belenézve hétágú csillagot láthatunk?

(3 pont)

Közli: R. Szendrei Julianna, Budapest

Megoldás. Igen, készíthetünk ilyen kaleidoszkópot: két síktükröt

\(\displaystyle {180^\circ\over7}\approx25{,}7^\circ\)

szögben kell egymáshoz illesztenünk.

P. 3623. Nagyméretű, föld alatti tartályból, 3 m mélységből másodpercenként 3 kg benzint (\(\displaystyle \varrho\)=860 kg/m³) szeretnénk felszivattyúzni. A szivattyú kifolyónyílása 10 cm² keresztmetszetű. Legalább mekkora legyen a szivattyú teljesítménye?

(4 pont)

Közli: Pálfalvi László, Pécs

Megoldás. A szivattyú egységnyi idő alatt végzett munkája legalább akkora, amekkora a felszívott benzin gravitációs helyzeti energiájának növekedése és a mozgási energiája együttesen. (Ténylegesen ennél több, hiszen súrlódási veszteségek is fellépnek.) Számszerűen: P>107 W.

P. 3624. Az ábrán látható, egyik végén beforrasztott, vékony cső függőleges síkban helyezkedik el. A cső vízszintes, 3L hosszú részében lévő L hosszúságú higanyoszlop L hosszúságú oxigéngázt zár el. A külső p₀ légnyomás L magasságú higanyoszlop nyomásával egyenlő. A környezet hőmérsékletét növelve a bezárt gáz térfogata megkétszereződik, miközben a gáz Q=7 J hőt vesz fel a környezetéből.

a) Mekkora munkát végzett a táguló gáz?

b) Mennyi hőt kellett volna közölni a gázzal, hogy térfogata ne kétszeresére, hanem háromszorosára nőjön?

(5 pont)

Közli: Kotek László, Pécs
(Mikola-verseny feladat)

Megoldás. a) A munkavégzés 5 J, ez a légkör ,,megemelésére'' fordítódik.

b) Q=30 J. Ebből 5 J a tágulási munka, 25 J pedig a belső energia növekedése.

P. 3625. Dugattyúval elzárt hengerben lévő gáz adiabatikus tágulása közben 9446 J munkát végez. Ezután az elért nyomáson addig melegítjük, amíg hőmérséklete az eredeti értékre áll vissza. Eközben a gáz 6140 J munkát végez. Mekkora a gázra jellemző \(\displaystyle \kappa\)=c_p/c_V hányados? Melyik gázról lehet szó?

(4 pont)

Közli: Légrádi Imre, Sopron

Megoldás. \(\displaystyle \kappa\)=1,65. A gáz - a táblázati adatok szerint - argon vagy neon lehet.

P. 3626. Egy levegővel telt, vékonyfalú szappanbuborékot lassan melegítünk. Mekkora lehet ebben a folyamatban a gáz mólhője? (A külső nyomás mindvégig állandó, a párolgástól és a telített gőz nyomásától tekintsünk el!)

(5 pont)

Közli: Vigh Máté, Pécs, PTE Babits M. Gyak. Gimn.

Megoldás. \(\displaystyle C=C_V+R{\displaystyle{p_0r+4\alpha}\over{\displaystyle p_0r+(8/3)\alpha}},\) ahol r a buborék sugara, \(\displaystyle \alpha\) a felületi feszültség, p₀ a külső légnyomás, R pedig a gázállandó. Mivel C_V=5R/2, a kérdéses mólhő 7R/2 és 4R közötti érték kell legyen. Reális adatok mellett p₀r\(\displaystyle \gg\), így C7R/2.

P. 3627. Andi és Bandi azon vitatkoznak, hogy ha egy nemesgázt lehűtünk olyan alacsony hőmérsékletre, hogy megszilárdul, milyen típusú kristályrács alakul ki benne. Abban egyetértenek, hogy a lehető legsűrűbb elrendeződés fog kialakulni.

Andi azt mondja, hogy az egymással párhuzamos síkokban négyzetrácsban helyezkednek el az atomok, és bármelyik rácssík atomjai az alattuk lévő rácssík atomjai közötti ,,hézagokban ülnek''.

Bandi azt mondja, hogy ő ezt a ,,hézagokban ülő'' elvet már a síkon belül is alkalmazná, s így nem négyzetrácsba, hanem szabályos háromszögrácsba rendezné el az atomokat.

Kinek van igaza? Melyik a sűrűbb elrendeződés? Mekkora a szabályos gömböknek tekinthető atomok ,,térkitöltése'' az A illetve a B esetben?

(5 pont)

Közli: Radnai Gyula, Budapest

Megoldás. Mindkét térkitöltés ugyanolyan sűrű, a gömbök térfogata a teljes térfogat 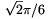része, vagyis kb. 74 százaléka.

P. 3628. Az erdőben a fák véletlenszerűen helyezkednek el úgy, hogy hektáronként átlagosan 600 fa van. Minden fa törzse 30 cm átmérőjű hengernek tekinthető. Egy kiránduláson a gyerekek azt játsszák, hogy egyikük szemét bekötik, aki azután szabadon bolyong a fák között. Mindig egyenes pályán halad, de amikor egy fába ütközik, véletlenszerűen megváltoztatja mozgásirányát. Becsüljük meg, hogy átlagosan mekkora távolságot tesz meg két ütközés között a gyerek, ha a probléma szempontjából ő is egy 30 cm átmérőjű hengernek tekinthető!

(4 pont)

Közli: Szegedi Ervin, Debrecen
(Nagy László verseny, Kazincbarcika)

Megoldás. Az ,,átlagos szabad úthossz'' 28 méternek becsülhető.

P. 3629. Hogyan változik a mozgási energia kétszeresének és a gravitációs energiának az összege, ha a műholdat 100 km-rel magasabb körpályára állítják át?

(4 pont)

Közli: Bakonyi Gábor, Budapest

Megoldás. A gravitációs helyzeti energia minden körpályán keringő műholdra a mozgási energia -2-szerese. Így a kérdéses mennyiség a pályasugártól függetlenül nulla, tehát a pályamódosítás során nem változik.

P. 3630. Hat pontszerű, Q nagyságú töltés helyezkedik el egy szabályos hatszög csúcsaiban. Mekkora pontszerű töltés van a hatszög közepén, ha a rendszer egyensúlyban van? Mennyi a rendszer elektrosztatikus kölcsönhatási energiája? Milyen típusú az egyensúly?

(5 pont)

Közli: Veres Zoltán, Margitta (Románia)

Megoldás. A középső töltés nagysága

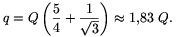
Az egyensúly labilis, és az összenergia E=0.

P. 3631. A csernobili katasztrófa után a helybeliek pajzsmirigyének ¹³¹I-tól származó aktivitása 1000 Bq körül volt. Mennyi idő alatt csökkent ez 100 Bq alá? A 131-es tömegszámú jódizotóp radioaktív, fizikai felezési ideje 8 nap, biológiai felezési ideje 120 nap.

(4 pont)

Közli: Kopcsa József, Debrecen

Megoldás. Kb. 25 nap alatt.