 |
A 2003. októberi C-jelű matematika gyakorlatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
C. 730. Hány megoldása van az \(\displaystyle \left[\frac{x}{10}\right]= \left[\frac{x}{11}\right]+1\) egyenletnek az egész számok körében?
Megoldás. Írjuk fel x-et 11k+r alakban, ahol 0\(\displaystyle \le\)r\(\displaystyle \le\)10. Ekkor az eredeti egyenlet
\(\displaystyle \left[{11k+r\over10}\right]=\left[{11k+r\over11}\right]+1 \)
alakban írható. Ebből
\(\displaystyle k+\left[{k+r\over10}\right]=k+\left[{r\over11}\right]+1, \)
vagyis
\(\displaystyle \left[{k+r\over10}\right]=1 \)
adódik.
Ebből \(\displaystyle 1\le{k+r\over10}<2\), 10\(\displaystyle \le\)k+r\(\displaystyle \le\)19. Tekintetbe véve, hogy 0\(\displaystyle \le\)r\(\displaystyle \le\)10, 110 ilyen számpár létezik.
C. 731. Az ABCD trapéz AB alapjára, mint átmérőre írt kör érinti a CD alapot és felezi az AD és BC szárakat. Mekkorák a trapéz szögei?
XII. Nemzetközi Magyar Matematika Verseny
Megoldás. A trapéz szimmetrikus. Jelölje az AB alap középpontját O, CD-ét P; messe a kör az AD szárat E-ben, az OD-t F-ben.
<<\epsfbox>>
E rajta van az AB és a CD egyeneseinek középpárhuzamosán (ez jelenti azt, hogy a kör a szárakat a felezőpontjukban metszi), így az EPO háromszög tengelyesen szimmetrikus, EO=EP. Mivel OE és OP is a kör sugara, így OE=OP, tehát az OEP háromszög egyenlő oldalú, szögei 60o -osak.
A BAD szög eszerint 75o -os.
C. 732. Igazoljuk, hogy tetszőleges a és b nemnegatív valós számokra fennáll az \(\displaystyle a+b+\frac{1}{2}\ge\sqrt{a}+\sqrt{b}\) egyenlőtlenség.
Megoldás. A feladatbeli kifejezés ekvivalens a \(\displaystyle \left(\sqrt a-{1\over2}\right)^2+\left(\sqrt b-{1\over2}\right)^2\ge0\) egyenlőtlenséggel, amely nyilvánvaló.
C. 733. Egy szabályos háromszög oldalait (azonos körüljárás szerint) felosztottuk p:q arányban. Az osztópontok összekötésével kapott háromszög területe az eredeti háromszög területének \(\displaystyle \frac{19}{64}\)-ed része. Mekkora a p:q arány?
Javasolta: Koncz Levente, Budapest
Megoldás. Feltehető, hogy a háromszög oldalainak hossza 1, és ezeket osztottuk q és p hosszúságú részekre, azaz p+q=1.
A kisebb háromszögön kívül megmaradó három háromszög együttes területe \(\displaystyle {p\cdot q\cdot\sin60^{\circ}\over2}\cdot3\), ez a teljes területnek, \(\displaystyle (p+q)^2\cdot{\sqrt3\over2}\cdot{1\over2}={\sqrt3\over2}\cdot{1\over2}\)-nek a \(\displaystyle {45\over64}\) része:
\(\displaystyle {p\cdot q\cdot\sin60^{\circ}\over2}\cdot3={45\over64}\cdot{\sqrt3\over2}\cdot{1\over2}. \)
Mivel \(\displaystyle \sin60^{\circ}={\sqrt3\over2}\), azért
\(\displaystyle {p\cdot q}\cdot3={45\over64}, \)
azaz \(\displaystyle pq={15\over64}\). A p+q=1 összefüggésből az egyik érték \(\displaystyle {3\over8}\), a másik \(\displaystyle {5\over8}\), a p:q arány tehát 3/5 vagy 5/3.
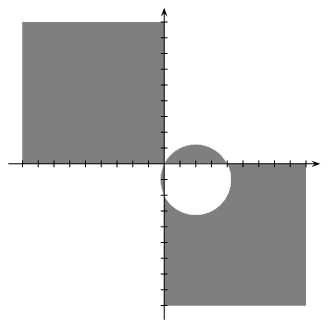
C. 734. Ábrázoljuk a koordinátarendszerben azokat a P(x;y) pontokat, amelyek koordinátáira \(\displaystyle \frac{2+y}{x}<\frac{4-x}{y}\).
Megoldás.
x,y\(\displaystyle \ne\)0
A feladatot két részre bontjuk x és y előjelétől függően:
1. x>0, y>0 vagy x<0, y<0
Az eredeti kifejezés az (x-2)2+(y+1)2<5 egyenlőtlenséggel ekvilvalens. A (2;-1) középpontú, \(\displaystyle \sqrt5\) sugarú körnek az I., illetve a III. síknegyedbe eső belső pontjai tartoznak a megoldáshalmazhoz.
2. x<0, y>0 vagy x>0, y<0
Az eredetivel ekvivalens (x-2)2+(y+1)2>5 kifejezés a (2;-1) középpontú \(\displaystyle \sqrt5\) sugarú kör külső pontjai, tehát a II. és a IV. síknegyedbe eső, ezen a körön kívül található pontok lesznek megfelelőek. A kör nem metsz bele a II. síknegyedbe (mert átmegy az origón), ott tehát minden pont megoldás.
