A 2003. novemberi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 735.Az egységnyi oldalú ABCD négyzet AB, BC, CD, DA oldalán fölvesszük az A₁, B₁, C₁, D₁ pontokat úgy, hogy $\displaystyle AA_1=BB_1=CC_1=DD_1=\frac{1}{5}$. Mekkora az A₁B₁C₁D₁ négyszög területe?

Megoldás. Az A₁B₁C₁D₁ négyszög területe az egységnégyzet területénél az abból ,,leeső'' négy egybevágó derékszögű háromszög területösszegével kisebb, azaz $\displaystyle 1-4\cdot\frac{1}{2}\cdot\frac{1}{5}\cdot\frac{4}{5}=\frac{17}{25}$. (Egyébként az A₁B₁C₁D₁ négyszög is négyzet, oldalának hossza Pitagorasz tétele szerint $\displaystyle \sqrt{(\frac{4}{5})^2+(\frac{1}{5})^2}= \frac{\sqrt{17}}{5}$, ezért a területe $\displaystyle (\frac{\sqrt{17}}{5})^2= \frac{17}{25}$.)

C. 736.Az internetről egy 1,5 MB-os fájlt töltünk le a számítógépünkre. A művelet során a program a letöltés addigi átlagos sebessége alapján folyamatosan megbecsüli a még hátralevő időt. A képernyőre pillantva azt látjuk, hogy a fájlnak pontosan a felét már letöltötte a program, s ekkor a műveletből hátralevő időt pontosan 2 percre becsüli. Ezután bármely t idő elteltével azt tapasztaljuk, hogy (a hálózat leterheltsége miatt) még mindig 2 percet ír ki a program a fájl letöltéséből hátralevő időként. Adjuk meg t függvényeként a fájl már letöltött részének méretét.

Javasolta: Koncz Levente, Budapest

Megoldás. Jelölje g(t) azt, hogy t idő alatt a fájl hányad részét sikerült letölteni. Ekkor - tetszőleges t-re - a még letöltésre váró $\displaystyle \frac{1}{2}-g(t)$ rész és a már letöltött g(t) rész arányának t-szerese azt mutatja, hogy a letöltésből hátralevő idő még mindig 2 perc, azaz

$\displaystyle \frac{\frac{1}{2}-g(t)}{g(t)}\cdot t=2,$

így $\displaystyle g(t)=\frac{t}{2t+4}$, tehát a t idő múlva már letöltött rész mérete a fájl teljes terjedelmének a $\displaystyle g(t)+\frac{1}{2}=\frac{t+1}{t+2}$ része, azaz $\displaystyle \frac{t+1}{t+2}\cdot1.5{\,\,\,MB}$.

C. 737.Egy cukorkát gyártó vállalatnál a legújabb terméket téglatest alakú dobozokba kívánják csomagolni, a 10 dobozból összeálló gyűjtőcsomagokat pedig vékony fóliával burkolni.

Az igazgató szerint előnyös lenne, ha a gyűjtőcsomag geometriailag hasonló volna a cukorkás dobozhoz. Megvalósítható-e az elképzelése?

Megoldás. Az elképzelés megvalósítható, pl. ha a cukorkás doboz oldalai a=1, $\displaystyle b=\root_3\of{10}$, $\displaystyle c=\root_3\of{100}$, akkor a legnagyobb b xc lap mentén 10-es oszlopba csomagolva a csomag b xc x10a-s méretei az eredetihez hasonló téglatestet jelentenek, hiszen $\displaystyle \frac{b}{c}= \frac{\root_3\of{10}}{\root_3\of{100}}=\frac{1}{\root_3\of{10}}= \frac{a}{b}$ és $\displaystyle \frac{c}{10a}=\frac{\root_3\of{100}}{10}= \frac{\root_3\of{10}}{\root_3\of{100}}=\frac{b}{c}$.

C. 738.Milyen nagy lehet egy háromszög területe, ha egyik oldalának a hossza sem nagyobb 2-nél?

Megoldás. A háromszög területe nem csökken, ha akkorára nagyítjuk, hogy a legnagyobb oldala 2 legyen. Jelölje az ehhez tartozó magasságot m, ami az oldalt x és 2-x hosszúságú szakaszokra vágja. Pitagorasz tétele szerint a másik két oldal $\displaystyle \s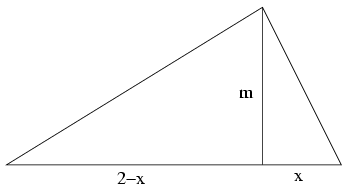qrt{m^2+x^2}\le2$ és $\displaystyle \sqrt{m^2+(2-x)^2}\le2$.

A háromszög akkor megengedett, ha az x² $\displaystyle \le$4 - m² és az x² - 4x + m²$\displaystyle \le$0 egyenlőtlenségeknek van közös x megoldása. Külön-külön az egyenlőtlenségek megoldása: $\displaystyle 0\le x\le\sqrt{4-m^2}$ és $\displaystyle 2-\sqrt{4-m^2} \le x\le2+\sqrt{4-m^2}$. Közös megoldás pontosan akkor létezik, ha $\displaystyle 2-\sqrt{4- m^2}\le\sqrt{4-m^2}$, azaz $\displaystyle m\le\sqrt{3}$. Így a háromszög területe $\displaystyle t=\frac{1}{2}\cdot2m=m\le\sqrt{3}$, és a maximumát akkor veszi fel, ha $\displaystyle m=\sqrt{3}$, x=1, és ekkor a háromszög másik két oldalának hossza is 2 egység.

C. 739.Egy ,,csuklós'' deltoid oldalai 3 cm és 4 cm hosszúak, szögei változtathatók. Mekkora a konvex deltoid átlóinak hossza, ha a területe fele az elérhető legnagyobb értéknek?

Megoldás.

A deltoid területe t=3 ^.4 ^.sin $\displaystyle \alpha$, ezért a terület legnagyobb értéke t_max = 12, ennek fele pedig 6. Ha 6= t = 12 ^.sin $\displaystyle \alpha$, akkor $\displaystyle \sin\alpha=\frac{1}{2}$, így $\displaystyle \alpha$= 30^o vagy 150^o, ezért $\displaystyle \cos\alpha=\pm\frac{\sqrt{3}}{2}$. A koszinusz tétel szerint $\displaystyle e^2=3^2+4^2-2\cdot3\cdot4\cos\alpha=25\pm12\sqrt{3}$.

Azonban ha az $\displaystyle \alpha$=30^o-hoz tartozó e értéket felhasználva kiszámítjuk cos $\displaystyle \beta$-t, azt kapjuk, hogy az negatív, így ebben az esetben a deltoid konkáv lenne.

Az $\displaystyle \alpha$=150^o-hoz tartozó esetben a deltoid biztosan konvex. Átlóinak hossza: $\displaystyle e=\sqrt{25+12\sqrt{3}}$ és $\displaystyle f=\frac{2t}{e}=\frac{12}{\sqrt{25+12\sqrt{3}}}$.