A 2004. októberi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 775. Pistike eredeti módon számlál az ujjain. 1-gyel kezdi a hüvelykujján, ezután a 2-t és a 3-at a mutatóujján, a 4-et, 5-öt és a 6-ot a középső ujján, a 7-et a gyűrűsujján, a 8-at és 9-et a kisujján. Ezután visszafelé folytatja, a 10-et, 11-et, 12-t megint a gyűrűsujján, 13-at a középsőn, 14-et és 15-öt a mutatón, 16-ot, 17-et, 18-at a hüvelykujján, 19-et ismét visszafelé a mutatóujján és így tovább. Melyik ujján számolja a 2004-et?

Megoldás. Az, hogy hányat számol egy ujján, három ujjanként ismétlődik, ezalatt összesen hatot számol Pistike. Annak pedig, hogy melyik ujján számol, 8 a periódusa: hüvelyk, mutató, középső, gyűrűs, kis, gyűrűs, középső, mutató, és innen kezdve ez ismétlődik. Mivel [3,8]=24, ezért a számlálásnak 24 a periódusa, ami alatt ennek kétszeresét, vagyis 48-at számlál Pistike. 2004=42^.48+36. Mivel 36=6^.6, ezért a 2004-et a 3^.6=18. ujján, 18=2^.8+2 vagyis a 2., azaz a mutatóujján számolja.

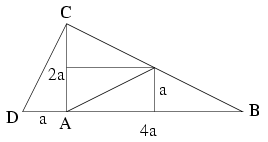
C. 776. Mutassunk példát olyan derékszögű háromszögre, amely felbontható öt egybevágó háromszögre.

Megoldás. Ilyen például a BCD derékszögű háromszög, melyet úgy kaptunk, hogy az ABC derékszögű háromszöget (befogóinak hossza 2a és 4a) középvonalaival felosztottunk 4 darab egybevágó derékszögű háromszögre. Ehhez ragasztottuk hozzá az előzőkkel egybevágó ACD derékszögű háromszöget.

C. 777. Az özönvíz előtti jegykezelő gépek a menetjegy kilenc számozott mezője közül néhányat - akár az összeset - kilyukasztanak. A gépek beállítójától az ellenőrök azt kérik, hogy a gép ne ugyanazokat a mezőket lyukassza, ha valaki nem az előírásnak megfelelően, hanem lapjával fordítva helyezi be a jegyét. Hány ilyen beállítása lehetséges a gépnek?

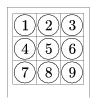
Megoldás. Az 1 és 3 számok közül csak az egyik lehet kilyukasztva, ez 2 lehetőség. A további 7 helyen vagy van lyuk vagy nincs, ez további 2⁷ eset, vagyis összesen: 2^.2⁷.

Ugyanígy vizsgáljuk meg a 4 és 6 számok lyukasztásának lehetőségeit, ez 2^.2⁵, hozzávéve az 1, 3 lehetőségeit ez összesen: 2^.2^.2⁵. Végül a 7 és 9 számokra 2^.2^.2^.2³ a lehetséges esetek száma. Ezeket összegezve:

2^.2⁷+2^.2^.2⁵+2^.2^.2^.2³=2⁸+2⁷+2⁶=448.

C. 778. Egy számtani sorozatban jelölje S_m a sorozat első m elemének az összegét. Bizonyítsuk be, hogy minden n>k$\displaystyle \ge$1 esetén

$\displaystyle \frac{S_{n+k}}{n+k}=\frac{S_n-S_k}{n-k}.$

Megoldás. Írjuk fel a számtani sorozat ismert összegképletét.

$\displaystyle S_{n+k}={n+k\over2}\left(a_1+a_{n+k}\right)={n+k\over2}\left(2a_1+(n+k-1)d\right).$

Mivel n>k, ezért

$\displaystyle S_{n}-S_k={n-k\over2}\left(a_{k+1}+a_{n}\right)={n-k\over2}\left(2a_1+kd+(n-1)d\right).$

Innen a feladat állítása már nyilván adódik.

C. 779. Egy 12x12x35 cm-es, 5 kg tömegű gépsonkát ferdén vágtunk el úgy, hogy a paralelogramma alakú metszet oldalhosszúsága 15 és 20 cm. Mekkora lehet a keletkezett két darab tömege?

Megoldás.

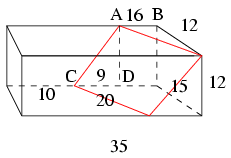
$\displaystyle AB=\sqrt{20^2-12^2}=16,$

$\displaystyle CD=\sqrt{15^2-12^2}=9.$

A levágás után maradt egy 12x12x10 cm³-es hasáb és egy ugyanolyan rész, mint amilyet levágtunk. A hasáb tömege $\displaystyle {5000\cdot1440\over5040}\approx1428,57$ g $\displaystyle \approx$1,429 kg. A levágott rész tömege (ha a vágást a csúcsnál kezdjük) $\displaystyle {5-1,429\over2}\approx1,786$ kg, ekkor a legkisebb és legfeljebb 5-1786=3,214 kg.