A 2005. januári C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 790. Egy konkáv négyszög oldalainak felezőpontjait összekötöttük az ábrán látható módon. Hogyan aránylik az így kapott négyszög területe az eredeti négyszög területéhez?

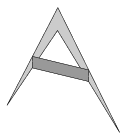
Megoldás. A négyszög csúcsai A, B, C és D, a felezőpontok pedig F₁, F₂, F₃ és F₄.

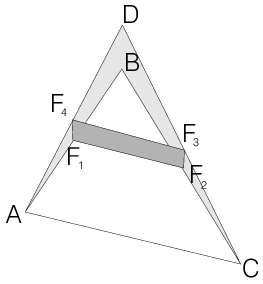
Látható, hogy \(\displaystyle t_{F_1F_2F_3F_4}=t_{ACD}-\left(t_{DF_4F_3}+t_{AF_1F_4}+t_{F_3F_2C}+t_{ACF_2F_1}\right)\). Legyen \(\displaystyle t_{F_1F_2F_3F_4}=t\), t_ABD=t₁, t_DBC=t₂ és t_ACB=t₃. Fejezzük ki a bevezetett ismeretlenek segítségével a kérdéses területet. Tudjuk, hogy t_ACD=t₁+t₂+t₃. Az F₃F₄ az ACD háromszögben középvonal, így a DF₃F₄ és az ACD háromszögek hasonlóak, a hasonlóság aránya 1:2, emiatt \(\displaystyle t_{DF_4F_3}={t_1+t_2+t_3\over4}\). Az F₁F₂ az ABC háromszög középvonala, a hasonlóság miatt itt \(\displaystyle t_{ACF_2F_1}={3t_3\over4}\). Az ABD háromszögben F₁F₄, továbbá a BCD háromszögben F₂F₃ szintén középvonalak, ebből adódóan \(\displaystyle t_{AF_1F_4}={t_1\over4}\) és \(\displaystyle t_{CF_3F_2}={t_2\over4}\). Ekkor a keresett terület: \(\displaystyle t=t_1+t_2+t_3-\left({t_1+t_2+t_3\over4}+{t_1\over4}+{t_2\over4}+{3t_3\over4}\right)={t_1+t_2\over2}.\) Mivel t₁+t₂=t_ABCD, ezért \(\displaystyle t={t_{ABCD}\over2}\).

Azaz a felezőpontok által meghatározott négyszög területének és az eredeti konkáv négyszög területének az aránya: 1 : 2.

C. 791. Egy 9-szer 9-es táblázat mezőibe 460-tól 540-ig beírtuk egymás után az egész számokat a bal felső sarokból indulva, soronként balról jobbra haladva. Elhelyezhető-e ezen a táblán egy négy négyzetből álló, L betűt formázó kartonlap úgy, hogy 4 olyan számot fedjen le, amelyek összege 2005?

Megoldás. Színezzük be a táblázat mezőit sakktáblaszerűen, a páros számot tartalmazó mezők legyenek feketék, a páratlanok fehérek. Egy L-alakzatot akármilyen irányban helyezünk is el a táblán, az két fekete és két fehér mezőt fog takarni. Az L-alakzatban lévő négy szám összege két páros és két páratlan szám összege lesz. Ez az érték azonban mindig páros, tehát nem lehet 2005. Vagyis nem helyezhető el a táblán a feltételeknek megfelelően a kartonlap.

C. 792. Oldjuk meg a következő egyenlőtlenséget:

\(\displaystyle \sqrt{x^2+x}+x<\frac{1}{2}. \)

Megoldás. Írjuk az egyenlőtlenséget \(\displaystyle \sqrt{x^2+x}<{1\over2}-x\) alakban! A bal oldal csak akkor értelmezhető, ha x\(\displaystyle \le\)-1 vagy 0\(\displaystyle \le\)x. Mivel a bal oldal nemnegatív, ezért a jobb oldalra \(\displaystyle 0<{1\over2}-x\), ebből \(\displaystyle x<{1\over2}\), tehát \(\displaystyle x\in]-\infty;-1]\cup\left[0;{1\over2}\right[\). Mivel a \(\displaystyle \sqrt{x^2+x}<{1\over2}-x\) egyenlőtlenség mindkét oldala nemnegatív, ezért négyzetre emelhetünk, ekkor \(\displaystyle x^2+x

C. 793. Mennyi

\(\displaystyle \sqrt[4010]{\frac{1}{2}\big(19+6\sqrt{10}\,\big)}\cdot\sqrt[2005]{3\sqrt{2}- 2\sqrt{5}} \)

pontos értéke?

Megoldás. A kifejezés előjele negatív, mivel a szorzat második tényezőjében \(\displaystyle 3\sqrt2-2\sqrt5\) értéke negatív, így ennek páratlan gyökkitevőjű értéke is negatív lesz. (A szorzat első tényezőjében a gyökjel alatti kifejezés pozitív, ennek páros gyökkitevőjű gyöke is pozitív.) Írjuk át a kifejezést: \(\displaystyle (-1)\cdot\root{4010}\of{{1\over2}(19+6\sqrt{10})}\cdot\root{2005}\of{2\sqrt5-3\sqrt2}\). Mivel \(\displaystyle 2\sqrt5-3\sqrt2\) már pozitív, ezért \(\displaystyle \root{2005}\of{2\sqrt5-3\sqrt2}\) felírható \(\displaystyle \root{4010}\of{(2\sqrt5-3\sqrt2)^2}\) alakban. Tudjuk, hogy , \(\displaystyle \root{4010}\of{(2\sqrt5-3\sqrt2)^2}=\root{4010}\of{38-12\sqrt{10}}\), ezért így írhatjuk tovább:

\(\displaystyle (-1)\cdot\root{4010}\of{(19+6\sqrt{10})\cdot{1\over2}\cdot(38-12\sqrt{10})}=(-1)\cdot\root{4010}\of{(19+6\sqrt{10})\cdot(19-6\sqrt{10})}.\)

Az (a+b)(a-b)=a²-b² azonosságot alkalmazva kapjuk, hogy

\(\displaystyle (-1)\cdot\root{4010}\of{19^2-(6\sqrt{10})^2}=(-1)\cdot\root{4010}\of{1}=-1.\)

Tehát a kifejezés pontos értéke: -1.

C. 794. Egy gömb két párhuzamos síkmetszetének területe 9\(\displaystyle \pi\) és 16\(\displaystyle \pi\). A síkok távolsága egységnyi. Mekkora a gömb felszíne?

Megoldás. A két párhuzamos síkmetszet egy-egy kör, amelyek területe t₁=9\(\displaystyle \pi\) és t₂=16\(\displaystyle \pi\), ezért a két kör sugara r₁=3 és r₂=4 egység.

Készítsünk keresztmetszeti rajzot a gömbről!

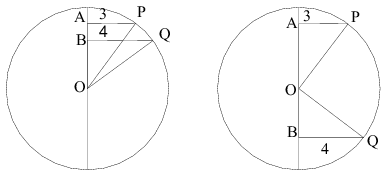
1. ábra                                          2. ábra

Az ábráknak megfelelően két esetet kell megkülönböztetnünk aszerint, hogy az A és B pontok az O azonos vagy különböző oldalára esnek az általuk meghatározott egyenesen. Mindkét ábrán OP=OQ=r, ahol r a gömb sugarát jelöli; AB=1, és legyen BO=x. Az AOP és BOQ háromszögek derékszögűek, így a Pitagorasz-tételből OA²+AP²=OP² és OB²+BQ²=OQ², tehát OP=OQ miatt OA²+AP²=OB²+BQ². Ekkor felírhatjuk az alábbi egyenleteket:

1. eset: OA=x+1, tehát (x+1)²+3²=x²+4², ebből x=3 és r=5.

2. eset: OA=1-x, tehát (1-x)²+3²=x²+4², ebből x=-3, vagyis A és B nem eshet az O különböző oldalára az általuk meghatározott egyenesen.

Vagyis a gömb felszíne: A=4r²\(\displaystyle \pi\)=100\(\displaystyle \pi\) (területegység).