Az A. 496. feladat (2009. december)

A. 496. Legyenek a₁,a₂,...,a_2k páronként különböző egész számok, és legyen M legfeljebb k elemű, egész számokból álló halmaz, ami nem tartalmazza sem a 0, sem az s=a₁+a₂+...+a_2k számot. Egy szöcske a valós számegyenesen ugrál a 0 pontból kiindulva úgy, hogy 2k ugrást hajt végre, melyek nagysága a₁,a₂,...,a_2k valamilyen sorrendben. Ha a_i>0, akkor a megfelelő lépésben a szöcske jobb kéz felé, ha pedig a_i<0, akkor bal kéz felé ugrik |a_i| távolságra. Bizonyítsuk be, hogy a szöcske meg tudja választani az ugrások sorrendjét úgy, hogy ne ugorjon az M halmaz egyik elemére se.

(5 pont)

A beküldési határidő 2010. január 11-én LEJÁRT.

Megoldás. S_n-nel fogjuk jelölni az (1,2,...,n) indexek permutációinak csoportját. Minden egyes $\pi$ $\in$ S_n-re $\mathrm{sgn}(\pi)$ jelöli a $\pi$ permutáció előjelét, ami páros permutációra +1, páratlan permutációra -1.

Legyen

$P(x_1,\ldots,x_n) = \sum_{\pi\in S_{2k}} \sgn(\pi) \prod_{\ell=1}^{2k-1} \prod_{m\in M} \big((x_{\pi(1)}+x_{\pi(2)}+\ldots+x_{\pi(\ell)})-m\big),$

(1)

és tekintsük a $P(a_1,\ldots,a_{2k})$ számot.

Ha $P(a_1,\ldots,a_{2k})\ne0$ , akkor létezik legalább egy olyan $\pi$ $\in$ S_2k permutáció, amire

$\prod_{\ell=1}^{2k-1} \prod_{m\in M} \big((x_{\pi(1)}+x_{\pi(2)}+\ldots+x_{\pi(\ell)})-m\big) \ne 0.$

Ez utóbbi viszont akkor és csak akkor nem 0, ha az $a_{\pi(1)}$ , $(a_{\pi(1)}+a_{\pi(2)})$ , ..., $(a_{\pi(1)}+a_{\pi(2)}+\dots+a_{\pi(2k-1)})$ számok különböznek az összes M-beli számtól; más szóval akkor, ha a szöcske végig tud ugrálni a 0, $a_{\pi(1)}$ , $a_{\pi(1)}+a_{\pi(2)}$ , ..., $a_{\pi(1)}+a_{\pi(2)}$ , ..., $a_{\pi(1)}+\ldots+a_{\pi(2k-1)}$ , s számokon. Célunk tehát annak igazolása, hogy $P(a_1,\ldots,a_{2k})\ne0$ .

A P polinom alternáló, vagyis bármelyik két változó felcserélésével a polinom (-1)-szeresét kapjuk, és ha bármelyik két változó helyére ugyanazt az értéket helyettesítjük, a polinom értéke 0 lesz. Jól ismert, hogy minden alternáló polinom, tehát P is, töbszöröse a

$V(x_1,\ldots,x_{2k}) = \prod\limits_{1\le i<j\le2k}(x_j-x_i) = \sum_{\pi\in S_{2k}} \sgn(\pi) \, x_{\pi(2) }x_{\pi(3)}^2\cdots x_{\pi(2k)}^{2k-1}$

úgynevezett Vandermonde-polinomnak. A P foka legfeljebb k(2k-1), ami megegyezik a $V(x_1,x_2,\ldots,x_{2k})$ Vandermonde-polinom fokával. A P tehát konstansszorosa a Vandermonde-polinomnak:

$P(x_1,x_2,\ldots,x_{2k}) = (-1)^k c_k \cdot V(x_1,x_2,\ldots,x_{2k}).$

(A (-1)^k előjel egy kis magyarázatra szorul. A $\prod\limits_{\ell=1}^{2k-1} \prod\limits_{m\in M} \big((x_1+x_2+\ldots+x_\ell)-m\big)$ szorzatban a Vandermonde-polinom tagjai közül az x₁^2k-1x₂^2k-2^...x_2k-1 szerepel a legtöbbször; a Vandermonde-polinomban ennek a tagnak az együtthatója (-1)^k.)

Észrevehetjük, hogy a P polinom, és vele együtt a c_k szám egyáltalán nem függ az M halmaztól. Ezért ugyanazzal a c_k konstanssal az is igaz, hogy

$P(x_1,\ldots,x_{2k}) = \sum_{\pi\in S_{2k}} \sgn(\pi) \prod_{\ell=1}^{2k-1} \big(x_{\pi(1)}+x_{\pi(2)}+\ldots+x_{\pi(\ell)}\big)^k = (-1)^k c_k \cdot V(x_1,x_2,\ldots,x_{2k}).$

(2)

Az ugrásokat behelyettesítve,

$P(a_1,a_2,\ldots,a_{2k}) = (-1)^k c_k \cdot V(a_1,a_2,\ldots,a_{2k}).$

Mvel az $a_1,\ldots,a_{2k}$ ugrások különbözőek, $V(a_1,a_2,\ldots,a_{2k})\ne0$ . A feladat megoldásához már csak annyi hiányzik, hogy c_k $\ne$ 0, avagy, (1) jobboldala nem esik ki szőröstül-bőröstül.

A c_k $\ne$ 0 állításnál többet bizonyítunk.

Definíció. Legyen tetszőleges u,v $\ge$ 0 egészekre

$P^{(n,u,v)}(x_1\ldots,x_n) = \sum_{\pi\in S_n} \sgn(\pi) \left( \prod_{\ell=1}^{n-1} \big(x_{\pi(1)}+x_{\pi(2)}+\ldots+x_{\pi(\ell)}\big)^u \right) (x_1+\ldots+x_n)^v.$

(3)

Tetszőleges $d_1>\ldots>d_n\ge0$ egészekre jelöljük $\alpha^{(n,u,v)}_{d_1,\ldots,d_n}$ -nel x₁^d₁^...x_n^d_n együtthatóját a P^(n,u,v) polinomban. Mivel a polinom alternáló,

$P^{(n,u,v)}(x_1,\ldots,x_n) = \sum_{d_1>\ldots>d_n\ge0} \alpha^{(n,u,v)}_{d_1,\ldots,d_n} \sum_{\pi\in S_n} \sgn(\pi) \, x_{\pi(1)}^{d_1} x_{\pi(2)}^{d_2} \cdots x_{\pi(n)}^{d_n}.$

(4)

Az egyszerűség kedvéért az $\alpha^{(n,u,v)}_{d_1,\ldots,d_n}$ együtthatót akkor is definiáljuk, ha d_i=d_i+1 valamelyik 1 $\le$ i<n indexre, vagy ha d_n<0; ilyenkor $\alpha^{(n,u,v)}_{d_1,\ldots,d_n}=0$ .

1. lemma. n $\ge$ 2 esetén

(a) tetszőleges $d_1>\ldots>d_n>0$ sorozatra

$\alpha^{(n,u,0)}_{d_1,\ldots,d_n} = 0$

és

(b) tetszőleges $d_1>\ldots>d_{n-1}>0$ sorozatra

$\alpha^{(n,u,0)}_{d_1,\ldots,d_{n-1},0} = \alpha^{(n-1,u,u)}_{d_1,\ldots,d_{n-1}}.$

Bizonyítás. Tekintsük a

$P^{(n,u,0)}(x_1,\ldots,x_n) = \sum_{\pi\in S_n} \sgn(\pi) \prod_{\ell=1}^{n-1} \big(x_{\pi(1)}+x_{\pi(2)}+\ldots+x_{\pi(\ell)}\big)^u =$

$= \sum_{d_1>\ldots>d_{n-1}>0} \alpha^{(n,u,0)}_{d_1,\ldots,d_{n-1},0} \sum_{\pi\in S_n} \sgn(\pi) \, x_{\pi(1)}^{d_1} x_{\pi(2)}^{d_2} \cdots x_{\pi(n-1)}^{d_{n-1}}$

polinomot.

A baloldalon a $\prod_{\ell=1}^{n-1} \big(x_{\pi(1)}+x_{\pi(2)}+\ldots+x_{\pi(\ell)}\big)^u$ szorzatban nem szerepel az $x_{\pi(n)}$ változó. Ezért x₁^d₁x₂^d₂^...x_n-1^d_n-1 alakú tagot csak az olyan permutációkra kaphatunk, amikben $\pi$ (n)=n. Az ilyen permutációkra összegezve pedig

$\sum_{\pi\in S_n,\,\pi(n)=n} \sgn(\pi) \prod_{\ell=1}^{n-1} \big(x_{\pi(1)}+x_{\pi(2)}+\ldots+x_{\pi(\ell)}\big)^u = P^{(n-1,u,u)}(x_1,\ldots,x_{n-1}).$

Tehát x₁^d₁x₂^d₂^...x_n-1^d_n-1 együtthatója a P^(n,u,0) polinomban ugyanaz, mint a P^(n-1,u,u) polinomban.

2. lemma. Ha v $\ge$ 1, akkor tetszőleges $d_1>\ldots>d_n\ge0$ sorozatra

$\alpha^{(n,u,v)}_{d_1,\ldots,d_n} = \sum_{i=1}^n \alpha^{(n,u,v-1)}_{d_1,\ldots,d_{i-1},d_i-1,d_{i+1},\ldots,d_n}.$

Bizonyítás. A P^(n,u,v) definiója alapján

$P^{(n,u,v)}(x_1,\ldots,x_n) = P^{(n,u,v-1)}(x_1,\ldots,x_n) \cdot (x_1+\ldots+x_n) = \sum_{i=1}^n P^{(n,u,v-1)}(x_1,\ldots,x_n) \cdot x_i.$

Az x₁^d₁x₂^d₂^...x_n^d_n együtthatója a baloldalon $\alpha^{(n,u,v)}_{d_1,\ldots,d_n}$ , a jobboldalon az $P^{(n,u,v-1)}(x_1,\ldots,x_n) \cdot x_i$ polinomban pedig $\alpha^{(n,u,v-1)}_{d_1,\ldots,d_{i-1},d_i-1,d_{i+1},\ldots,d_n}$ .

3. lemma. Tetszőleges n $\ge$ 1, u,v $\ge$ 0 és $d_1\ge\ldots\ge d_n\ge0$ egész számokra

$\alpha^{(n,u,v)}_{d_1,\ldots,d_n}\ge0.$

Bizonyítás. Indukció. n=1 esetén P^(1,u,v)(x₁)=x₁^v, az egyetlen együttható pozitív. Innen, az 1. és 2. lemmát alkalmazva, triviális.

4. lemma. Legyenek n $\ge$ 1, u $\ge$ n/2 és v $\ge$ 0 egészek. Ekkor $\alpha^{(n,u,v)}_{d_1,\ldots,d_n}>0$ minden olyan, egészekből álló $d_1>\ldots>d_n\ge0$ sorozatra, amelyben $d_1+\ldots+d_n=(n-1)u+v$ és d_n $\le$ v.

Bizonyítás. Teljes indukcióval bizonyítunk.

Az n=1 esetben P^(1,u,v)(x₁)=x₁^v, és az egyetlen együttható 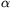$\alpha$ ^(1,u,v)_v=1>0. A továbbiakban feltételezzük, hogy n>1, és az állítás igaz minden olyan esetben, amikor

(a) n-et kisebbre cseréljük, vagy pedig

(b) v értékét csökkentjük, miközben n értéke változatlan marad.

1. eset: v=0. A d_n $\le$ v feltétel miatt csak d_n=0 lehetséges. Az 1. lemma szerint

$\alpha^{(n,u,0)}_{d_1,\ldots,d_{n-1},0} = \alpha^{(n-1,u,u)}_{d_1,\ldots,d_{n-1}}.$

Az indukciós feltételt az (n',u',v')=(n-1,u,u) hármasra és az $(d'_1,\ldots,d'_{n-1})=(d_1,\ldots,d_{n-1})$ számokra alkalmazzuk.

Az $u'>\frac{n'}2$ feltétel teljesül, mert $u'=u\ge\frac{n}2>\frac{n'}2$ .

Mivel v=d_n=0,

$d'_1+d'_2+\ldots+d'_{n'} = d_1+d_2+\ldots+d_{n-1}+d_n = (n-1)u = (n'-1)u' + v'.$

Végül,

$d'_{n'} = d_{n-1} \le \frac{d_1+d_2+\ldots+d_{n-1}}{n-1} = u = v'.$

A lemma feltételei tehát mind teljesülnek, és $\alpha^{(n,u,0)}_{d_1,\ldots,d_{n-1},0} = \alpha^{(n-1,u,u)}_{d_1,\ldots,d_{n-1}}>0$ .

2. eset: v>0. Az indukciós feltevést most az (n',u',v')=(n,u,v-1) hármasra alkalmazzuk, mert a 2. lemma szerint

$\alpha^{(n,u,v)}_{d_1,\ldots,d_n} = \sum_{i=1}^n \alpha^{(n,u,v-1)}_{d_1,\ldots,d_{i-1},d_i-1,d_{i+1},\ldots,d_n}.$

A 3. lemma szerint a jobboldalon csupa nemnegatív szám áll; azt kell megmutatnunk, hogy van közöttük legalább egy pozitív is.

Mivel

$d_1+\ldots+d_n = (n-1)u+v > (n-1)\cdot\frac{n}2+0 = (n-1)+(n-2)+\ldots+1+0,$

létezik legalább egy olyan 1 $\le$ i $\le$ n index, amire d_i>n-i. Tekintsük az utolsó ilyen indexet. Ha i<n, akkor d_i-1>d_i+1; ha pedig i=n, akkor d_n-1 $\ge$ 0.

Alkalmazzuk az indukciós feltevést az $(d'_1,\ldots,d'_n)=(d_1,\ldots,d_{i_0-1},d_{i_0}-1,d_{i_0+1},\ldots,d_n)$ számokra. Az i választásából következik, hogy $d'_1>\ldots>d'_n\ge0$ .

Az $u'\ge\frac{n'}2$ feltétel triviálisan teljesül.

Végül, d'_n=max (d_n-1,0) $\le$ v-1 miatt az igaz, hogy d'_n $\le$ v.

Az indukciós feltevés tehát az $\alpha^{(n-1,u,u)}_{d_1,\ldots,d_{i-1},d_{i}-1,d_{i+1},\ldots,d_n}$ számok közül legalább egyre alkalmazható.

Ezzel a Lemmát igazoltuk.

Következmény. c_k>0 minden egyes pozitív egész k-ra.

Bizonyítás. Alkalmazzuk a 4. lemmát az n=2k, u=k, v=0, $(d_1,\dots,d_{2k})=(2k-1,2k-2,\ldots,1,0)$ számokra. A lemma feltételei teljesülnek, ezért

$c_k = \alpha^{(2k,k,0)}_{2k-1,2k-2,\ldots,1,0} > 0.$

Statisztika:

2 dolgozat érkezett.

4 pontot kapott: Nagy 235 János.

3 pontot kapott: 1 versenyző.

A KöMaL 2009. decemberi matematika feladatai

2 dolgozat érkezett.
4 pontot kapott:	Nagy 235 János.
3 pontot kapott:	1 versenyző.

Már regisztráltál?
Új vendég vagy?