Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány

Már regisztráltál?
Új vendég vagy?

A B. 4465. feladat (2012. szeptember)

B. 4465. Az A₀A₁₀ szakaszt felosztottuk 10 egyenlő részre. Az osztópontok rendre $A_{1}, A_{2}, \ldots, A_{9}$ . Az A₈A₁₀ szakaszra emelt szabályos háromszög harmadik csúcsa legyen B. Mutassuk meg, hogy

$BA_{0}A_{10}\sphericalangle + BA_{2}A_{10}\sphericalangle + BA_{3}A_{10}\sphericalangle +BA_{4}A_{10}\sphericalangle =60^{\circ}.$

Javasolta: Miklós Szilárd (Herceghalom)

(4 pont)

A beküldési határidő 2012. október 10-én LEJÁRT.

Megoldás. Legyen az A₀A₁ szakasz hossza egységnyi, ekkor az A₈A₁₀B háromszög B-ből induló magassága $A_9B=\sqrt{3}$ . A szóban forgó szögeket jelölje rendre 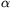$\alpha$ , $\beta$ , $\gamma$ , $\delta$ . Ekkor $\tg\alpha=\sqrt{3}/9, \tg\beta=\sqrt{3}/7, \tg\gamma=\sqrt{3}/6, \tg\delta=\sqrt{3}/5$ . Az összegképlet szerint

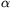$\tg(\alpha+\delta)=\frac{\tg\alpha+\tg\delta}{1-\tg\alpha\tg\delta}= \frac{\sqrt{3}}{3}=\frac{\tg\beta+\tg\gamma}{1-\tg\beta\tg\gamma}= \tg(\beta+\gamma),$

vagyis $\alpha$ + $\delta$ = $\beta$ + $\gamma$ =30^o. A négy szög összege tehát valóban 60^o.

Statisztika:

207 dolgozat érkezett.

4 pontot kapott: 118 versenyző.

3 pontot kapott: 3 versenyző.

1 pontot kapott: 83 versenyző.

0 pontot kapott: 3 versenyző.

A KöMaL 2012. szeptemberi matematika feladatai

207 dolgozat érkezett.
4 pontot kapott:	118 versenyző.
3 pontot kapott:	3 versenyző.
1 pontot kapott:	83 versenyző.
0 pontot kapott:	3 versenyző.