 |
Az S. 70. feladat (2012. március) |
S. 70. Béla szereti mindig jól átlátni a környezetét, így miután Nevesincs városba költözött, első dolga az volt, hogy rajzolt egy térképet a városról, és följegyezte rajta minden egyes utca hosszát -- természetesen mikrométerben, mivel a pontatlanságot ki nem állhatja. Ezek után persze az útvonalait is nagyon gondosan tervezi meg: most például azt eszelte ki, hogy úgy jusson el A-ból B-be, hogy az útvonalán előforduló leghosszabb és legrövidebb utca hosszának különbsége minimális legyen. Írjunk programot, amely meghatároz Béla számára egy ilyen tulajdonságú útvonalat.
A program a város leírását a standard bemenetről olvassa. Ennek első sorában egyetlen szóközzel elválasztva a kereszteződések N száma, illetve az ezeket összekötő utcák M száma található (1 N
N 1000, 0
1000, 0 M
M 5000). A második sor az A és B kereszteződések sorszámát tartalmazza, az ezt követő M darab sor pedig rendre egy-egy utcát ír le XiYiLi formátumban, ahol Xi és Yi az i-edik utca által összekötött két kereszteződés sorszáma, Li pedig az i-edik utca hossza (1
5000). A második sor az A és B kereszteződések sorszámát tartalmazza, az ezt követő M darab sor pedig rendre egy-egy utcát ír le XiYiLi formátumban, ahol Xi és Yi az i-edik utca által összekötött két kereszteződés sorszáma, Li pedig az i-edik utca hossza (1 Li
Li 109). Feltehetjük, hogy egy utca két végpontja mindig különbözik egymástól, valamint hogy nincs két olyan utca, melyek mindkét végpontja megegyezik. A kereszteződéseket 0-tól N-1-ig sorszámozzuk.
109). Feltehetjük, hogy egy utca két végpontja mindig különbözik egymástól, valamint hogy nincs két olyan utca, melyek mindkét végpontja megegyezik. A kereszteződéseket 0-tól N-1-ig sorszámozzuk.
A standard kimenet egyetlen sorába egy darab szám kerüljön: ha elérhető A-ból B, akkor az elérhető legkisebb különbség, ellenkező esetben pedig -1.

A maximális pontszám eléréséhez a programnak a legnagyobb teszteseteket is legfeljebb 1 másodperc alatt meg kell oldania.
Beküldendő egy tömörített s70.zip állományban a program forráskódja (s70.pas, s70.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s70.txt, s70.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrás melyik fejlesztőkörnyezetben fordítható.
(10 pont)
A beküldési határidő 2012. április 10-én LEJÁRT.
A bemenetben megadott kereszteződéseket és utcákat tekinthetjük egy gráf csúcsainak és éleinek, ahol az élek meg vannak címkézve az utca hosszával. Ekkor az a feladat, hogy keressünk a két megadott csúcs között egy olyan utat, amelyen a legrövidebb és a leghosszabb él különbsége minimális.
Backtrack
Egy egyszerű (de lassú) megoldás, hogy visszalépéses kereséssel meghatározzuk az összes lehetséges útvonalat A-ból B-be, közben mindegyikre kiszámoljuk a legrövidebb és a leghosszabb él különbségét, és ezeken végzünk egy minimumkeresést. Ez a megoldás körülbelül 20-as csúcsszámig fut le időben. Hibátlan megvalósítása (megfelelő dokumentációval együtt) 5 pontot ért.
Ötlet
A jobb megoldások alapötlete, hogy rendezzük az éleket hosszuk szerint. Ekkor a feladat a következő: egy olyan intervallumot keresünk a rendezett sorozaton, amelyre igaz, hogy az A csúcsból elérhető a B csúcs csak az intervallum beli éleket használva, és az intervallum kezdő és végpontjában lévő élek hosszának különbsége minimális.
Köbös megoldás
Ebből máris adódik egy olyan megoldás, aminek a futásideje az élek számának köbével arányos. Nézzük végig az összes lehetséges intervallumot (ez idáig O(M2)), és mindegyikre döntsük el, hogy van-e csak a benne lévő éleket használó A->B út (ez egy O(M)-es szorzó a futásidőn). Ez az algoritmus azonban nem fér bele az 1 másodperces futási időlimitbe.
Minimális feszítőfát használó megoldások
Vegyük észre, hogy ha adott az intervallum alsó széle, akkor az (itt kezdődő intervallumok közül) optimális felső szél megtalálása majdnem a minimális feszítőfa problémája azon a gráfon, ami abban különbözik az eredetitől, hogy elhagytuk az alsó szélnél kisebb súlyú éleket. A különbség csak annyi, hogy itt fa helyett elég egy olyan élhalmaz, amit használva létezik A->B út, és a minimalitási feltétel összeg helyett a maximális súlyú élre vonatkozik. A Kruskal és a Prim algoritmus is könnyen módosítható erre a célra, ugyanis mindkettőnél csak annyit kell tenni, hogy megállunk akkor, amikor a feldolgozott éleken már elérhető A-ból B (a minimális összsúlyú feszítőfa mindenképpen rendelkezik a minimális maximális súlyú él tulajdonsággal is (egyébként fordítva ez nem igaz)).
Vagyis ha meghatározzuk az összes élre, hogy mennyi a hozzá tartozó optimális felső határ, és ezeken végzünk egy minimumkeresést, akkor megkapjuk a megoldást. A futásidő O(M2log M) a Prim algoritmus esetén. A Kruskal algoritmust a union-find nevű adatszerkezettel megvalósítva a futasidő O(M2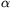 (M)) (a rendezés miatti log M-es szorzó azért nem jelenik meg, mert elég egyszer rendezni az elején), amit tekinthetünk gyakorlati szempontból O(M2)-nek.
(M)) (a rendezés miatti log M-es szorzó azért nem jelenik meg, mert elég egyszer rendezni az elején), amit tekinthetünk gyakorlati szempontból O(M2)-nek.
Az implementáció: S70KruskalUnionFind.cpp
Mivel minimális összsúlyú feszítőfa helyett most a legnagyobb súlyú él minimalizálása a cél, ezért alkalmazhatunk bináris keresést is az optimális felső szél keresésekor (a fölfelé vagy lefelé lépés döntését egy bejárással végezzük). Ennek bemutatására Szabó Attila megoldását közöljük: S70SzaboAttila.zip
Intervallum-léptetés
Strenner Péter megoldása nem használja a minimális feszítőfa fogalmát, hanem egy másik, nagyon tanulságos módszert alkalmaz: Legyen kezdetben az [x, y] intervallum csak az első élt tartalmazó intervallum. Minden lépésben megnézzük, hogy elérhető-e A-ból B csak az [x, y] beli éleken (ahol x és y élek sorszáma a hossz szerinti rendezésben), és ha igen, akkor az x-et növeljük, különben az y-t. Az így előforduló intervallumok közül a legrövidebbnek a hossza a megoldás. A futasidő O(M2), mivel az intervallum eleje és vége is legföljebb M-szer lép, és lépésenként egy O(M)-es bejárást végzünk.
Ugyanez C++-ban implementálva: S70IntervallumLeptetes.cpp
Egyébként ezzel a módszerrel lehet megoldani pl. a 2008-2009-es OKTV 3. korcsoport 3. forduló 1. feladatát is.
O(M log M)
Ugyan az O(M2)-es megoldások beleférnek az 1 másodperces futási időlimitbe, de létezik egy még gyorsabb megoldás is: ugyanazt csináljuk, mint az intervallum-léptetős, csak az A->B elérhetőséget ezzel az adatstruktúrával tartjuk számon: Link/cut tree
Statisztika:
12 dolgozat érkezett. 10 pontot kapott: Strenner Péter, Szabó 928 Attila. 8 pontot kapott: 3 versenyző. 7 pontot kapott: 1 versenyző. 6 pontot kapott: 1 versenyző. 5 pontot kapott: 3 versenyző. 4 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2012. márciusi informatika feladatai
|
|

