A 35. Nemzetközi Fizikai Diákolimpia elméleti feladatai

A részpontszámokat azok kedvéért közöljük, akik - későbbi versenyekre készülve - az olimpiához hasonló feltételek mellett önállóan akarják megoldani a feladatokat. A ,,hivatalos'' megoldást és a mérési feladatot a KöMaL novemberi számában ismertetjük.

A feladatok kidolgozására 5 óra állt rendelkezésre.

1. feladat. ,,Pingpong-ellenállás''

Egy síkkondenzátor két kör alakú, párhuzamos lemezből áll, mindkettő sugara R, a közöttük lévő távolság d, ahol d $\displaystyle \ll$ R (1.(a). ábra). A felső lemez egy állandó feszültségforráshoz csatlakozik, amelynek potenciálja V, míg az alsó lemez földelt. Az alsó lemez közepére egy vékony, kicsiny, m tömegű korongot helyezünk, melynek sugara r ( $\displaystyle \ll$ R, d), vastagsága t ( $\displaystyle \ll$ r), (1.(b). ábra).

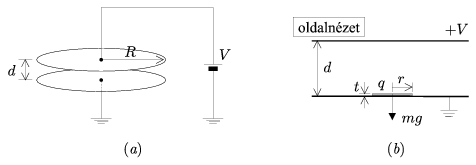
1. ábra. (a): Állandó feszültségforráshoz csatlakozó síkkondenzátor vázlatos rajza. (b) A párhuzamos lemezek oldalnézete a kondenzátorba helyezett kisméretű koronggal

Tételezzük fel, hogy a lemezek közötti térrészben vákuum van, amit az $\displaystyle \varepsilon$ ₀ dielektromos állandó jellemez, továbbá a lemezek és a korong tökéletes vezetőanyagból készültek, illetve mindenféle elektrosztatikus él-effektust elhanyagolhatunk. Az egész áramkör induktivitásától és a relativisztikus hatásoktól szintén eltekinthetünk. A tükörtöltés hatásokat is elhanyagolhatjuk.

(a) (1,2 pont) Határozd meg az egymástól d távolságra lévő lemezek között ható F_p elektrosztatikus erőt, mielőtt a korongot a kettő közé helyeztük, amint ezt az 1.(a). ábra mutatja.

(b) (0,8 pont) Az 1.(b). ábrán lévő kicsiny korong q töltése a következő módon adható meg a felső lemez feszültségének függvényében: $\displaystyle q=\chi V$ . Határozd meg a $\displaystyle \chi$ paramétert r, d és $\displaystyle \varepsilon$ ₀ függvényében!

(c) (0,5 pont) A síkkondenzátor lemezei a g homogén gravitációs térre merőlegesen helyezkednek el. A kezdetben nyugalomban lévő korong megemeléséhez egy bizonyos V_k küszöbérték fölé kell növelnünk az alkalmazott feszültséget. Fejezd ki V_k-t m, g, d és $\displaystyle \chi$ segítségével!

(d) (2,3 pont) Ha V > V_k, a korong föl-le fog mozogni a lemezek között. (Tételezzük fel, hogy a korong mindenféle billegés nélkül, kizárólag függőlegesen mozog.) A korong és a lemezek közötti ütközések részben rugalmatlanok, amit az $\displaystyle \eta$ ütközési számmal jellemezhetünk: $\displaystyle \eta\equiv\frac{v_{előtt}}{v_{után}}$ , ahol v_előtt és v_után rendre a korong sebessége közvetlenül az ütközés előtt és után. A lemezek végig rögzítettek, nem mozdulnak el. Hosszú idő után a korong ,,állandósult'' mozgást fog végezni, a korong viselkedése ismétlődő mozgáshoz tart, melyben a korong v_s sebességét közvetlenül az alsó lemezzel történő ütközés után a következő módon fejezhetjük ki a V feszültséggel:

$\displaystyle v_s=\sqrt{\alpha V^2+\beta}.$

Fejezd ki az $\displaystyle \alpha$ és $\displaystyle \beta$ együtthatókat m, g, $\displaystyle \chi$ , d és $\displaystyle \eta$ felhasználásával! Tételezd fel, hogy az ütközésekkor a korong teljes felülete egyenletesen és egyszerre érinti a lemezeket, és a teljes töltéscsere minden ütközéskor pillanatszerűen történik.

(e) (2,2 pont) Az állandósult állapot elérése után a kondenzátor lemezein keresztülfolyó áram I időátlagát így közelíthetjük: I= $\displaystyle \gamma$ V², ha teljesül a qV $\displaystyle \gg$ mgd feltétel. Fejezd ki a $\displaystyle \gamma$ együtthatót m, $\displaystyle \chi$ , d és $\displaystyle \eta$ segítségével!

(f) (3 pont) Ha az alkalmazott V feszültséget (rendkívül lassan) csökkentjük, akkor elérünk egy olyan V_c kritikus feszültséget, amely alatt az áramkörben hirtelen megszűnik az áram. Határozd meg V_c értékét, és a hozzá tartozó I_c áramot m, g, $\displaystyle \chi$ , d és $\displaystyle \eta$ segítségével! Készíts vázlatos grafikont (melyben összehasonlítod V_c értékét a (c) alkérdésben tárgyalt V_k felemelkedési küszöbértékkel) az áram-feszültség karakterisztikáról, vagyis az I-V függvényről, miközben V először nulláról nagyjából 3V_k-ra növekszik, majd újra nullára csökken.

2. feladat. Felemelkedő ballon

Egy héliummal töltött gumiballon a levegőben magasra emelkedik, olyan régiókba, ahol a nyomás és a hőmérséklet a magasság növekedésével csökken. A következő kérdések tanulmányozásánál tételezzük fel, hogy a ballon a terheléstől függetlenül minden esetben gömbölyű marad, és hanyagoljuk el a terhelés térfogatát. Tegyük fel azt is, hogy a ballonban lévő héliumgáz hőmérséklete mindig azonos a környező levegő hőmérsékletével, és minden gázt kezeljünk ideális gázként. Az univerzális gázállandó R = 8,31 J/mol^.K, és a hélium, illetve a levegő moláris tömege rendre M_H= 4,00^.10^-3 kg/mol, illetve M_A= 28,9^.10^-3 kg/mol. A nehézségi gyorsulás g = 9,8 m/s².

A rész: (a) (1,5 pont) A környező levegő nyomása legyen P, hőmérséklete pedig T. A ballon ,,felületi feszültségének'' következtében a ballon belsejében a nyomás nagyobb a külső nyomásnál. A ballon n mol héliumgázt tartalmaz, és a belsejében a nyomás P+ $\displaystyle \Delta$ P. Határozd meg a ballonra ható felhajtóerőt P és $\displaystyle \Delta$ P függvényében!

(b) (2 pont) Egy szép nyári napon Koreában a levegő T hőmérséklete a tengerszint feletti z magasság függvényében a T(z)=T₀ (1-z/z₀) függvény szerint változott a 0 < z < 15 km tartományban, ahol z₀= 49 km és T₀= 303 K. A tengerszinten a nyomás, illetve a sűrűség értéke P₀= 1,01 ^.10⁵ Pa, illetve $\displaystyle \varrho$ ₀= 1,16 kg/m³ volt. Ebben a magasság tartományban a nyomás a

(2.1)

$\displaystyle P(z)=P_0{(1-z/z_0)}^\eta.$

formulával adható meg. Fejezd ki az $\displaystyle \eta$ kitevőt a z₀, $\displaystyle \varrho$ ₀, P₀ és g paraméterekkel, és határozd meg numerikus értékét két értékes számjegy pontossággal. A nehézségi gyorsulást tekintsd a magasságtól független konstansnak.

B rész: Ha egy gömb alakú, nyújtatlan állapotban r₀ sugarú gumiballont r (> r₀) sugarúra fújunk fel, a gumi megnyúlása miatt a ballon felülete extra rugalmas energiára tesz szert. Egy egyszerű elmélet szerint állandó T hőmérsékleten ennek a rugalmas energiának az értéke

(2.2)

$\displaystyle U=4\,\pi\,r_0^2\kappa\,RT\left(2\lambda^2+\frac{1}{\lambda^4}-3\right),$

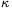ahol a $\displaystyle \lambda$ $\equiv$ r/r₀ ( $\ge$ 1) számértéket lineáris méretnövekedési aránynak nevezzük, a $\kappa$ paraméter pedig egy mol/m² dimenziójú állandó.

(c) (2 pont) Fejezd ki $\Delta$ P-t a (2.2) egyenletben szereplő paraméterek függvényében, és ábrázold vázlatosan a $\Delta$ P nyomáskülönbséget a $\lambda$ =r/r₀ mennyiség függvényében.

(d) (1,5 pont) A 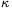$\kappa$ konstans meghatározható a ballon felfújásához szükséges gáz mennyiségéből. A feszítetlen falú ( $\lambda$ =1) ballon T₀=303 K hőmérsékleten és P₀= 1,01 ^.10⁵ Pa nyomáson n₀= 12,5 mol héliumot tartalmaz. Ugyanezen a T₀ hőmérsékleten és P₀ nyomáson a $\lambda$ = 1,5 méretűre felfújt ballon összesen n =3,6^.n₀= 45 mol héliumot tartalmaz. Fejezd ki n, n₀ és $\lambda$ segítségével az a = 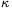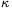$\kappa$ / $\kappa$ ₀ képlettel definiált úgynevezett ,,ballonparamétert'', ahol 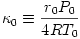$\kappa_0\equiv\frac{r_0P_0}{4RT_0}$ , valamint határozd meg a értékét két értékes számjegy pontossággal.

C rész: A ballont tengerszinten a (d) pontban leírt módon készítjük elő (azaz n =3,6 ^.n₀= 45 mol hélium gázzal $\lambda$ = 1,5 méretűre fújjuk fel T₀= 303 K hőmérsékleten és P₀= 1 atm = 1,01 ^.10⁵ Pa nyomáson). A szerkezet teljes tömege (figyelembe véve a gumiballont, a bezárt gázt és minden egyéb terhet) M_T= 1,12 kg. Ekkor a tengerszintről elengedjük a ballont.

(e) (3 pont) Tegyük fel, hogy a ballon z_f magasságig emelkedik, és ott megáll. Ezen a szinten a felhajtóerő egyensúlyt tart a nehézségi erővel. Határozd meg z_f értékét, valamint ebben a magasságban a $\lambda$ _f paramétert (lineáris méretnövekedési arányt). Válaszodat két értékes jegy pontossággal add meg. A ballon nem sodródik oldalirányban, és nem szökik el belőle gáz.

3. feladat. Atomi erő mikroszkóp

Az atomi erő mikroszkóp (Atomic probe microscope, APM) a nano-tudomány igen hatékony eszköze. Az APM érzékelő karjának elmozdulását egy fotóérzékelő detektálja, az érzékelő karról visszavert lézersugár segítségével, ahogyan a 2. ábrán látható. Az érzékelő kar csak függőleges irányban képes mozogni, és a kar z elmozdulása az idő (t) függvényében a következő differenciálegyenlettel írható le:

(3.1)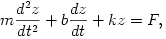

$m\frac{d^2z}{dt^2}+b\frac{dz}{dt}+kz=F,$

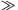ahol m a kar tömege, k=m $\omega$ ₀² az érzékelő kart jellemző rugóállandó, b egy kicsiny csillapítási állandó, melyre teljesül, hogy $\omega$ ₀ $\gg$ (b/m)>0, és végül F a piezoelektromos meghajtó által keltett külső gerjesztő erő.

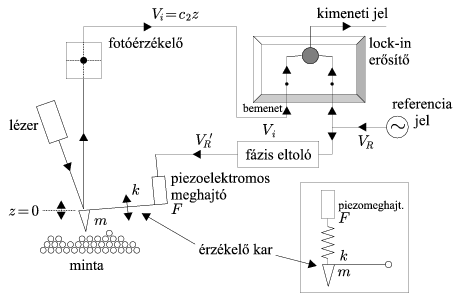
2. ábra. Az atomi erő mikroszkóp (APM) vázlatos rajza. Az ábra jobb alsó sarkában látható kinagyított rész a piezoelektromos meghajtó és az érzékelő kar közti csatolás egyszerűsített mechanikai modelljét mutatja

A rész

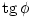(a) (1,5 pont) Ha a gerjesztő erő F=F₀ sin $\omega$ t alakú, akkor a (3.1) egyenlet z(t) megoldása z(t)=Asin ( $\omega$ t- $\phi$ ) alakban írható, ahol A>0 és 0 $\le$ $\phi$ $\le$ $\pi$ . Fejezd ki az A amplitúdót valamint a $\mathop{\rm tg} \phi$ mennyiséget az F₀, m, $\omega$ , $\omega$ ₀ és b paraméter függvényében! Határozd meg az amplitúdót és a $\phi$ fázist az $\omega$ = $\omega$ ₀ rezonanciafrekvencián!

(b) (1 pont) A 2. ábrán szereplő lock-in erősítőben létrejön a bemeneti jelnek és a 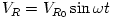$V_R=V_{R_0}\sin\omega t$ úgynevezett lock-in referencia jelnek a szorzata, és az erősítő kimenetén a szorzatnak csak az egyenáramú (DC) komponense jelenik meg. Tegyük föl, hogy a bemeneti jel 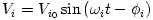$V_i=V_{i_0}\sin\,(\omega_it-\phi_i)$ alakú. Az itt szereplő 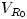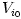$V_{R_0}$ , $V_{i_0}$ , és $\phi$ _i mennyiségek mindegyike adott pozitív állandó. Határozd meg, hogy milyen $\omega$ (>0) frekvencia mellett kapunk nem zérus kimenő jelet! Add meg a nem zérus, egyenáramú (DC) kimenő jel nagyságát leíró formulát ezen a frekvencián!

(c) (1,5 pont) A ,,fázistoló'' egységen átjutó, eredetileg 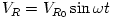$V_R=V_{R_0}\sin\omega t$ alakú lock-in referencia jel alakját a fázistoló egység után a 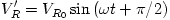$V'_R=V_{R_0} \sin\,(\omega t+\pi/2)$ formula írja le. A V'_R feszültség hatására a piezoelektromos meghajtó az érzékelő kart F=c₁ V'_R erővel gerjeszti. Ezután a fotoérzékelő az érzékelő kar z elmozdulását V_i =c₂ z alakú feszültségjellé alakítja. A formulákban szereplő c₁ és c₂ mennyiségek állandók. Határozd meg a nem zérus, egyenáramú (DC) kimenő jel nagyságát leíró formulát az $\omega$ = $\omega$ ₀ frekvencián!

(d) (2 pont) Az érzékelő kar tömegének kicsiny $\Delta$ m megváltozása $\Delta$ $\omega$ ₀-lal eltolja a rezonanciafrekvenciát. Ennek következtében az eredeti, rezonanciafrekvenciához tartozó $\phi$ fázis is $\Delta$ $\phi$ -vel eltolódik. Határozd meg azt a $\Delta$ m tömeg változást, melynek hatására $\Delta$ $\phi$ = $\pi$ /1800 nagyságú fáziseltolódás jön létre! Tipikusan ilyen nagyságú a fázistolás-mérések pontossága. Az érzékelő kart jellemző fizikai paraméterek értéke a következő: m=1,0^.10^-12 kg, k=1,0 N/m és (b/m)=1,0^.10³ s^-1. 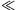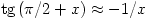Használd az |x| $\ll$ 1 esetén érvényes (1+x)^a $\approx$ 1+ax és $\mathop{\rm tg}\,(\pi/2+x)\approx-1/x$ közelítő formulákat!

B rész

Mostantól kezdve azt az esetet vizsgáljuk, amikor az A részben tárgyalt gerjesztő erőn kívül még az 2. ábrán látható minta is hat valamilyen erővel az érzékelő karra.

(e) (1,5 pont) Annak ismeretében, hogy a minta által kifejtett f(h) erő csak a minta felszíne és az érzékelő kar közti h távolságtól függ, meghatározható az érzékelő kar egyensúlyi helyzetének új h₀ értéke. A h=h₀ érték közelében az erő az f(h) $\approx$ f(h₀)+c₃ (h-h₀) alakban írható fel, ahol c₃ állandó, nem függ h-tól. Fejezd ki az új $\omega$ '₀ rezonanciafrekvenciát $\omega$ ₀, m és c₃ segítségével!

(f) (2,5 pont) A mintát a mikroszkópban vízszintesen mozgatva pásztázzuk a minta felszínét. Az érzékelő kar tűje, melynek töltése Q=6e, egy q=e töltésű, a felszín alatt bizonyos mélységben csapdába került (térben lokalizált) elektron közelébe jut. A csapdázott elektron környékén pásztázva a felszínt, a rezonanciafrekvencia maximálisan észlelhető eltolódása $\Delta$ $\omega$ ₀ (= $\omega$ '₀ - $\omega$ ₀), ami jóval kisebb, mint $\omega$ ₀. Fejezd ki a csapdázott elektron és az érzékelő kar közötti d₀ távolságot maximális frekvencia eltolódás esetén az m, q, Q, $\omega$ ₀, $\Delta$ $\omega$ ₀ mennyiségek és a k_e Coulomb állandó segítségével! Határozd meg d₀ számértékét nm-ben (1 nm = 1^.10^-9 m) $\Delta$ $\omega$ ₀ =20 s^-1 frekvencia eltolódás mellett!

Az érzékelő kar fizikai paraméterei: m= 1,0 ^.10^-12 kg és k=1,0 N/m. Az érzékelő kar tűjében, valamint a minta felületén tekintsünk el a polarizációs effektusoktól. Fizikai állandók: k_e =1/4 $\pi$ $\varepsilon$ ₀ =9,0^.10⁹ N^.m²/C² és e=-1,6^.10^-19 C.

Már regisztráltál?
Új vendég vagy?