Amit jó tudni a kúpszeletekről

II. rész

(A cikk első része lapunk novemberi számában jelent meg.

A kúpszeletek érintőinek érdekes tulajdonságáról szól a következő tétel.

11. tétel. Ha egy külső P pontból érintőket húzunk a kúpszelethez, akkor a P-t az érintési pontokkal összekötő szakaszok a kúpszelet fókuszából vagy egyenlő, vagy pedig egymást 180^o-ra kiegészítő szögekben látszanak. Az utóbbi eset csak akkor fordul elő, ha a kúpszelet hiperbola és a két érintő annak két különböző ágához tartozik.

Bizonyítás. Használjuk a 10. tételben szereplő jelöléseket. A P-n átmenő érintők szerkesztéséből következik, hogy az E₁ és E₂ pontok, illetve az E₁G₁ és E₂G₂ egyenesek egymásnak a P-ből v-re állított m merőleges egyenesre vonatkozó tükörképei, F és E_i pedig egymásnak az e_i egyenesre vonatkozó tükörképei (i=1,2). Ezért a PE_iG_iF négyszögek deltoidok, tehát G_iFP\(\displaystyle \angle\)=G_iE_iP\(\displaystyle \angle\). Így állításunk bizonyításához elég megmutatnunk, hogy vagy G₁E₁P\(\displaystyle \angle\)=G₂E₂P\(\displaystyle \angle\), vagy pedig G₁E₁P\(\displaystyle \angle\)=180^o-G₂E₂P\(\displaystyle \angle\) teljesül.

Parabola esetén a G_i pontok v-nek ugyanazon az oldalán helyezkednek el. Ezért G₁E₁P\(\displaystyle \angle\)=G₂E₂P\(\displaystyle \angle\), mert egymásnak m-re vonatkozó tükörképei (13.(a). ábra).

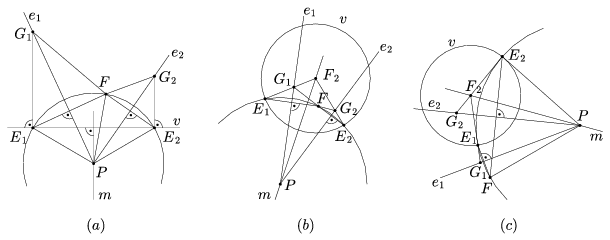
13. ábra

A többi kúpszelet esetén a G_i pont rajta van az F₂E_i egyenesen. Ezért G_iE_iP\(\displaystyle \angle\)=F₂E_iP\(\displaystyle \angle\), ha E_i nincs rajta az F₂G_i szakaszon, és G_iE_iP\(\displaystyle \angle\)=180^o- F₂E_iP\(\displaystyle \angle\), ha E_i rajta van az F₂G_i szakaszon. Mivel F₂E₁P\(\displaystyle \angle\) és F₂E₂P\(\displaystyle \angle\) egymásnak m-re vonatkozó tükörképei, azért a tétel bizonyításához már csak azt kell észrevennünk, hogy az E_i pontok az F₂G_i szakaszokhoz képest csak akkor helyezkednek el különbözőképpen, ha \(\displaystyle \mathcal{K}\) hiperbola, e₁ és e₂ pedig annak két különböző ágához tartozó érintő.  \(\displaystyle \square\)

Következő állításunk hiperbolára csak némi megszorítással igaz, ezért a rövidség kedvéért a hiperbola esetét feladatnak hagyjuk.

12. következmény. Legyen \(\displaystyle \mathcal{K}\) egy hiperbolától különböző kúpszelet, e₁ és e₂ pedig két rögzített érintője. Ekkor \(\displaystyle \mathcal{K}\) tetszőleges érintőjének e₁ és e₂ közé eső szakasza \(\displaystyle \mathcal{K}\) fókuszából állandó szög alatt látszik.

Bizonyítás. Ismét használjuk a 10. tétel jelöléseit, legyen továbbá a tetszőleges érintő e, a rajta lévő érintési pont G₃, az e\(\displaystyle \cap\)e_i pontot pedig jelölje M_i. A 11. tétel szerint G₁FM₁\(\displaystyle \angle\)=G₃FM₁\(\displaystyle \angle\) és G₃FM₂\(\displaystyle \angle\)=G₂FM₂\(\displaystyle \angle\). Vagyis

\(\displaystyle M_1FM_2\sphericalangle=M_1FG_3\sphericalangle+G_3FM_2\sphericalangle=\frac{1}{2} \big(G_1FG_3\sphericalangle+G_3FG_2\sphericalangle\big)=\frac{1}{2}G_1FG_2\sphericalangle, \)

ami viszont állandó, mert G₁ és G₂ rögzített pontok.  \(\displaystyle \square\)

Ha a kúpszelet vezéralakzatát a fókuszból felére kicsinyítjük, akkor a kúpszelet főalakzatát kapjuk. Ez parabola esetén egyenes, a többi esetben kör. Ellipszis és hiperbola esetén a két lehetséges vezérkörből ugyanazt a főkört kapjuk, mert akár v-t kicsinyítjük felére F₂-ből, akár v₁-et F-ből, az eredmény mindkétszer az FF₂ felezőpontja köré írt a sugarú kör.

Ha a fókusznak valamely g egyenesre való tükörképét a fókuszból felére kicsinyítjük, akkor az F-ből g-re állított merőleges talppontját kapjuk. Ezért a 9. következményből azonnal adódik az alábbi tétel.

13. tétel. A kúpszelet fókuszából a kúpszelet tetszőleges érintőjére bocsájtott merőleges talppontja rajta van a főalakzaton.  \(\displaystyle \square\)

Ellipszis esetén a főkör egyik átmérője az ellipszis nagytengelye, s a főkörből merőleges tengelyes affinitással is származtatható az ellipszis (lásd pl. [1] 43. fejezet) (14. ábra).

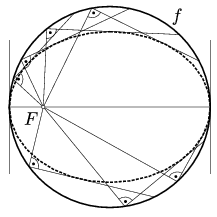
14. ábra

Parabola esetén a főegyenes a parabola tengelyén lévő C parabolapontban érinti a görbét. Ezt a pontot a parabola csúcspontjának, az itteni érintőt pedig a parabola csúcsérintőjének nevezik.

Hiperbola esetén a főkör az aszimptoták szerkesztéséhez nyújt segítséget. A fókuszokból a főkörhöz húzott érintők érintési pontjai az aszimptotákon vannak.

Egyenes és kúpszelet metszéspontja

Az ellipszis, parabola és hiperbola euklidészi értelemben nem szerkeszthetők meg. Azonban tetszőleges egyenessel vett metszéspontjukat meg tudjuk szerkeszteni. Ebben a fejezetben két módszert ismertetünk az F fókuszú, v vezéralakzatú \(\displaystyle \mathcal{K}\) kúpszelet és az e egyenes közös pontjainak a szerkesztésére.

A 6. tétel szerint feladatunk azon k körök középpontjainak megszerkesztése, amelyek átmennek F-en, érintik v-t és merőlegesek e-re. Első módszerünkben az inverziót fogjuk alkalmazni, a másodikban pedig a pont körre vonatkozó hatványának tulajdonságait használjuk fel. Az első módszer alapján a szerkesztés leírása rövid, viszont feltételezzük, hogy az olvasó ismeri az inverzió legfontosabb tulajdonságait. Ezek megtalálhatók pl. [1] 39. fejezetében. A második módszerhez csak középiskolában tanult ismeretek szükségesek, cserében viszont ennek leírása hosszadalmasabb.

A feladat megoldása inverzióval. Alkalmazzunk egy olyan inverziót, melynek pólusa F. Ekkor a szerkesztendő k kör inverz képe valamely k' egyenes lesz, mert k átmegy az inverzió pólusán. Mivel k érinti v-t, azért k' érinti v képét, ami a v' kör (hiszen póluson át nem menő kör vagy egyenes inverz képe kör). Továbbá azt is tudjuk k'-ről, hogy merőleges e inverzére, ami az e' kör vagy egyenes (mert póluson átmenő egyenes inverze egyenes, póluson át nem menő egyenes inverze pedig kör) (15. ábra).

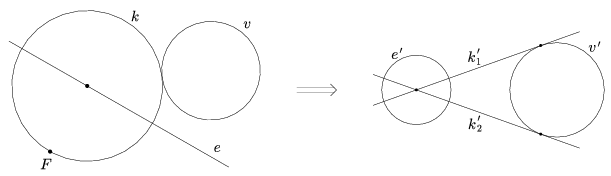
15. ábra

Ezeket felhasználva k'-t egyszerűen megszerkeszthetjük: a v' kör e'-re merőleges érintői lesznek a lehetséges k' egyenesek. Vagyis adott körhöz kell vagy adott ponton (e' középpontján, ha e' kör) átmenő, vagy adott egyenesre (e'-re, ha e' egyenes) merőleges érintőket szerkesztenünk. Az így kapott k' köröket visszainvertálva kapjuk a k köröket, amelyek középpontjai a keresett metszéspontok.

A megoldások száma 2, 1 vagy 0. Ha e' egyenes, akkor e átmegy F-en. Fókuszon átmenő egyenes két pontban metszi a kúpszeletet, kivéve a parabola tengelyével párhuzamos egyenest, amely csak egyben. Ha e' kör, akkor a megoldások száma attól függően 2, 0 vagy 1, hogy középpontja a v' körnek külső- vagy belső pontja, illetve azon rajta lévő pont.

A feladat megoldása inverzió nélkül. Mivel az F ponton átmenő k kör középpontja e-n van, azért k átmegy F-nek e-re vonatkozó F' tükörképén is. (Ha F illeszkedik e-re, azaz F\(\displaystyle \equiv\)F', akkor az FF' egyenes helyett az e-re F-ben állított merőlegest kell tekintenünk.) Feladatunkat ezért átfogalmazhatjuk: olyan kört kell szerkesztenünk, amely átmegy két adott ponton (F-en és F'-n) és érint egy adott kört vagy egyenest (v-t). A szerkesztések leírása megtalálható Horvay Katalin és Reiman István: Geometriai feladatok gyűjteménye I. kötetében ([2], 1332. és 1333. feladatok), a teljesség kedvéért azonban itt is közöljük azokat.

Tekintsük a feladatot megoldottnak. A v-n lévő érintési pontot jelöljük E-vel. Elegendő E-t megszerkesztenünk, mert E,F és F' ismeretében a három ponton átmenő kör szerkeszthető, annak középpontja pedig a keresett pontot adja.

Felhasználunk két lemmát, amelyek szintén megtalálhatók [2]-ben (1324. és 1351.f feladatok).

14. lemma. Ha a P pontból egy körhöz húzott érintőszakasz PE, a P-n átmenő tetszőleges szelő pedig A-ban és B-ben metszi a kört, akkor PE²=PA^.PB.

Bizonyítás. Feltehető, hogy A a PB szakasz belső pontja. PEA\(\displaystyle \angle\)=PBE\(\displaystyle \angle\), mert az EA ívhez tartozó kerületi szögek (16. ábra). A PAE és a PEB háromszögek tehát hasonlóak, mert ezen kívül közös a P-nél lévő szögük is. Így a két háromszögben a megfelelő oldalak aránya megegyezik, \(\displaystyle \frac{PE}{PA}= \frac{PB}{PE}\), amiből adódik a bizonyítandó egyenlőség.  \(\displaystyle \square\)

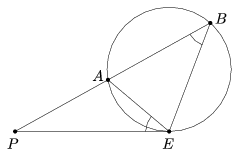
16. ábra

A következő lemma egyúttal eljárást is ad arra, hogy PA és PB ismeretében hogyan szerkesszük meg a \(\displaystyle \sqrt{PA\cdot PB}\) hosszúságú szakaszt.

15. lemma. Ha a P ponton átmenő tetszőleges egyenesre P-től egyik irányba a PA, másik irányba pedig a PB szakaszokat felmérjük, akkor az egyenesre P-ben állított merőleges és AB Thalész-körének E metszéspontjára PE²=PA^.PB.

Bizonyítás. A PAE és a PEB háromszögek hasonlóak, mert P-nél lévő szögük derékszög, továbbá AEP\(\displaystyle \angle\)=EBP\(\displaystyle \angle\), mert merőleges szárú hegyesszögek (17. ábra). Így a két háromszögben a megfelelő oldalak aránya megegyezik, \(\displaystyle \frac{PE}{PA}=\frac{PB}{PE}\), amiből keresztbe szorzással adódik a bizonyítandó egyenlőség.  \(\displaystyle \square\)

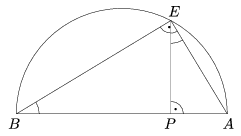
17. ábra

Térjünk vissza a szerkesztéshez. Ha v egyenes, akkor további két alesetet különböztetünk meg. Ha FF' párhuzamos v-vel, akkor E megegyezik FF' szakaszfelező merőlegesének és v-nek a metszéspontjával (18. ábra).

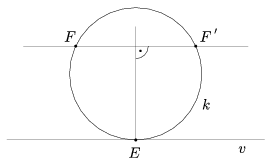
18. ábra

Ha FF' nem párhuzamos v-vel, akkor metszéspontjukat jelöljük H-val. Ekkor a 14. lemma szerint HE²=HF^.HF', s így a 15. lemma alapján HF és HF' szakaszok ismeretében HE hossza megszerkeszthető. Ezután a H középpontú, HE sugarú kör és v metszéspontjai adják a lehetséges E pontokat (19. ábra).

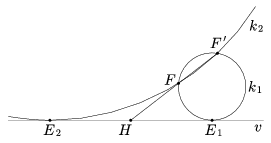
19. ábra

Ha v kör, akkor v-nek és k-nak E-ben közös az érintője. Legyen ez az f egyenes. Vegyünk fel v-n egy tetszőleges T pontot és szerkesszük meg azt az s segédkört, amelyik átmegy F-en, F'-n és T-n. Ha ez érinti v-t, akkor megkaptuk a keresett E pontot. Ha nem érinti, akkor legyen a v-vel alkotott másik metszéspontja T'. Ezután ismét két alesetet különböztetünk meg. Ha FF' párhuzamos TT'-vel, akkor E megegyezik FF' szakaszfelező merőlegesének és v-nek a metszéspontjával, mert ekkor FF' és TT' szakaszfelező merőlegesei egybeesnek és ez az egyenes tartalmazza s-nek is és v-nek is a középpontját (20. ábra).

20. ábra

Ha FF' nem párhuzamos TT'-vel, akkor metszéspontjukat jelöljük H-val. Ekkor HF^.HF'=HE²=HT^.HT', s így a HF és HF' szakaszok ismeretében HE hossza megszerkeszthető. Ezután a H középpontú, HE sugarú kör és v metszéspontjai adják a lehetséges E pontokat (21. ábra). (A H pont nem függ s választásától, TT' mindig ugyanott metszi FF'-t. Ezt itt nem bizonyítjuk, mert a szerkesztéshez nem szükséges. Az érdeklődő olvasó megtalálhatja a bizonyítást [2] 1331. feladatában.)

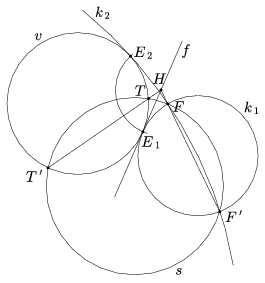
21. ábra

A megoldások számára ebből a szerkesztésből is 2, 1 vagy 0 adódik, hiszen a H középpontú HE sugarú körnek és v-nek 2, 1 vagy 0 közös pontja van.

Irodalom

[1] Hajós György: Bevezetés a geometriába, 6. kiadás, Tankönyvkiadó (Budapest, 1979).

[2] Horvay Katalin és Reiman István: Geometriai feladatok gyűjteménye, I. kötet, 4. kiadás, Tankönyvkiadó (Budapest, 1976).

Kiss György
(A T043556 és T043758 számú OTKA pályázatok támogatásával)