What makes e natural?
This article appeared in the English version of KöMaL, Vol. 2 No. 1, 2004.
When exponential functions and logarithms are presented at school, 2 and 10 seem to be natural choices for the base. A base of 2 is useful because there are several small positive integers whose base-two logarithms are also integers. The advantage of base-ten logarithms, on the other hand, is that even logarithms of numbers of several digits can be compiled in a logarithmic table not longer than a few pages. No matter how natural the bases 2 and 10 may appear, the term ``natural logarithm'' does refer to a base obtained in a seemingly artificial way. This ``artificial'' base is denoted by e, a symbol introduced by the great Swiss mathematician Euler, and its value is approximately e\(\displaystyle \approx\)2.71828182845904523536.
Textbooks usually introduce e as the limit of the sequence \(\displaystyle \left(1+ \frac{1}{n}\right)^{n}\). Sometimes, like Euler himself did, they define it as \(\displaystyle e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\cdots.\) These definitions do not support algebraic operations directly with e. In addition, it is known from the results of Euler, Liouville and Hermite that the number e cannot be accessed as the root of some polynomial of integer coefficients. In other words, e is a transcendental number, like \(\displaystyle \pi\). It is not easy to perform calculations with the number e.
The study of complex functions revealed that the function ex is closely related to trigonometric functions, and thus e is a close relative of \(\displaystyle \pi\). They very often occur together in formulae, for example in Stirling's famous formula establishing \(\displaystyle n! \approx\sqrt{2\pi n}\left(\frac{n}{e}\right)^{n}\).
The number e is natural not because it is easy to calculate with, but because it has special properties that are much more important in mathematical investigations than convenient arithmetical operations. In this paper, we will investigate one - the most important - property of e that is responsible for all the other properties.
A little history of mathematics
In 15th to 16th century Europe, industry, navigation, astronomy and commerce became more and more important and accordingly more and more professional, which was partly due to technological progress but also to mathematical achievements. Since banking required the calculation of compound interest, tables were made (by Simon Stevin, for example). The Swiss Joost Bürgi (1552-1632), who also prepared precision instruments for the market, wanted to create a table that is faster to use than the existing tables for calculating compound interest.
For a given interest rate p, he assigned to the terms of the geometric progression \(\displaystyle \left(1+\frac{p}{100}\right)^{n}\), where n=0,1,2,..., the corresponding term of the arithmetic progression 0, 10, 20, ..., 10n. Thus to the product of any two terms of the original sequence, there is a corresponding term of the arithmetic progression that is obtained by adding the terms assigned to the two terms multiplied. The two sequences were colour-coded in his table (red and black). In present-day notation therefore \(\displaystyle \log_{a}\left(1+\frac{p}{100}\right)^{n}=10n\).
Although he had completed his table by 1611, it was published only nine years later. That is why the Scottish mathematician John Napier could boast the first such table known (1614). Napier's work was based on the approximate description of the motion of someone covering a distance d whose speed at each instant is equal to the remaining distance to be covered (in appropriate units). He divided the time into short intervals of length \(\displaystyle \lambda\), and assumed that the speed was constant within each short interval. He tabulated the corresponding values of distance and time obtained in this way. He coined a name for their relationship out of the Greek words logos (ratio) and arithmos (number). He used a latinized version of his word: logarithm.
In his table, Napier chose \(\displaystyle \lambda\)= 10-7 (and d= 107). In modern terms, we can say that the base of the logarithm in Napier's table was \(\displaystyle \left(1-\frac{1}{10^7}\right)^{10^7}\).
It was Henry Briggs, professor of geometry at Oxford University, who improved Napier's work. One of his goals was to set log 1=0, that is, to make the length of the line segment d equal to unity. He also wanted to obtain the logarithm of 10 as a power of 10. Having considered various options, he decided on log 10=1, which not only meant the birth of decimal logarithm but also the concept of the base of the logarithm being formulated. (Thus if a number is the L-th power of a, then the base-a logarithm of that number is L.)
The number 2.718... is known to have appeared for the first time in the appendix to the English translation of Napier's book called Descriptio. (The appendix was probably written by William Oughtred.) That is where the following statement appeared: loga 10=2.302585 where a\(\displaystyle \approx\)2.71828. Another interesting early achievement is ascribed to Gregory of Saint-Vincent, who calculated the area under the right-angled hyperbola in 1647. He claimed that the area enclosed by the hyperbola of equation xy=1 and the x axis between x=1 and x=e was unity.
Euler used the symbol e first in a manuscript titled Meditatio en experimenta explosione tormentorum nuper instituta in 1727-28. Later on, e appeared in a letter he wrote to Goldbach in 1731. The number e was first printed in 1736, in his paper Mechanica.
As to the origin of the symbol itself, we can all but guess. Some think it is the first letter of the word exponential, others simply see in it the letter following a, b, c, d, the letter most frequently used by contemporary mathematicians. The nasty and jealous say that Euler, of course, named the letter e after himself.
Euler showed that the number e was irrational. In 1844, Liouville proved that it did not occur as a root of any quadratic equation with integer coefficients, and in 1873 Hermite also proved that it was transcendental.
With more and more powerful computers available, more and more digits of e are calculated. The race for the most precise value possible continues to this day. (By 1999, the number of decimal places established reached an order of magnitude of 109.)
The slope of the exponential function
The most interesting and also the most important property of the number e is related to the slope of exponential and logarithm functions.
The graphs of exponential functions of various bases are familiar from school. The function x\(\displaystyle \mapsto\)ax strictly increases if a>1, strictly decreases if 0<a<1 and is a constant if a=1. In each case, the graph is a continuous curve through the point (0,1).
The function is convex for all bases, that is, the line segment connecting any two points of the graph is above the curve (Figure 1).
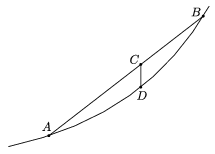
Figure 1
Convexity can also be expressed formally. Let the two endpoints of the line segment be A=(x,ax) and B=(y,ay). Any interior point C of the line segment AB divides AB in some ratio. If the ratio is q:p, where p and q are positive numbers and p+q=1, then the coordinates of C are C=(px+qy,pax+qay), whereas the point D of the graph directly below C is D=(px+qy,apx+qy). Thus the convexity of the exponential function can be written as apx+qy\(\displaystyle \le\)pax+qay for all x, y, p, q (p+q=1, p,q\(\displaystyle \ge\)0).
The convexity of the exponential function can be proved by means of the inequality of weighted arithmetic and geometric means. Actually, the expressions apx+qy and pax+qay are respectively the weighted geometric and arithmetic means of ax and ay, with weights p and q.
The graph of the exponential function has a tangent at every point. (We are stating that without proof now.) It is easily seen that the slope of the tangent depends on the base. Now we will find out what the base should be to make the slope of the tangent drawn at the point (0,1) equal to 1, that is, for what base will the exponential curve touch the line y=x+1. For the time being let us denote the base in question by a.
To obtain close estimates for the number a, we are going to use points of the tangent close to (0,1). Let x be a large positive real number and consider the point \(\displaystyle \left(\frac{1}{x},1+\frac{1}{x}\right)\). Since the curve is convex, the whole tangent is below the graph (except at the point of tangency, see Figure 2). Thus \(\displaystyle a^{\frac{1}{x}\)1+\frac{1}{x}">, and \(\displaystyle \)\left(1+\frac{1}{x}\right)^{x}"> by raising to the x-th power. For another estimate, consider the point \(\displaystyle \left(-\frac{1}{x+1}, 1-\frac{1}{x+1}\right)\). This point is also below the graph, therefore \(\displaystyle a^{-\frac{1}{x+1}\)1-\frac{1}{x+1}">. This time, raising to the power of -(x+1) will reverse the sign since the exponent is negative:
\(\displaystyle a<\left(1-\frac{1}{x+1}\right)^{-(x+1)}= \left(1+\frac{1}{x}\right)^{x+1}. \)
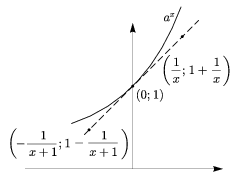
Figure 2
Putting the two estimates together, the base in question must satisfy
\(\displaystyle
\left(1+\frac{1}{x}\right)^{x}
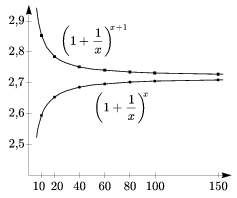
for all x>0. This immediately raises the question: Will we get a closer estimate by substituting a larger number for x? We shall prove that this is indeed the case, the function \(\displaystyle x\mapsto\left(1+\frac{1}{x}\right)^{x}\) strictly increases, whereas the function \(\displaystyle x\mapsto\left(1+\frac{1}{x}\right)^{x+1}\) strictly decreases. Let 0<u<v be arbitrary positive real numbers. We show first that \(\displaystyle
\left(1+\frac{1}{u}\right)^{u}<\left(1+\frac{1}{v}\right)^{v}.
\) Let \(\displaystyle b=\left(1+\frac{1}{u}\right)^{u}\). The graph of the function x\(\displaystyle \mapsto\)bx passes through the point \(\displaystyle U=\left(\frac{1}{u},1+\frac{1}{u}\right)\) (Figure 3). Figure 3 Convexity implies that the point \(\displaystyle V=\left(\frac{1}{v},1+\frac{1}{v}\right)\) is above the graph of the function bx, that is, \(\displaystyle 1+\frac{1}{v\)b^{\frac{1}{v}}">. Taking the v-th powers, \(\displaystyle
b=\left(1+\frac{1}{u}\right)^{u}<\left(1+\frac{1}{v}\right)^{v}.
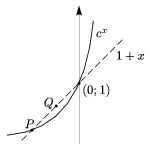
\) Now let \(\displaystyle c=\left(1+\frac{1}{u}\right)^{u+1}\). The graph of the function x\(\displaystyle \mapsto\)cx passes through the point \(\displaystyle P=\left(-\frac{1}{u+1},1-\frac{1}{u+1}\right)\). The point \(\displaystyle Q=\left(-\frac{1}{v+1},1-\frac{1}{v+1}\right)\) is above the graph, therefore \(\displaystyle c^{-\frac{1}{v+1}}<1-\frac{1}{v+1}\). If this is raised to the -(v+1)-th power, the inequality will be reversed, \(\displaystyle c=\left(1+\frac{1}{u}\right)^{u+1}\)\left(1+\frac{1}{v}\right)^{v+1}"> (Figure 4). Figure 4 The monotonicity of each function also can be proved more directly using the inequality of weighted geometric and arithmetic means. For the numbers \(\displaystyle 1+\frac{1}{u}\) and 1, with the weights u and v-u, respectively, we have \(\displaystyle
\left(\left(1+\frac{1}{u}\right)^{u}\cdot1^{v-u}\right)^{\frac{1}{v}}<
\frac{u\cdot\left(1+\frac{1}{u}\right)+(v-u)\cdot1}{v},\) \(\displaystyle \left(1+\frac{1}{u}\right)^{u}<
\left(1+\frac{1}{v}\right)^{v}.
\) Similarly, the inequality of harmonic and geometric means of the same numbers with the weights u+1 and v-u yields \(\displaystyle
\frac{v+1}{\cfrac{u+1}{1+\frac{1}{u}}+\cfrac{v-u}{1}}<
\left(\left(1+\frac{1}{u}\right)^{u+1}\cdot1^{v-u}\right)^{\frac{1}{v+1}},\qquad\left(1+\frac{1}{v}\right)^{v+1}
<\left(1+\frac{1}{u}\right)^{u+1}.
\) The ratio of the increasing lower estimate and decreasing upper estimate clearly tends to 1. Hence the two functions have a common limit at infinity (Figure 5). If that common limit (which we can now denote by e) is chosen as the base of the exponential function, the tangent at (0,1) will indeed enclose an angle of 45o with the x-axis. This is the property of the number e that makes it appear in so many areas of mathematics. Figure 5 The slope at (0,1) is not the only interesting thing about the function ex. The slope at any point (x,ex) is equal to ex, or in other words (ex)'=ex. This is an immediate consequence of the above property. The purpose of this paper has been to show why the limit of the sequence \(\displaystyle \left(1+\frac{1}{n}\right)^{n}\) is so special, why this number is the right choice for the base of the exponential and logarithmic functions. Textbooks, where clarity and precision are essential, usually present the case in a different order. The number e is defined well before tangents and their slopes are mentioned. First it is proved in the section on limits that the sequence \(\displaystyle \left(1+\frac{1}{n}\right)^{n}\) is convergent, and its limit is denoted by e. It is only later, after the introduction of the concepts of the limit of a function and continuity, that the interesting property of the function ex in terms of differentiation becomes apparent. 1. Let n be an arbitrary positive integer. Prove from first principles that \(\displaystyle \left(1+\frac{1}{n}\right)^{n}<3\). 2. Prove that \(\displaystyle
1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\cdots=e.
\) 3. Prove that the function \(\displaystyle \left(1+\frac{a}{x}\right)^{x}\) has a limit at infinity for every real number a. 4. Define the function \(\displaystyle \exp\) as follows: \(\displaystyle \exp\,(a)=\lim_{x\to\infty}
\left(1+\frac{a}{x}\right)^{x}\). Show that \(\displaystyle \exp\,(a+b)=\exp\,(a)\cdot\exp\,
(b)\), and in fact \(\displaystyle \exp\,(a)=e^a\). 5. Prove that \(\displaystyle
e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots\,.
\) A differential operator and a function meet. The operator says, ``Give me your values or I'll differentiate you.'' The function only laughs: ``I'm ex.'' There are a lot of mnemonics to help in memorizing the digits of e. The digits correspond to the number of letters in the words. For example: ``By omnibus I traveled to Brooklyn.'' ``We present a mnemonic to memorize a constant so exciting that Euler exclaimed: `!' when first it was found, yes, loudly `!'. My students perhaps will compute e, use power or Taylor series, an easy summation formula, obvious, clear, elegant!'' (Barel, 1995) [1] Maor, E., e - The History of a Number, Princeton University Press (Princeton, New Jersey, 1994). [2] http://mathworld.wolfram.com/e.html [3] http://www-gap.dcs.st-and.ac.uk/history/HistTopics/e.html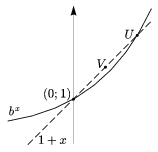
Exercises
In case you haven't yet heard ...
Bibliography
Rita Kós and Géza Kós
