A hajlításról
Ezzel a címmel jelent meg egy tanulságos cikk az akkor már fizikai rovattal is kiegészített Lapok 1959/9. számában. A cikket Vermes Miklós írta, a Fizikai Rovatot Kunfalvi Rezső szerkesztette. Jó barátok voltak, együtt mászták a hegyeket is; mindketten idén lennének 100 évesek. Az alábbi írást az ő emléküknek ajánlom.
*
,,A fűszál meghajlik a szélben, a damaszkuszi penge a vívó kezében. Hajlításra vannak igénybe véve azok a vízszintes gerendák is, amelyeket az egyik végükön befalaztak és másik végükön terhet hordanak. Természetesen a rugalmas lehajlásról van most szó, amikor az alakváltoztató erő megszűnte után a tárgy visszatér eredeti alakjába. Vizsgáljuk meg a hajlítás törvényeit.'' Így kezdődik Vermes Miklós írása. Kiváló invokáció; innen folytassuk!
Tudjuk, hogy a lehajló rúd felső része megnyúlik, az alja összenyomódik, és lesz egy semleges szál, valahol középen, aminek a hossza nem változik meg. Vajon milyen alakú lesz ez a semleges szál? Vékony rúd esetén akár ezt is kérdezhetjük: milyen alakú lesz a lehajló rúd?
Tankönyvekben, még egyetemi tankönyvekben is a lehajló rúd általában körív alakú. Ennek prózai oka van: a rajzoló a legegyszerűbb megoldást választja, a szerző és a lektor pedig simán elfogadja az ábrát, úgysem a meghajlított rúd alakja érdekes, hanem a rúd végének a lehajlása; erre írnak fel, vezetnek le megfelelő formulákat.
Itt most két esetet tárgyalunk. Az egyik, amikor a vízszintesen befogott rúd súlytalan, csak a végét terheljük függőlegesen lefelé irányuló F erővel. Nem erőltetett ez az idealizálás, minden olyan esetben alkalmazható, amikor a rúd végét terhelő F erő sokkal nagyobb, mint a rúd saját súlya. Gondolhatunk akár egy ugródeszkára, amit a műugrók használnak, akár egy horgászbotra, amivel ,,az évszázad fogását'' akarjuk kiemelni a vízből. A KöMaL 2005/2. számának hátoldalán láthatunk egy fényképet a meghajló hurkapálcáról, aminek végét egy vízzel teli nagy tejfölös pohár súlyával terhelte meg a fényképet készítő Kocsis Vilmos. Tessék megfigyelni a pálca alakját! Legjobban a befogásnál görbül, legkevésbé pedig a másik végén, ahol az erő hat - itt szinte kiegyenesedik!
Másik eset az, amikor a vízszintesen befogott rúd a ,,saját súlya alatt'' hajlik meg. Ennek még több alkalmazása van környezetünkben: visszavezethető rá a fák ágainak meghajlásától kezdve a hidak meghajlásáig nagyon sok jelenség. A magasugró vagy rúdugró léc behajlása például úgy tárgyalható, mint a ,,kéttámaszú tartó'' behajlása.
Egy gyümölcsöző analógia
Jól ismert a forgómozgás alapegyenlete, a dinamika forgómozgásra vonatkozó alaptörvénye:
\(\displaystyle M=\Theta\cdot\beta. \)
Jelentése: a testre ható forgatónyomaték és a létrejövő szöggyorsulás arányosak, az arányossági tényező a tehetetlenségi nyomaték.
Formailag ehhez hasonló összefüggést lehet felírni sztatikában, hajlítás esetén:
M=(EI).G.
Jelentése: a meghajlított test adott pontjában ható forgatónyomaték és az adott pontban létrejövő görbület arányosak, az arányossági tényezőt hajlítási merevségnek nevezik. Értéke az E Young-modulus és az I felületi nyomaték szorzata.
Ahogyan a tehetetlenségi nyomaték a testnek az adott tengelyre vonatkozó tömegeloszlásától függ és folytonos tömegeloszlás esetén integrálszámítással határozható meg, ugyanúgy az I felületi nyomaték is a meghajló rúd keresztmetszetének alakjától függ és általában integrálszámítással határozható meg. Ha például a meghajló rúd keresztmetszete a szélességű és b magasságú téglalap, akkor \(\displaystyle I=\frac{1}{12}ab^3\).
További hasonlóság a két összefüggés között, hogy a dinamikai egyenletben szereplő szöggyorsulás a szögelfordulás idő szerinti második deriváltja, míg a sztatikus egyenletben szereplő görbület a lehajló rúd alakját megadó y(x) függvény hely szerinti második deriváltja (legalábbis első közelítésben, kis lehajlás esetén). Éppen ez ad lehetőséget arra, hogy a lehajló rúd alakját meghatározzuk.
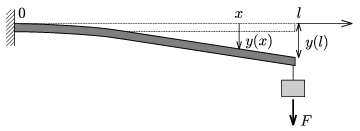
1. ábra
I. eset. Tegyük fel, hogy a vízszintesen befogott rúdnak l hosszúságú darabja áll ki a falból. A rúd súlyától eltekinthetünk, amikor a végére F erő hat függőlegesen lefelé (1. ábra). Ekkor a befogott végétől x távolságra (0\(\displaystyle \le\)x\(\displaystyle \le\)l) lévő pontra vonatkozó forgatónyomaték
M=F(l-x).
Ezek szerint
\(\displaystyle F(l-x)=EI\,\frac{{\rm d}^2y}{{\rm d}x^2}. \)
Ennek a differenciálegyenletnek a megoldását szolgáltató y(x) függvény adja meg a lehajló rúd alakját. Nem is olyan nehéz ezt a függvényt megtalálni. Ha
\(\displaystyle \frac{{\rm d}^2y}{{\rm d}x^2}=\frac{F}{EI}\,(l-x), \)
akkor
\(\displaystyle \frac{{\rm d}y}{{\rm d}x}=\frac{F}{EI}\,\left(lx-\frac{x^2}{2}\right), \)
és hasonló módon
\(\displaystyle y(x)=\frac{F}{EI}\left(l\frac{x^2}{2}-\frac{x^3}{6}\right). \)
Felhasználtuk közben, hogy a befogásnál (x=0-nál) y=0 és az érintő vízszintes: \(\displaystyle \frac{{\rm d}y}{{\rm d}x}=0\).
A lehajló rúd tehát nem körív alakú, se nem parabola alakú, hanem egy harmadfokú görbéből származtatható. Ebből a függvényből megkaphatjuk azt a képlettárakban is szereplő formulát, ami a rúd végének lehajlására vonatkozik:
\(\displaystyle y(l)=\frac{F}{EI}\left(\frac{l^3}{2}-\frac{l^3}{6}\right)=\frac{F}{EI}\,\frac{l^3}{3}. \)
Speciálisan téglalap keresztmetszetű rúdnál: \(\displaystyle I=\frac{1}{12}ab^3\), tehát
\(\displaystyle y(l)=\frac{4F}{EI}\left(\frac{l}{b}\right)^{3}. \)
II. eset. Ha a rúd saját súlya alatti lehajlását vizsgáljuk, akkor azt kell figyelembe vennünk, hogy a rúd adott x pontjára vonatkozó hajlító nyomaték a G összsúlyú rúdnak attól a részétől származik, ami x-től a rúd végéig terjed (2. ábra). Ennek a darabnak a súlya \(\displaystyle G\frac{l-x}{l}\), súlypontja az x helytől \(\displaystyle \frac{l-x}{2}\) távolságra van, tehát az x helyre vonatkozó forgatónyomaték:
\(\displaystyle M=G\frac{l-x}{l}\cdot\frac{l-x}{2}=\frac{G}{2l}{(l-x)}^2. \)
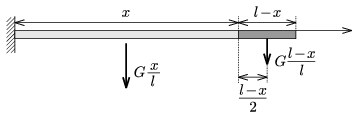
2. ábra
A forgatónyomatékkal arányos görbület most is ott a legnagyobb, ahol (l-x) a legnagyobb, tehát a befogásnál, x=0-nál. Az is igaz marad, hogy a meghajlott rúd görbülete a vége felé haladva nullához tart, a rúd szabad vége mintegy ,,kiegyenesedik''. Az első esethez képest a különbség abban van, hogy a görbület most nem lineárisan, hanem négyzetesen változik a rúd mentén. Ha
\(\displaystyle \frac{{\rm d}^2y}{{\rm d}{x^2}}=\frac{G}{2lEI}\,{(l-x)}^2=\frac{G}{2lEI}\,(l^2-2lx+x^2), \)
akkor
\(\displaystyle \frac{{\rm d}y}{{\rm d}x}=\frac{G}{2lEI}\left(l^2x-lx^2+\frac{x^3}{3}\right), \)
és végül
\(\displaystyle y(x)=\frac{G}{2lEI}\left(l^2\frac{x^2}{2}-l\frac{x^3}{3}+\frac{x^4}{12}\right). \)
Most is felhasználtuk, hogy a befogásnál (x=0-nál) y=0 és az érintő vízszintes: \(\displaystyle \frac{{\rm d}y}{{\rm d}x}=0\).
A saját súlya alatt meghajló rúd alakja tehát egy másod- , egy harmad- és egy negyedfokú ,,parabola'' megfelelő súlyozott keveréke. A rúd végének lehajlása:
\(\displaystyle y(l)=\frac{G}{8EI}\,l^3. \)
Ha téglalap keresztmetszetű rúdról van szó:
\(\displaystyle y(l)=\frac{3}{2}\,\frac{G}{Ea}\left(\frac{l}{b}\right)^{3}. \)
Felhasználhatjuk, hogy G=V\(\displaystyle \varrho\)g=lab\(\displaystyle \varrho\)g, ezzel
\(\displaystyle y(l)=\frac{3}{2}\,\frac{\varrho g}{E}\,\frac{l^4}{b^2}. \)
Érdekes, hogy a lehajlás anyagi minőségtől való függése a \(\displaystyle \frac{\varrho}{E}\) hányadoson keresztül jelenik meg. Például acélra \(\displaystyle E\approx2\cdot10^{11}~\frac{\rm N}{\rm m^2}\) és \(\displaystyle \varrho\approx7{,}8\cdot10^{3}~\frac{\rm kg}{\rm m^3}\), míg fenyőfára \(\displaystyle E\approx10^{10}~\frac{\rm N}{\rm m^2}\) és \(\displaystyle \varrho\approx0{,}5\cdot10^{3}~\frac{\rm kg}{\rm m^3}\), vagyis a \(\displaystyle \frac{\varrho}{E}\) hányados acélra alig tér el a fenyőfára érvényes értéktől. Az azonos keresztmetszetű és hosszúságú acélrúd tehát nagyjából ugyanúgy hajlik le a saját súlya alatt, mint a fenyőfából készült rúd. A különbség majd akkor jelentkezik, ha külső erő terheli a rudakat.
Sok érdekes következménye van még a most levezetett formuláknak, a lehajló rúd alakjára kapott összefüggéseknek; az Olvasó maga is felfedezhet néhányat. Befejezésül álljon itt az a probléma, melyet Vermes Miklós vetett fel az említett cikk végén: ,,Érdekes annak a gerendának a lehajlása, amelynek keresztmetszete ékalakúan vékonyodik a vége felé...''. Vajon ekkor milyen alakú lesz a saját súlya alatt meghajló gerenda? Szinte látom, ahogy Vermes és Kunfalvi összekacsintottak: erre a hegyre nem lesz könnyű felmászni, de biztosan lesz olyan, akinek sikerül!
Radnai Gyula

