Gálfi László: Hőfelvétel vagy hőleadás?

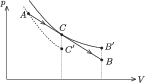
Elég ritkán, de azért találkozunk olyan hőtani körfolyamatot vizsgáló feladattal, amelyben a körfolyamat egyik (nem izotermikus, nem adiabatikus) szakaszán a gáz térfogata nő, nyomása csökken (Lásd például a jelen számunkban kitűzött P. 4160. számú feladatot!). Ilyen például az 1. ábrán látható, a $p-V$ diagramon $AB$ egyenes szakasszal megadott folyamat.

1. ábra

Ilyen esetekben az okozza a nehézséget, hogy meg kell határoznunk: a szakasz melyik részén vesz fel, és melyiken ad le hőt a gáz. Tegyük fel, hogy a szakasz a $C$ pontban érint egy $pV^\kappa= \text{állandó}$ egyenlettel megadható adiabatát. Belátjuk, hogy a gáz az $AC$ szakaszon felvesz, a $CB$ szakaszon lead hőt.

Rajzoljuk meg az $A$ ponton átmenő adiabatát, ennek $C'$ pontjában ugyanakkora a gáz térfogata, mint a $C$ pontban. Az $AC'$ úton nincs hőfelvétel (se hőleadás), a gáz munkát végez, hőmérséklete (belső energiája) tehát csökken. Az $AC$ úton a munkavégzés (a görbe alatti terület) nagyobb, mint az $AC'$ úton, továbbá a gáz hőmérséklete (belső energiája) $C$-ben nagyobb, mint $C'$-ben; ez csak úgy lehetséges, ha a gáz hőt vesz fel az $AC$ szakaszon.

Tekintsük most a $C$-n átmenő adiabata $CB'$ szakaszát; $B'$-ben és $B$-ben a gáz térfogata ugyanakkora. A $CB'$ úton hőfelvétel (hőleadás) nincs, a munkavégzés nagyobb, mint a $CB$ úton, a gáz hőmérséklete (belső energiája) pedig $B$-ben kisebb, mint $B'$-ben. Ez csak úgy lehetséges, hogy a gáz a $CB$ szakaszon hőt ad le.

2. ábra

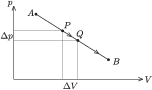
Végezzünk egy kis számítást is! Legyen az $A$-n és $B$-n átmenő egyenes egyenlete (lásd a 2. ábrát) $$p=p_{0}-a\cdot V \qquad (a>0),$$ azaz $$\frac{\Delta p}{\Delta V}=-a.$$ A munkavégzés a $PQ$ szakaszon $$\left(p+\frac{\Delta p}{2}\right) \Delta V,$$ ami nagyon kis változás esetén (a másodrendűen kicsi tag elhagyásával) $p\cdot\Delta V$-vel közelíthető. A belső energia megváltozása: $$\begin{align*} \Delta E & = \frac{f}{2}\, nR \,\Delta T= \frac{f}{2}\,nR\,\Delta \left(\frac{pV}{nR}\right)= \frac{f}{2}\, \left(p\,\Delta V+V\,\Delta p\right)= \frac{f}{2}\, \left(p\,\Delta V-aV\,\Delta V\right)=\\[3pt] &= \frac{f}{2}\, (p-aV)\Delta V, \end{align*}$$ ahol $n$ a gáz mólszáma.

A hőtan első főtétele szerint a gáz által felvett hő: $$Q=\Delta E+p\Delta V=\Delta V \left[\frac{f}{2}(p-aV)+p \right].$$ Ha $Q>0$, azaz $\frac{f}{2}(p-aV)+p >0$, akkor a gáz hőt vesz fel. Rendezve ezt az egyenlőtlenséget azt kapjuk, hogy a hőfelvétel feltétele: $$\frac{f+2}{f}\cdot \frac{p}{V}>a.$$ Ideális gázra $\kappa=\frac{c_{p}}{c_{V}}=\frac{f+2}{f}$, így a táguló gáz hőfelvételének feltételeként a $$\kappa\,\frac{p}{V}>a$$ egyenlőtlenséghez jutottunk. Az adiabata egyenlete $pV^\kappa=$állandó, ennek meredeksége $-\kappa \frac{p}{V}$. (Ezt differenciálszámítás segítségével láthatjuk be, vagy abból a megfontolásból, hogy az adiabata mentén nincs hőfelvétel (se hőleadás), tehát a fentebb levezetett egyenlőtlenség az adiabata mentén haladva egyenlőségbe megy át.)

Ha tehát az állapotváltozást a $p-V$ diagramon megadó egyenes valamely pontjában az ottani adiabata meredeksége kisebb, mint az egyenes meredeksége, akkor a pont környezetében a növekvő térfogatú gáz hőt vesz fel, a csökkenő térfogatú hőt ad le.